1.3 Övningar till Polynom i faktorform
| Teori | Övningar |
G-övningar: 1-6
Övning 1
Om
- \[ x^3 - 5\,x^2 + 12\,x - 6 = (x-2) \cdot {\rm (ett\ polynom)} \]
vad är då graden till det okända polynomet?
Övning 2
Vi har:
- \[ 4\,x^2 + 16\,x - 8 = (x+3) \cdot {\rm (ett\ polynom)} \]
a) Vad är graden till det okända polynomet?
b) Vad är koefficienten till x-termen i det okända polynomet?
Övning 3
Ange ett polynom i faktorform vars nollställen är:
a) 2 och 6
b) -2, och -6
c) 1, -5 och 4
Övning 4
Ange nollställen till följande polynom:
a) \( (x-2) \cdot (x+1) \)
b) \( (3\,x-1) \cdot (2\,x+1) \)
Övning 5
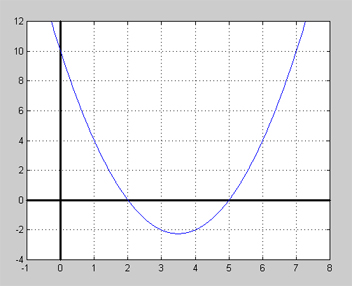
Grafen till en polynomfunktion ser ut så här:
a) Ange några exempel på polynom i faktorform vars nollställen är identiska med kurvans nollställen.
b) Ange det polynom i faktorform vars graf är kurvan ovan.
Övning 6
Faktorisera följande polynom och kontrollera dina svar genom utveckling av de erhållna resultaten:
a) \( x^2 - 6\,x + 8 \)
b) \( 3\,x^2 + 3\,x - 6 \)
c) \( 4\,x^2 - 36 \)
VG-övningar: 7-10
Övning 7
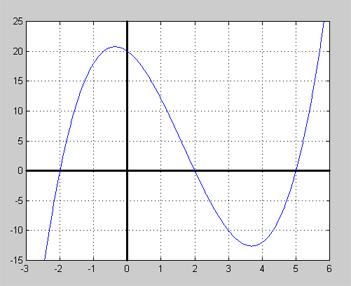
Grafen till en polynomfunktion ser ut så här:
Ange det polynom i faktorform vars graf är kurvan ovan.
Övning 8
Faktorisera följande polynom och kontrollera dina svar genom utveckling av de erhållna resultaten. Ange slutresultaten med heltalskoefficienter.
a) \( 9\,x^2 - 6\,x + 1 \)
b) \( x^2 + 4\,x - 4 \)
c) \( 49\,z^2 + 14\,z + 1 \)
Övning 9
Ange den fullständiga faktoriseringen av polynomet
- \[ x^3 - 9\,x^2 + 26\,x - 24 \]
om en av faktorerna är \((x-4)\).
Övning 10
Två polynom är givna\[ P(x) = 2\,a \cdot x + 3\,a - 4\,b \]
\( Q(x) = 4 \cdot x - 6 \)
För vilka värden av \( a\, \) och \( b\, \) är \( P(x) = Q(x)\, \)?
MVG-övningar: 11-12
Övning 11
Följande 2:a gradspolynom är givet:
\[ P(x) = x^2 - 10\,x + 16 \]
a) Utveckla uttrycket \( Q(x) = (x - a) \cdot (x - b) \) till ett polynom. Bestäm \( a\, \) och \( b\, \) så att \( P(x) = Q(x)\, \). Använd jämförelse av koefficienter.
b) Visa att de värden du får för \( a\, \) och \( b\, \) i a)-delen är lösningar till 2:a gradsekvationen:
\[ x^2 - 10\,x + 16 = 0 \]
Övning 12
Visa att 2:a gradspolynomet \( P(x) = 8\,x^2 + 7\,x - 1 \) kan skrivas som
\[ (a\,x + b) \cdot (c\,x + d) \]
vilket innebär en faktorisering av polynomet \( P(x)\, \). Bestäm a, b, c och d genom att:
a) Hitta först polynomet \( P(x)\, \):s rötter \( x_1\, \) och \( x_2\, \) exakt, dvs bibehåll bråkformen.
b) Sätt sedan \( P(x) = k \cdot (x - x_1) \cdot (x - x_2) \) och bestäm k genom jämförelse av koefficienter. Ange a, b, c och d.
 Hämtar...
Hämtar...