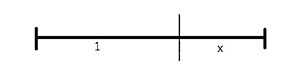Skillnad mellan versioner av "1.5 Övningar till Kontinuerliga och diskreta funktioner"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 117: | Rad 117: | ||
b) En sträcka kan delas i två delar där den längre delen är <math> \, 1 \, </math> och den kortare delen är <math> x\, </math>: | b) En sträcka kan delas i två delar där den längre delen är <math> \, 1 \, </math> och den kortare delen är <math> x\, </math>: | ||
| − | [[Image: Övn 6 60a.jpg]] | + | ::::[[Image: Övn 6 60a.jpg]] |
| − | Om delningen är vald så att hela sträckan förhåller sig till den längre delen som denna bit förhåller sig till den kortare delen, så sägs sträckan vara delad enligt [http://www.svtplay.se/klipp/1678546/det-gyllene-snittet <strong><span style="color: | + | Om delningen är vald så att hela sträckan förhåller sig till den längre delen som denna bit förhåller sig till den kortare delen, så sägs sträckan vara delad enligt [http://www.svtplay.se/klipp/1678546/det-gyllene-snittet <strong><span style="color:blue">gyllene snittet</span></strong>]. Översatt till ekvation blir det: |
::::<math> {\color{White} x} {1+x \over 1} \, = \, {1 \over x} </math> | ::::<math> {\color{White} x} {1+x \over 1} \, = \, {1 \over x} </math> | ||
Versionen från 16 maj 2015 kl. 19.46
| <-- Förra avsnitt | Genomgång | Övningar | Fördjupning | Diagnosprov kap 1 --> |
E-övningar: 1-5
Övning 1
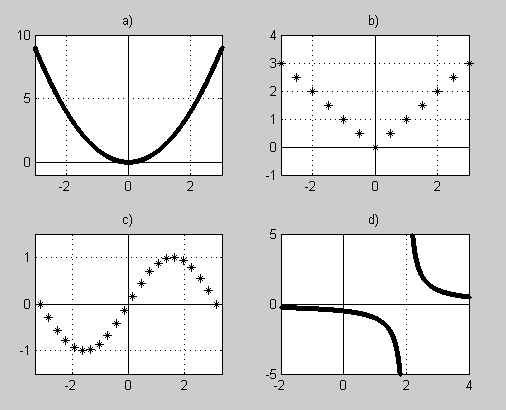
Bestäm för varje graf om den visar en diskret eller en kontinuerlig funktion.
Ange även om och i så fall för vilka \( x \, \) funktionerna har diskontinuiteter.
Motivera dina svar.
Övning 2
a) Rita grafen till den diskreta funktionen
- \[ y = x^2\, \]
vars definitionsmängd är alla heltal \( x\, \) mellan \( -5\, \) och \( 5\, \) dvs \( -5 \leq x \leq 5 \).
Undersök om din grafräknare kan rita diskreta funktioner. Om ja gör det, annars rita manuellt på rutat papper.
b) Rita med grafräknaren grafen till den kontinuerliga funktionen
- \[ y = x^2\, \]
vars definitionsmängd är alla reella tal \( x\, \) mellan \( -5\, \) och \( 5\, \) dvs \( -5 \leq x \leq 5 \).
Fundera själv vilka min- och max-värden du borde ange för räknarens display (WINDOW-knappen).
Övning 3
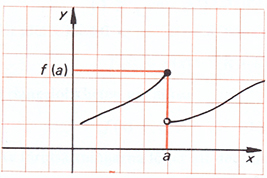
På bilden visas grafen till en funktion. Den ihåliga ringen i grafen betyder att detta värde inte tillhör funktionens värdemängd, medan den ifyllda ringen innebär att detta värde tillhör värdemängden. Anta att varje ruta i grafen har längdenheten \( 1\, \).
a) Är funktionen \( f(x)\, \) diskret eller kontinuerlig?
b) Vilket värde kan du läsa av från grafen för funktionen \( f(x)\, \) för \( x = 4\, \)?
c) För vilka \( x\, \) är funktionen \( f(x)\, \) inte definierad i det ritade intervallet?
d) För vilka \( x\, \) är funktionen \( f(x)\, \) inte kontinuerlig i det ritade intervallet?
Motivera dina svar.
Övning 4
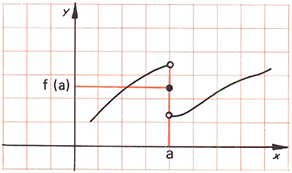
Kom ihåg att de ihåliga ringarna i grafen nedan betyder att dessa värden inte tillhör funktionens värdemängd, medan den ifyllda ringen innebär att detta värde tillhör värdemängden. Anta att varje ruta i grafen nedan har längdenheten \( 1\, \).
a) Vilket värde kan du läsa av från grafen för funktionen \( f(x)\, \) för \( x = 4\, \)?
b) Är funktionen \( f(x)\, \) definierad för alla \( x\, \) i det ritade intervallet?
c) Är funktionen \( f(x)\, \) kontinuerlig för alla \( x\, \) i det ritade intervallet?
d) För vilka \( x\, \) är funktionen \( f(x)\, \) kontinuerlig och för vilka är den diskontinuerlig?.
Motivera dina svar.
Övning 5
I genomgången beräknades de \( \, 12 \, \) första fibonaccitalen. Ta reda på de två första fibonaccitalen och använd mönstret att summan av två på varandra följande fibonaccital ger nästa fibonaccital.
a) Komplettera med miniräknaren beräkningen med ytterligare \( \, 12 \, \) fibonaccital, dvs beräkna \( \, F(13) - F(24) \). Hur många kaninpar kommer att finnas om två år?
b) I genomgången visades grafen för de 12 första fibonaccitalen. Rita Fibonaccis diskreta funktion för fibonaccitalen \( F(12) - F(24) \).
Undersök om din grafräknare kan rita diskreta funktioner. Om ja gör det, annars rita manuellt på rutat papper
C-övningar: 6-8
Övning 6
Använd Excel för att beräkna de första \( \, 24 \, \) fibonaccitalen \( \, F(n), \quad n = 1, 2, 3, \cdots , 24 \). Följ algoritmen som visades på genomgången.
Fortsätt i Excel med att i en 3:e kolumn beräkna kvoten \( \displaystyle {F(n-1) \over F(n)} \) för varje \( \, n = 1, 2, 3, \cdots , 24 \).
a) Mot vilket värde går kvoten \( \displaystyle {F(n-1) \over F(n)} \, \) när \( n\, \) växer? Ange svaret med \( \, 9 \, \) decimaler.
Det värde du har hittat för kvoten ovan är ett närmevärde till det s.k. gyllene snittets proportionella förhållande (skala). Lös b) för att få reda på vad detta innebär:
b) En sträcka kan delas i två delar där den längre delen är \( \, 1 \, \) och den kortare delen är \( x\, \):
Om delningen är vald så att hela sträckan förhåller sig till den längre delen som denna bit förhåller sig till den kortare delen, så sägs sträckan vara delad enligt gyllene snittet. Översatt till ekvation blir det:
- \[ {\color{White} x} {1+x \over 1} \, = \, {1 \over x} \]
Lös denna ekvation exakt. Ange dess positiva lösning - kallad \( g\, \) (= gyllene snittet) samt ett närmevärde till \( g\, \) med nio decimaler. Jämför resultatet med a).
c) Hur skulle man kunna matematiskt beskriva sambandet mellan fibonaccitalen och gyllene snittet?
Övning 7
Rita graferna till följande funktioner.
Avgör om funktionerna är kontinuerliga för alla reella \( x\, \). Om inte, ange för vilka \( x\, \) de är diskontinuerliga samt diskontuiteternas typ. Motivera dina svar.
a) \( f(x) = \) \( {x^2\,-\,3\,x\,-\,4 \over x\,-\,2} \)
b) \( g(x) \, = \, \begin{cases} 3\,x - 2 & \mbox{om } x \leq 0 \\
-2 & \mbox{om } x > 0 \\
\end{cases}
\)
c) \( h(x) \, = \, \begin{cases} 2\,x + 1 & \mbox{om } x \leq 1 \\
5 & \mbox{om } x > 1 \\
\end{cases}
\)
Övning 8
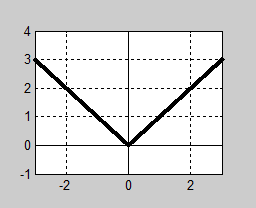
Följande graf till en funktion \( y = f(x)\, \) är given:
a) Ställ upp ett funktionsuttryck för \( f(x)\, \).
Utnyttja möjligheten att för en och samma funktion ställa upp olika uttryck i olika delar av funktionens definitionsmängd.
b) Undersök med hjälp av den allmänna definitionen för kontinuerliga funktioner om \( f(x)\, \) är kontinuerlig för \( x = 0\, \).
A-övningar: 9-11
Övning 9
Följande funktion är given:
- \[ y = f(x) = {x^2 - 9 \over x-3}\;,\qquad x\quad\text{reell} \]
a) Rita funktionens graf. Kan man av grafen dra slutsatsen att \( f(x)\, \) är kontinuerlig för alla \( \,x\)? Om inte, ange för vilka \( x\, \) funktionen är diskontinuerlig. Motivera ditt svar.
b) Faktorisera polynomet i funktionsuttryckets täljare. Förkorta sedan.
c) Är resultatet i b) ett uttryck till en ny funktion eller är det bara en annan form till funktionen \( f(x)\, \)? Motivera ditt svar.
Övning 10
Följande funktion är given:
- \[ y = f(x) = {3\,x^2 + 12\,x + 12 \over x^2\,-\,4}\;,\qquad x\quad\text{reellt tal} \]
a) Ange funktionens diskontinuiteter. Vilka är hävbara och vilka är icke-hävbara diskontinuiteter?
b) Definiera funktionen \(\,f(x)\):s kontinuerliga fortsättning \( g(x)\, \), dvs en funktion som inte längre har \(\, f(x)\):s hävbara diskontinuitet, men är annars identisk med \( f(x)\, \).
c) Rita graferna till \( f(x)\, \) och \( g(x)\, \). Vilka slutsatser kan man dra av grafernas förlopp?
Övning 11
Fibonaccis funktion
- \[ F(n) \, = \, \begin{cases} 1 & \mbox{om } n = 1 \\ 1 & \mbox{om } n = 2\; , \qquad\qquad n \quad\mbox{heltal} \\ F(n-1) + F(n-2) & \mbox{om } n = 3,\,4,\,5,\,\cdots \end{cases} \]
är inte bara diskret utan också rekursiv, vilket betyder att den i sin definition använder sig själv, närmare bestämt de två föregående värdena. Dvs den anropar sig själv fast med olika argument. Man måste alltid känna till de två föregående värdena. Därför har den också två startvärden.
Men det finns även en icke-rekursiv formel för direkt beräkning av fibonaccitalen. Fördelen med denna explicita formel är att man inte behöver känna till några föregående värden. Därför lämpar den sig för direkt beräkning av stora fibonaccital, utan att beräkna alla föregående fibonaccital. Den upptäcktes först 1718 och ser ut så här:
- \[ F(n) = {1\over\sqrt{5}}\,\left({1+\sqrt{5}\over 2}\right)^n\,-\;{1\over\sqrt{5}}\,\left({1-\sqrt{5}\over 2}\right)^n\; , \qquad n \;\mbox{heltal } \geq 1 \]
Bevisa denna explicita formel dvs visa att den uppfyller Fibonaccis rekursionsformel ovan.
Copyright © 2011-2015 Math Online Sweden AB. All Rights Reserved.
 Hämtar...
Hämtar...