Grafritning och ekvationslösning med räknare
| << Repetitioner | Genomgång | 1.1 Polynom >> |
Exempel
Simhopp från \( 10\)-meterstorn - del 1
Marie tävlar i simhopp från \( 10\)-meterstorn. Hennes hopp följer en bana som beskrivs av:
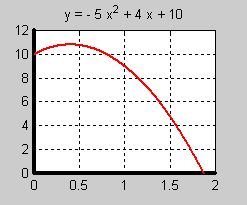
- \[ y = - 5\,x^2 + 4\,x + 10 \]
där \( \;\quad x \, = \, {\rm Tiden\;i\;sekunder\;efter\;hon\;lämnat\;brädan} \)
- \[ y \, = \, {\rm Hennes\;höjd\;över\;vattnet\;i\;meter} \]
a) Rita grafen till funktionen som beskriver Maries hopp i din räknare.
b) När slår Marie i vattnet? Ange svaret med \( \, 10 \, \) decimaler.
- Använd din räknares ekvationslösare för att bestämma polynomets nollställe,
- dvs lösa 2:a gradsekvationen: \( \qquad - 5\,x^2 + 4\,x + 10 = 0 \)
Lösning
a) Beskrivningen som ges här bygger på grafräknaren TI-82 STATS, men kan med lite modifikation tillämpas på alla grafräknare.
Grafritning med miniräknare
|
Så här ritar vi i grafräknaren grafen till funktionen \( \qquad\qquad y = - 5\,x^2 + 4\,x + 10 \) Tryck på knappen Y= och skriv in funktions- uttrycket där markören står: Y1=(-)5X^2+4X+10 Tryck på knappen ENTER och sedan på GRAPH. Ser du grafen till höger är det OK, annars tryck på knappen WINDOW. |
 |
Mata in följande min-/max-värden samt skala för din räknares display (WINDOW):
|
|
|
Tryck på knappen GRAPH igen.
Läs av kurvans skärningspunkt med \( \, x\)-axeln: ungefär \( \, 1,9 \, \).
\( \, y \, \) är \( \, 0 \, \) när \( \, \underline{x\, \approx 1,9\,} \): Funktionens nollställe.
Simhopp från \( 10 \)-meterstorn - del 2
Värdena i a) för WINDOW:s \( \, min \, \), \( \, max \, \) och \( \, scl \, \) kan man i regel få fram genom att prova sig fram flera gånger. Men:
Vill du veta hur man matematiskt får fram dem, läs här:
Hämtar...
b) Vi kan nu använda närmevärdet från a) som startvärde för kalkylatorns ekvationslösare som kommer att precisera nollstället.
Ekvationslösning med miniräknare
När "exakt" slår Marie i vattnet? Lös ekvationen \( \; - 5\,x^2 + 4\,x + 10 = 0 \; \) med \( \, 10 \, \) decimalers noggrannhet.
- Tryck i miniräknaren på knappen MATH.
- Gå med piltangenten till Solver...
- Tryck på ENTER.
- Mata in ekvationens vänsterled där markören står, så att det efteråt står följande två rader i displayen:
- EQUATION SOLVER
- eqn:0=(-)5X^2+4X+10
- Tryck först på knappen ALPHA (orange) och sedan på SOLVE (i orange ovanpå ENTER).
Mata in startvärdet \( \, x\, \approx 1,9 \, \) som vi fick fram i a) och tryck en gång till på först ALPHA och sedan SOLVE.
Värdet \( \, x = 1,8696938456\ldots \, \) visas i displayen vilket betyder:
Marie slår i vattnet efter \( \underline{1,8696938456\ldots\,\,{\rm sek}}\): Ekvationens lösning.
Copyright © 2019 TechPages AB. All Rights Reserved.
