2.2 Genomsnittlig förändringshastighet

<<  Förra avsnitt

Genomgång

Övningar

Nästa demoavsnitt  >>

Lektion 13: Genomsnittlig förändringshastighet

Tre exempel på genomsnittlig förändringshastighet

Exempel 1 Marginalskatt

Martins månadslön höjs från \( \, 23\;000 \, \) kr till \( \, 24\;200 \, \) kr.

I Skatteverkets skattetabell för 2015 (tabell 29, kolumn 2) hittar vi \( \, 5\;297 \, \) kr skatt för den gamla och \( \, 5\;676 \, \) kr skatt för den nya lönen.

Beräkna marginalskatten som är den procentuella andelen av varje lönehöjning som går till skatt.

Matematiskt är marginalskatten skattens genomsnittliga förändringshastighet när skatten uppfattas som en funktion av lönen.

Lösning: Skatten som en funktion av lönen: \( x\, \) \( y\, \) \( 23\,000 \) \( 5\,297\) \( 24\,200 \) \( 5\,676 \)

\( x \, = \, {\rm Månadslönen\;i\;kr} \) \( y \, = \, {\rm Skatten\;i\;kr} \)

\( \qquad\qquad \)

Fil:Diskret loneSkattfkt 40.jpg

Kvoten mellan skattehöjning och lönehöjning (lutningen i figuren ovan) kallas för funktionen \( \, y\):s genomsnittliga förändringshastighet:

\[ {\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} = {{\rm Skattehöjningen} \over {\rm Lönehöjningen}} = {5\,676 - 5\,297 \over 24\,200 - 23\,000} \; = \; {379 \over 1200} \; = \; {\color{Red} {0,316}} \; = \; 31,6 \, \%\]

I intervallet \( \; 23\,000 \,\leq\, x \,\leq\, 24\,200 \, \) har funktionen \( \, y \, \) den genomsnittliga förändringshastigheten \( \; {\color{Red} {0,316}} \).

Dvs \( \, y \, \) växer i detta intervall med \( {\color{Red} {0,316}} \; y\)-enheter per \( x\)-enhet. Med andra ord, marginalskatten är lutningen i figuren ovan.

Ekonomisk tolkning:   Martin måste betala \( \, 31,6\,\) öre i skatt för varje mer intjänad krona. Man säger: marginalskatten är \( \, 31,6 \, \% \).

Vi ersätter nu den diskreta skattefunktionen i tabellform med en kontinuerlig funktion som är given med ett algebraiskt uttryck:

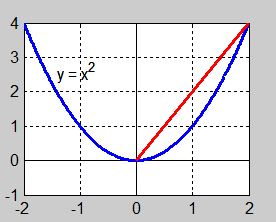
Exempel 2 Kvadratisk funktion

Givet:        Funktionen \( \, y \, = \, f(x) \, = \, x^2 \) Intervallet \( \, 0 \,\leq\, x \,\leq\, 2 \) Sökt:         Funktionens genomsnittliga förändringshastighet i intervallet \( \, 0 \leq x \leq 2 \). Lösning: \[ {\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} \; = \; {f(2) \, - \, f(0) \over 2 - 0} \; = \; {2^2 \, - \, 0^2 \over 2 - 0} \; = \; {4 \, - \, 0 \over 2} \; = \; {4 \over 2} \; = \; {\color{Red} 2} \] I intervallet \( \, 0 \leq x \leq 2 \, \) har funktionen \( \, y = x^2 \, \) den genomsnittliga förändringshastigheten \( \, {\color{Red} 2} \). Dvs funktionen \( \, y = x^2 \, \) växer i detta intervall med \( \, {\color{Red} 2} \; y\)-enheter per \( \, x\)-enhet.

Geometrisk tolkning:    Om man ersätter kurvan \( \, y = x^2 \, \) med en rät linje har denna linje som kallas för kurvans sekant, lutningen \( \, {\color{Red} 2} \).

Sekantens lutning är kurvans genomsnittliga förändringshastighet i intervallet \( \, 0 \leq x \leq 2 \).

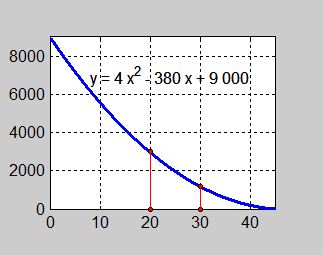
Exempel 3 Oljetank

En oljetank läcker genom ett hål i tankens botten. Utströmningen av oljan beskrivs av funktionen: \[ y \, = \, 4\,x^2 - 380\,x + 9\,000 \] där \( \; \quad \! x \, = \, {\rm Tiden\;i\;minuter} \) \[ y \, = \, {\rm Oljans\;volym\;i\;liter} \] a)    Rita grafen till funktionen som beskriver utströmningen. b)    Hur stor är oljans genomsnittliga utströmningshastighet i hela tidsintervallet        från början tills tanken är tom. c)    Beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet \( \, 20 \leq x \leq 30 \, \).

Lösning:

a)  Se grafen ovan.

b)  Grafen tyder på att tanken kommer att vara tom efter ca. \( \, 45 \, \) minuter.

Den exakta tiden får man genom att sätta volymen \( \, y \, \) till \( \, 0 \, \) dvs genom att lösa 2:a gradsekvationen:

\( \qquad 4\,x^2 - 380\,x + 9\,000 = 0 \qquad \) Räknarens ekvationslösare visar att \( \, x = 45\, \) är även den exakta lösningen.

Därför är hela tidsintervallet från början tills tanken är tom: \( \, 0 \leq x \leq 45 \, \).

I detta intervall är oljans genomsnittliga utströmningshastighet:

\[ {\Delta y \over \Delta x} = {f(45) \, - \, f(0) \over 45 - 0} = {0 \, - \, 9000 \over 45} = {-9000 \over 45} = -200 \]

Dvs i intervallet \( \, 0 \leq x \leq 45 \, \) sjunker oljans volym med \( \, 200 \, \) liter per minut.

c)  Oljans genomsnittliga utströmningshastighet i intervallet \( \, 20 \leq x \leq 30 \, \):

\[ f\,(30) = 4 \cdot 30^2 - 380 \cdot 30 + 9\,000 = 1200 \]

\[ f\,(20) = 4 \cdot 20^2 - 380 \cdot 20 + 9\,000 = 3000 \]

\[ {\Delta y \over \Delta x} = {f(30) \, - \, f(20) \over 30 - 20} = {1200 \, - \, 3000 \over 30 - 20} = {-1800 \over 10} = -180 \]

Dvs i intervallet \( \, 20 \leq x \leq 30 \, \) sjunker oljans volym med \( \, 180 \, \) liter per minut.

Allmän definition

Givet:        Funktionen \( y \, = \, f\,(x) \) i form av en formel, tabell eller graf.

Något intervall på \( x\, \)-axeln med givna gränser \( \, x_1 \, \) och \( \, x_2 \, \) dvs \( \; x_1 \,\leq\, x \,\leq\, x_2 \).

Sökt:         Funktionens genomsnittliga förändringshastighet i intervallet \( \, x_1 \,\leq\, x \,\leq\, x_2 \).

Lösning:     \( \displaystyle{{\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} \; = \; {y_2 - y_1 \over x_2 - x_1} \; = \; {\boxed {f(x_2) \, - \, f(x_1) \over x_2 - x_1}}} \quad {\rm Detta\;uttryck\;har\;använts\;i\;exemplen.} \)

Medan uttrycket ovan lämpar sig i de flesta enkla beräkningssammanhang, används i andra sammanhang, t.ex. när derivatan definieras, en annan variant av det.

Denna variant får vi genom att i uttrycket ovan införa en ny beteckning \( \, h\, \) för intervallets längd:

\[\begin{align} h & = x_2 - x_1 \qquad & | \; + \, x_1 \\ x_1 + h & = x_2 \\ \end{align}\]

Om vi nu i det inramade uttrycket ovan ersätter \( \, x_2 \) med \( \,x_1 + h \) och \( \, x_2 - x_1 \) med \( \, h \), får vi den allmänna definitionen:

Funktionen \( \, y = f\,(x)\):s   genomsnittliga förändringshastighet   i ett intervall av längden \( \, h \, \) är:

\( \quad \displaystyle {{\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h}} \qquad {\rm i\;\;intervallet } \qquad x_1 \,\leq\, x \,\leq\, x_1 + h \)

Observera att den genomsnittliga förändringshastigheten endast kan definieras i ett givet intervall på \( \, x\)-axeln.

Denna definition för genomsnittlig förändringshastighet användes i Aktiviteten och kommer att användas även i fortsättningen i detta kapitel.

Beteckningar

Uttrycket \( \quad \displaystyle {{\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h}} \quad \) har ett antal beteckningar som allihopa är synonymer:

Genomsnittlig förändringshastighet

Förändringskvot

Ändringskvot

Differenskvot

Kärt barn har många namn.

Genomsnittlig vs. momentan förändringshastighet

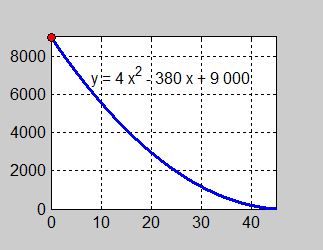
Exempel 3 Oljetank (forts.)

En oljetank läcker genom ett hål i tankens botten enligt: \[ y \, = \, 4\,x^2 - 380\,x + 9\,000 \] där \( \; \quad \! x \, = \, {\rm Tiden\;i\;minuter} \) \[ y \, = \, {\rm Oljans\;volym\;i\;liter} \] När är oljans utströmningshastighet störst? Kan vi beräkna den? Beräkna oljans genomsnittliga utströmningshastighet i intervallet \( \, 0 \,\leq\, x \,\leq\, {\color{Red} {0,1}} \, \). Tolka resultatet.

Lösning:

Fysiken lär oss att utströmningshastigheten är störst när oljan har mest volym och därmed trycket på hålet är sörst, dvs i början.

Även grafen visar att kurvans lutning är störst vid tiden \( \, x = 0\, \) när oljan har den största volymen \( \, 9\,000 \) liter.

Därför är oljans utströmningshastighet störst vid tiden \( \, x = 0 \, \) vilken vi dock inte kan beräkna, därför att det inte finns något \( \, x\)-intervall:

Denna hastighet är inte längre genomsnittlig i något intervall utan ögonblicklig eller momentan. Men vi kan närma oss den.

Oljans genomsnittliga utströmningshastighet i intervallet \( \, 0 \,\leq\, x \,\leq\, {\color{Red} {0,1}} \, \):

\[ f\,({\color{Red} {0,1}}) = 4 \cdot {\color{Red} {0,1}}\,^2 - 380 \cdot {\color{Red} {0,1}} + 9\,000 = 8962,04 \]

\[ {\Delta y \over \Delta x} = {f({\color{Red} {0,1}}) \, - \, f(0) \over {\color{Red} {0,1}} - 0} = {8962,04 \, - \, 9000 \over {\color{Red} {0,1}}} = {-37,96 \over {\color{Red} {0,1}}} = -379,6 \]

I intervallet \( \, 0 \leq x \leq {\color{Red} {0,1}} \, \) sjunker oljans volym med \( 379,6\, \) liter per minut.

Tolkning: Detta är ett närmevärde för den momentana utströmningshastigheten vid tiden \( \, x = 0\, \) (exakta värdet).

Faktiskt är det inget dåligt närmevärde, för det exakta värdet kommer att visa sig vara \( -380 \), se 2.4 Derivatans definition.

För att kunna definiera derivatan behöver vi konceptet Gränsvärde, där man låter intervallets längd gå mot \( \, 0\, \):\( \qquad {\color{Red} {\boxed{h \to 0}}} \)

Internetlänkar

http://www.youtube.com/watch?v=08yI3grz17I

http://www.youtube.com/watch?v=Cze2KrRhHiM

http://www.iceclimbers.net/fil/matematik_c/12.genomsnittlig_forandringshastighet.pdf

http://ingforum.haninge.kth.se/matCD/F%F6rel%E4sning01.pdf

Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.