3.1 Lösning 4c

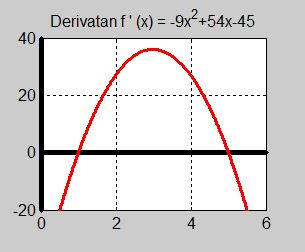
Derivatans graf visar följande:

För alla \( {\color{White} {xxxxxx}} x < 1 {\color{White} x} \) är \(\, f\,'(x) < 0 \). Kurvan ligger under \( \, x\)-axeln.

I intervallet \( {\color{White} x} 1 < x < 5 {\color{White} x} \) är \(\, f\,'(x) > 0 \). Kurvan ligger över \( \, x\)-axeln.

För alla  \( {\color{White} {xxxxxx}} x > 5 {\color{White} x} \) är \(\, f\,'(x) < 0 \). Kurvan ligger under \( \, x\)-axeln.

Slutsats:

För alla \( {\color{White} {xxxxxx}} x < 1 {\color{White} x} \) är \(\, f(x) \) avtagande.

I intervallet \( {\color{White} x} 1 < x < 5 {\color{White} x} \) är \(\, f(x) \) växande.

För alla  \( {\color{White} {xxxxxx}} x > 5 {\color{White} x} \) är \(\, f(x) \) avtagande.