Skillnad mellan versioner av "1.5a Lösning 10c"
Taifun (Diskussion | bidrag) m (moved 1.5a Svar 10c to 1.5a Lösning 10c) |
Taifun (Diskussion | bidrag) m |
||
| Rad 9: | Rad 9: | ||
<math> x_2 = 2 \, {\color{White} xx} </math> är en icke-hävbar diskontinuitet. | <math> x_2 = 2 \, {\color{White} xx} </math> är en icke-hävbar diskontinuitet. | ||
| − | Den hävbara diskontinuiteten <math> x_1 = -2\, </math> ses | + | Den hävbara diskontinuiteten <math> x_1 = -2\, </math> ses inte i grafen till <math> f(x)\, </math>. Men i själva verket finns ett "hål" eller en "lucka" i <math> x = -2\, </math> som man inte ser med blotta ögat. Så funktionen <math> f(x)\, </math> är inte definierad för <math> x = -2\, </math> och har en diskontinuitet där. Den andra, icke-hävbara diskontinuiteten <math> x_2 = 2 \, </math> visas tydligt med ett oändlighetsställe. |
| − | + | Funktionen <math> g(x)\, </math> däremot är både definierad och kontinuerlig för <math> x_1 = -2\, </math>. Det finns "hål" i grafen där. Men även <math> g(x)\, </math> är inte definierad för <math> x_2 = 2 \, </math> och - precis som <math> f(x)\, </math> en icke-hävbar diskontinuitet av typ oändlighetsställe där vilket även ses i grafen. | |
| − | + | ||
| − | + | ||
Versionen från 17 juli 2014 kl. 12.15
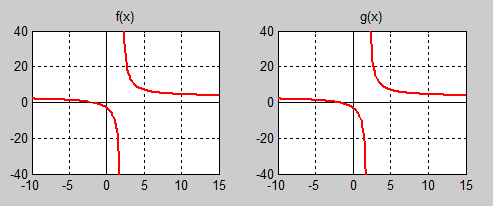
Till synes visar resultatet helt identiska kurvor. Men från övningens a)-del vet vi:
Funktionen \( f(x)\, \) har två diskontinuiteter\[ x_1 = -2 {\color{White} x} \] är en hävbar diskontinuitet.
\( x_2 = 2 \, {\color{White} xx} \) är en icke-hävbar diskontinuitet.
Den hävbara diskontinuiteten \( x_1 = -2\, \) ses inte i grafen till \( f(x)\, \). Men i själva verket finns ett "hål" eller en "lucka" i \( x = -2\, \) som man inte ser med blotta ögat. Så funktionen \( f(x)\, \) är inte definierad för \( x = -2\, \) och har en diskontinuitet där. Den andra, icke-hävbara diskontinuiteten \( x_2 = 2 \, \) visas tydligt med ett oändlighetsställe.
Funktionen \( g(x)\, \) däremot är både definierad och kontinuerlig för \( x_1 = -2\, \). Det finns "hål" i grafen där. Men även \( g(x)\, \) är inte definierad för \( x_2 = 2 \, \) och - precis som \( f(x)\, \) en icke-hävbar diskontinuitet av typ oändlighetsställe där vilket även ses i grafen.