Skillnad mellan versioner av "2.2 Genomsnittlig förändringshastighet"

Från Mathonline
Hoppa till: navigering, sök
m
m
Rad 9: Rad 9:
  
  
−
[[File: Lektion_17_Genomsnittlig_forandringshastighet.pdf|<strong><span style="color:blue">Lektion 17: Genomsnittlig förändringshastighet</span></strong>]]
+
[[Media: Lektion_13_Genomsnittlig_forandringshastighet.pdf|<b><span style="color:blue">Lektion 13: Genomsnittlig förändringshastighet</span></b>]]
−
__NOTOC__
+
 
<big>
 
<big>
 +
<div class="ovnE">
 +
<small>
 +
=== <b><span style="color:#931136">Tre exempel på genomsnittlig förändringshastighet</span></b> ===
 +
<br>
 
<div class="exempel">
 
<div class="exempel">
−
=== <b><span style="color:#931136">Exempel 1 Marginalskatt</span></b> ===
+
==== <b><span style="color:#931136">Exempel 1 Marginalskatt</span></b> ====
 
Martins månadslön höjs från <math> \, 23\;000 \, </math> kr till <math> \, 24\;200 \, </math> kr.
 
Martins månadslön höjs från <math> \, 23\;000 \, </math> kr till <math> \, 24\;200 \, </math> kr.
  
−
I [https://www.skatteverket.se/download/18.3f4496fd14864cc5ac9f637/1424778677969/manadslon_manad.pdf <strong><span style="color:blue">Skatteverkets skattetabell</span></strong>] för 2015 (tabell 29, kolumn 2) hittar vi
+
I [https://www.skatteverket.se/download/18.3f4496fd14864cc5ac9f637/1424778677969/manadslon_manad.pdf <b><span style="color:blue">Skatteverkets skattetabell</span></b>] för 2015 (tabell 29, kolumn 2) hittar vi
  
 
<math> \, 5\;297 \, </math> kr skatt för den gamla och <math> \, 5\;676 \, </math> kr skatt för den nya lönen.
 
<math> \, 5\;297 \, </math> kr skatt för den gamla och <math> \, 5\;676 \, </math> kr skatt för den nya lönen.
Rad 22: Rad 25:
 
Beräkna <b><span style="color:#931136">marginalskatten</span></b> som är skattens procentuella andel i varje mer intjänad krona.
 
Beräkna <b><span style="color:#931136">marginalskatten</span></b> som är skattens procentuella andel i varje mer intjänad krona.
  
−
Matematiskt är marginalskatten skattens <strong><span style="color:red">genomsnittliga förändringshastighet</span></strong> när skatten uppfattas som en <strong><span style="color:red">funktion</span></strong> av lönen.
+
Matematiskt är marginalskatten skattens <b><span style="color:red">genomsnittliga förändringshastighet</span></b> när skatten uppfattas som en <b><span style="color:red">funktion</span></b> av lönen.
  
 
'''Lösning:'''
 
'''Lösning:'''
Rad 46: Rad 49:
 
</tr>
 
</tr>
 
</table>
 
</table>
−
Förhållandet (kvoten) mellan skattehöjning och lönehöjning kallas för funktionen <math> \, y</math>:s <strong><span style="color:red">genomsnittliga förändringshastighet</span></strong>:
+
Förhållandet (kvoten) mellan skattehöjning och lönehöjning kallas för funktionen <math> \, y</math>:s <b><span style="color:red">genomsnittliga förändringshastighet</span></b>:
  
 
:::<math> {\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} = {{\rm Skattehöjningen} \over {\rm Lönehöjningen}} = {5\,676 - 5\,297 \over 24\,200 - 23\,000} \; = \; {379 \over 1200} \; = \; {\color{Red} {0,316}}  \; = \; 31,6 \, \%</math>
 
:::<math> {\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} = {{\rm Skattehöjningen} \over {\rm Lönehöjningen}} = {5\,676 - 5\,297 \over 24\,200 - 23\,000} \; = \; {379 \over 1200} \; = \; {\color{Red} {0,316}}  \; = \; 31,6 \, \%</math>
Rad 52: Rad 55:
 
I intervallet <math> \; 23\,000 \,\leq\, x \,\leq\, 24\,200 \, </math> har funktionen <math> \, y \, </math> den genomsnittliga förändringshastigheten <math> \; {\color{Red} {0,316}} </math>.
 
I intervallet <math> \; 23\,000 \,\leq\, x \,\leq\, 24\,200 \, </math> har funktionen <math> \, y \, </math> den genomsnittliga förändringshastigheten <math> \; {\color{Red} {0,316}} </math>.
  
−
Dvs <math> \, y \, </math> växer i detta intervall med <math> \; {\color{Red} {0,316}} \quad y</math>-enheter per <math> \, x</math>-enhet.
+
Dvs <math> \, y \, </math> växer i detta intervall med <math> {\color{Red} {0,316}} \; y</math>-enheter per <math> x</math>-enhet.
  
 
'''Ekonomisk tolkning''':&nbsp; &nbsp;Martin måste betala <math> \, 31,6\,</math> öre i skatt för varje mer intjänad krona. Man säger: marginalskatten är <math> \, 31,6 \, \% </math>.
 
'''Ekonomisk tolkning''':&nbsp; &nbsp;Martin måste betala <math> \, 31,6\,</math> öre i skatt för varje mer intjänad krona. Man säger: marginalskatten är <math> \, 31,6 \, \% </math>.
Rad 62: Rad 65:
  
 
<div class="exempel">
 
<div class="exempel">
−
=== <b><span style="color:#931136">Exempel 2 Kvadratisk funktion</span></b> ===
+
==== <b><span style="color:#931136">Exempel 2 Kvadratisk funktion</span></b> ====
 
<table>
 
<table>
 
<tr>
 
<tr>
Rad 83: Rad 86:
 
</table>
 
</table>
  
−
'''Geometrisk tolkning''':&nbsp; &nbsp;Om man ersätter kurvan <math> \, y = x^2 \, </math> med en <strong><span style="color:red">rät linje</span></strong> har denna linje som kallas för kurvans <strong><span style="color:red">sekant</span></strong>, lutningen <math> \, {\color{Red} 2} </math>.
+
'''Geometrisk tolkning''': &nbsp;&nbsp; Om man ersätter kurvan <math> \, y = x^2 \, </math> med en <b><span style="color:red">rät linje</span></b> har denna linje som kallas för kurvans <b><span style="color:red">sekant</span></b>, lutningen <math> \, {\color{Red} 2} </math>.
  
−
::::::&nbsp; &nbsp;Sekantens <strong><span style="color:red">lutning</span></strong> är kurvans <strong><span style="color:red">genomsnittliga förändringshastighet</span></strong> i intervallet <math> \, 0 \leq x \leq 2 </math>.  
+
:::::::Sekantens <b><span style="color:red">lutning</span></b> är kurvans <b><span style="color:red">genomsnittliga förändringshastighet</span></b> i intervallet <math> \, 0 \leq x \leq 2 </math>.  
 
</div> <!-- exempel2 -->
 
</div> <!-- exempel2 -->
 +
</small>
  
  
−
== <b><span style="color:#931136">Allmän definition</span></b> ==
+
</div> <!-- "ovnE" -->
−
'''Givet''': &nbsp; &nbsp; &nbsp; &nbsp;Funktionen <math> y \, = \, f\,(x) </math> i form av en formel, tabell eller graf.
+
  
−
:::Något intervall på <math> x\, </math>-axeln med givna gränser <math> \, x_1 \, </math> och <math> \, x_2 \, </math> dvs <math> \; x_1 \,\leq\, x \,\leq\, x_2 </math>.
 
  
−
'''Sökt''': &nbsp; &nbsp; &nbsp; &nbsp; Funktionens genomsnittliga förändringshastighet i intervallet <math> \, x_1 \,\leq\, x \,\leq\, x_2 </math>.
+
<div class="ovnC">
−
 
+
−
'''Lösning''': &nbsp; &nbsp; <math> \displaystyle{{\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} \; = \; {y_2 - y_1 \over x_2 - x_1} \; = \; {f(x_2) \, - \, f(x_1) \over x_2 - x_1}} </math>
+
−
 
+
−
Uttrycket ovan har använts i exemplen <math> \, 1</math>-<math>2 </math>.
+
−
 
+
−
En enklare form på uttrycket får man om man inför den nya beteckningen <math> h\, </math> för intervallets längd:
+
−
 
+
−
::::<math>\begin{align} h & = x_2 - x_1  \qquad  & | \; + \, x_1 \\
+
−
                  x_1 + h & = x_2                                \\
+
−
          \end{align}</math>
+
−
 
+
−
I formeln ovan ersätter vi <math> \, x_2 </math> med <math> \,x_1 + h </math> och <math> \, x_2 - x_1 </math> med <math> \, h </math>. Då kan vi definiera:
+
−
 
+
−
 
+
−
<div class="border-divblue">
+
−
<b><span style="color:#931136">Funktionen <small><math> \, y = f\,(x)</math></small>:s genomsnittliga förändringshastighet i ett intervall av längden <small><math> \, h \, </math></small>:</span></b>
+
−
 
+
−
 
+
−
:::<small><math> \quad \displaystyle {{\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h}} \qquad {\rm i\;\;intervallet } \qquad x_1 \,\leq\, x \,\leq\, x_1 + h </math></small>
+
−
</div>
+
−
 
+
−
 
+
−
Observera att en funktions genomsnittliga förändringshastighet endast kan definieras i ett givet intervall på <math> \, x</math>-axeln.
+
  
  
 +
<small>
 
<div class="exempel">
 
<div class="exempel">
−
==== <b><span style="color:#931136">Beteckningar</span></b> ====
+
==== <b><span style="color:#931136">Exempel 3 Oljetank</span></b> ====
−
 
+
−
Kärt barn har många namn: &nbsp; Uttrycken i definitionen ovan har ett antal beteckningar som allihopa är synonymer:
+
−
 
+
−
::::::::<strong><span style="color:red">Genomsnittlig förändringshastighet</span></strong>
+
−
 
+
−
::::::::<strong><span style="color:red">Förändringskvot</span></strong>
+
−
 
+
−
::::::::<strong><span style="color:red">Ändringskvot</span></strong>
+
−
 
+
−
::::::::<strong><span style="color:red">Differenskvot</span></strong>
+
−
</div>
+
−
 
+
−
 
+
−
<div class="exempel">
+
−
=== <b><span style="color:#931136">Exempel 3 Oljetank</span></b> ===
+
 
<table>
 
<table>
 
<tr>
 
<tr>
Rad 154: Rad 119:
 
&nbsp; &nbsp; &nbsp; &nbsp;från början tills tanken är tom.
 
&nbsp; &nbsp; &nbsp; &nbsp;från början tills tanken är tom.
  
−
'''c)''' &nbsp;&nbsp; Beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet <math> 20 \leq x \leq 30 </math>.
+
'''c)''' &nbsp;&nbsp; Beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet <math> \, 20 \leq x \leq 30 \, </math>.
  
 
'''d)''' &nbsp;&nbsp; När är oljans utströmningshastighet störst? Beräkna ett närmevärde till denna hastighet.
 
'''d)''' &nbsp;&nbsp; När är oljans utströmningshastighet störst? Beräkna ett närmevärde till denna hastighet.
Rad 161: Rad 126:
 
</tr>
 
</tr>
 
</table>
 
</table>
−
</div> <!-- exempel3 -->
+
'''Lösning:'''
  
 +
'''a)'''&nbsp;&nbsp;Se grafen ovan.
  
−
'''Lösning:'''
+
'''b)'''&nbsp;&nbsp;Grafen tyder på att tanken kommer att vara tom efter ca. <math> \, 45 \, </math> minuter.
  
−
'''a)''' &nbsp;&nbsp; Se grafen ovan.
+
:Den exakta tiden får man genom att sätta volymen <math> \, y \, </math> till <math> \, 0 \, </math> dvs genom att lösa 2:a gradsekvationen<span style="color:black">:</span>
  
−
'''b)''' &nbsp;&nbsp; Grafen tyder på att tanken kommer att vara tom efter ca. <math> \, 45 \, </math> minuter. Den exakta tiden får man genom att sätta volymen <math> \, y \, </math> till <math> \, 0 \, </math> dvs genom att lösa 2:a gradsekvationen:
+
<math> \qquad 4\,x^2 - 380\,x + 9\,000 = 0 \qquad </math> [[1.1_Fördjupning_till_Polynom#Digital_ber.C3.A4kning_av_nollst.C3.A4llen|<b><span style="color:blue">Räknarens ekvationslösare</span></b>]] visar att <math> \, x = 45\, </math> är även den exakta lösningen.
  
−
:::<math> 4\,x^2 - 380\,x + 9\,000 = 0 </math>
+
:Därför är hela tidsintervallet från början tills tanken är tom<span style="color:black">:</span> <math> \, 0 \leq x \leq 45 \, </math>.
  
−
[[1.1_Fördjupning_till_Polynom#Digital_ber.C3.A4kning_av_nollst.C3.A4llen|<strong><span style="color:blue">Räknarens ekvationslösare</span></strong>]] visar att <math> x = 45\, </math> är den exakta tiden. Därför är hela tidsintervallet från början tills tanken är tom <math> 0 \leq x \leq 45 </math>. I detta intervall är oljans genomsnittliga utströmningshastighet:
+
:I detta intervall är oljans genomsnittliga utströmningshastighet<span style="color:black">:</span>
  
 
:::<math> {\Delta y \over \Delta x} = {f(45) \, - \, f(0) \over 45 - 0} = {0 \, - \, 9000 \over 45} = {-9000 \over 45} = -200 </math>
 
:::<math> {\Delta y \over \Delta x} = {f(45) \, - \, f(0) \over 45 - 0} = {0 \, - \, 9000 \over 45} = {-9000 \over 45} = -200 </math>
  
−
I hela tidsintervallet <math> 0 \leq x \leq 45 </math> sjunker oljans volym med <math> \, 200 \, </math> liter per minut.
+
:Dvs i intervallet <math> \, 0 \leq x \leq 45 \, </math> sjunker oljans volym med <math> \, 200 \, </math> liter per minut.
  
  
−
'''c)''' &nbsp;&nbsp; Oljans genomsnittliga utströmningshastighet i tidsintervallet <math> 20 \leq x \leq 30 </math>:
+
'''c)'''&nbsp;&nbsp;Oljans genomsnittliga utströmningshastighet i intervallet <math> \, 20 \leq x \leq 30 \, </math><span style="color:black">:</span>
  
 
:::<math> f\,(30) = 4 \cdot 30^2 - 380 \cdot 30 + 9\,000 = 1200 </math>
 
:::<math> f\,(30) = 4 \cdot 30^2 - 380 \cdot 30 + 9\,000 = 1200 </math>
Rad 187: Rad 153:
 
:::<math> {\Delta y \over \Delta x} = {f(30) \, - \, f(20) \over 30 - 20} = {1200 \, - \, 3000 \over 30 - 20} = {-1800 \over 10} = -180 </math>
 
:::<math> {\Delta y \over \Delta x} = {f(30) \, - \, f(20) \over 30 - 20} = {1200 \, - \, 3000 \over 30 - 20} = {-1800 \over 10} = -180 </math>
  
−
I tidsintervallet <math> 20 \leq x \leq 30 </math> sjunker oljans volym med <math> \, 180 \, </math> liter per minut.
+
:Dvs i intervallet <math> \, 20 \leq x \leq 30 \, </math> sjunker oljans volym med <math> \, 180 \, </math> liter per minut.
  
  
−
'''d)''' &nbsp;&nbsp; Grafen i '''a)''' visar att kurvans lutning är störst i början dvs vid tiden <math> x = 0\, </math> när oljan har mest volym, nämligen <math> 9\,000 </math> liter. Därför är även oljans utströmningshastighet störst vid denna tidpunkt. Men denna hastighet är inte längre genomsnittlig i något intervall utan ögonblicklig vid en viss tidpunkt eller <strong><span style="color:red">momentan</span></strong>.
+
'''d)'''&nbsp;&nbsp;Grafen i '''a)''' visar att kurvans lutning är störst i början dvs vid tiden <math> x = 0\, </math> när oljan har mest volym, nämligen <math> 9\,000 </math> liter.
  
−
För att beräkna den momentana och därmed den exakta utströmningshastigheten vid tiden <math> x = 0\, </math> måste man bestämma funktionen <math> y\, </math>:s exakta derivata, vilket vi inte lärt oss ännu.  
+
:Därför är även oljans utströmningshastighet störst vid denna tidpunkt.
  
−
För att approximera den momentana utströmningshastigheten vid tiden <math> x = 0\, </math> så noggrant som möjligt måste vi välja ett så litet tidsintervall som möjligt med <math> x = 0\, </math> som undre intervallgräns.
+
:Men denna hastighet är inte längre genomsnittlig i något intervall utan ögonblicklig vid en viss tidpunkt eller <b><span style="color:red">momentan</span></b>.
  
−
Låt oss t.ex. beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet <math> 0 \leq x \leq 0,1 </math>:
+
:För att beräkna den momentana (exakta) utströmningshastigheten vid tiden <math> \, x = 0\, </math> måste man bestämma funktionen <math> \, y\, </math>:s derivata.
 +
 
 +
:För att närma oss den exakta hastigheten vid tiden <math> \, x = 0\, </math> väljer vi ett så litet tidsintervall som möjligt med <math> \, x = 0\, </math> som undre intervallgräns.
 +
 
 +
:Låt oss t.ex. välja intervallet <math> \, 0 \leq x \leq 0,1 \, </math><span style="color:black">:</span>
  
 
:::<math> f\,(0,1) = 4 \cdot 0,1^2 - 380 \cdot 0,1 + 9\,000 = 8962,04 </math>
 
:::<math> f\,(0,1) = 4 \cdot 0,1^2 - 380 \cdot 0,1 + 9\,000 = 8962,04 </math>
Rad 202: Rad 172:
 
:::<math> {\Delta y \over \Delta x} = {f(0,1) \, - \, f(0) \over 0,1 - 0} = {8962,04 \, - \, 9000 \over 0,1} = {-37,96 \over 0,1} = -379,6 </math>
 
:::<math> {\Delta y \over \Delta x} = {f(0,1) \, - \, f(0) \over 0,1 - 0} = {8962,04 \, - \, 9000 \over 0,1} = {-37,96 \over 0,1} = -379,6 </math>
  
−
I tidsintervallet <math> 0 \leq x \leq 0,1 </math> sjunker oljans volym med <math> 379,6\, </math> liter per minut.
+
:I intervallet <math> \, 0 \leq x \leq 0,1 \, </math> sjunker oljans volym med <math> 379,6\, </math> liter per minut.
 +
 
 +
:Faktiskt är denna approximation inget dåligt närmevärde, för den momentana utströmningshastigheten vid tiden <math> x = 0\, </math> (exakta värdet) är <math> -380\, </math>.
 +
 
 +
:I avsnittet [[2.4 Derivatans definition|<b><span style="color:blue">2.4 Derivatans definition</span></b>]] kommer vi att lära oss hur man får reda på det exakta värdet.
 +
</div> <!-- exempel3 -->
 +
</small>
 +
 
 +
 
 +
</div> <!-- "ovnC" -->
 +
 
 +
 
 +
=== <b><span style="color:#931136">Allmän definition</span></b> ===
 +
'''Givet''': &nbsp; &nbsp; &nbsp; &nbsp;Funktionen <math> y \, = \, f\,(x) </math> i form av en formel, tabell eller graf.
 +
 
 +
:::Något intervall på <math> x\, </math>-axeln med givna gränser <math> \, x_1 \, </math> och <math> \, x_2 \, </math> dvs <math> \; x_1 \,\leq\, x \,\leq\, x_2 </math>.
 +
 
 +
'''Sökt''': &nbsp; &nbsp; &nbsp; &nbsp; Funktionens genomsnittliga förändringshastighet i intervallet <math> \, x_1 \,\leq\, x \,\leq\, x_2 </math>.
 +
 
 +
'''Lösning''': &nbsp; &nbsp; <math> \displaystyle{{\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} \; = \; {y_2 - y_1 \over x_2 - x_1} \; = \; {\boxed {f(x_2) \, - \, f(x_1) \over x_2 - x_1}}} \quad {\rm Detta\;uttryck\;har\;använts\;i\;exemplen\;ovan.} </math>
 +
 
 +
En annan form får vi om vi inför en ny beteckning <math> \, h\, </math> för intervallets längd:
 +
 
 +
::::<math>\begin{align} h & = x_2 - x_1  \qquad  & | \; + \, x_1 \\
 +
                  x_1 + h & = x_2                                \\
 +
          \end{align}</math>
 +
 
 +
Om vi nu i det inramade uttrycket ovan ersätter <math> \, x_2 </math> med <math> \,x_1 + h </math> och <math> \, x_2 - x_1 </math> med <math> \, h </math>, får vi den allmänna definitionen:
 +
 
 +
<div class="border-divblue">
 +
<b><span style="color:#931136">Funktionen <small><math> \, y = f\,(x)</math></small>:s &nbsp; <span style="color:red">genomsnittliga förändringshastighet</span> &nbsp; i ett intervall av längden <math> \, h \, </math> är:</span></b>
 +
 
 +
::::<small><math> \quad \displaystyle {{\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h}} \qquad {\rm i\;\;intervallet } \qquad x_1 \,\leq\, x \,\leq\, x_1 + h </math></small>
 +
</div>
 +
 
 +
Observera att den genomsnittliga förändringshastigheten endast kan definieras i ett givet <b><span style="color:red">intervall</span></b> på <math> \, x</math>-axeln.
 +
 
 +
 
 +
<div class="exempel">
 +
==== <b><span style="color:#931136">Beteckningar</span></b> ====
 +
 
 +
Uttrycket <math> \quad \displaystyle {{\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h}} \quad </math> kommer att användas i fortsättningen i detta kapitel och har ett antal beteckningar
 +
 
 +
som allihopa är synonymer:
 +
 
 +
::::::<b><span style="color:red">Genomsnittlig förändringshastighet</span></b>
 +
 
 +
::::::<b><span style="color:red">Förändringskvot</span></b>
 +
 
 +
::::::<b><span style="color:red">Ändringskvot</span></b>
 +
 
 +
::::::<b><span style="color:red">Differenskvot</span></b>
 +
 
 +
Kärt barn har många namn.
 +
</div>
 +
 
 +
 
  
−
Faktiskt är denna approximation inget dåligt närmevärde för den momentana utströmningshastigheten vid tiden <math> x = 0\, </math>, för det exakta värdet är <math> -380\, </math>. I avsnittet [[Detta avsnitt ingår inte i demon.|<strong><span style="color:blue">2.4 Derivatans definition</span></strong>]] kommer vi att lära oss hur man får reda på det exakta värdet.
 
  
  
−
== <b><span style="color:#931136">Internetlänkar</span></b> ==
+
=== <b><span style="color:#931136">Internetlänkar</span></b> ===
 
http://www.youtube.com/watch?v=08yI3grz17I
 
http://www.youtube.com/watch?v=08yI3grz17I
  

Versionen från 9 oktober 2016 kl. 18.43

       \( \pmb{\gets} \) Förra avsnitt          Genomgång          Övningar          Nästa demoavsnitt \( \pmb{\to} \)      


Lektion 13: Genomsnittlig förändringshastighet

Tre exempel på genomsnittlig förändringshastighet


Exempel 1 Marginalskatt

Martins månadslön höjs från \( \, 23\;000 \, \) kr till \( \, 24\;200 \, \) kr.

I Skatteverkets skattetabell för 2015 (tabell 29, kolumn 2) hittar vi

\( \, 5\;297 \, \) kr skatt för den gamla och \( \, 5\;676 \, \) kr skatt för den nya lönen.

Beräkna marginalskatten som är skattens procentuella andel i varje mer intjänad krona.

Matematiskt är marginalskatten skattens genomsnittliga förändringshastighet när skatten uppfattas som en funktion av lönen.

Lösning:

Skatten \( \, y \, \) kan definieras som en diskret funktion av lönen \( \, x\, \) i tabellform:

\( x\, \) \( y\, \)
\( 23\,000 \) \( 5\,297\)
\( 24\,200 \) \( 5\,676 \)
\( \qquad\qquad \) \( x \, = \, {\rm Månadslönen\;i\;kr} \)

\( y \, = \, {\rm Skatten\;i\;kr} \)

Förhållandet (kvoten) mellan skattehöjning och lönehöjning kallas för funktionen \( \, y\):s genomsnittliga förändringshastighet:

\[ {\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} = {{\rm Skattehöjningen} \over {\rm Lönehöjningen}} = {5\,676 - 5\,297 \over 24\,200 - 23\,000} \; = \; {379 \over 1200} \; = \; {\color{Red} {0,316}} \; = \; 31,6 \, \%\]

I intervallet \( \; 23\,000 \,\leq\, x \,\leq\, 24\,200 \, \) har funktionen \( \, y \, \) den genomsnittliga förändringshastigheten \( \; {\color{Red} {0,316}} \).

Dvs \( \, y \, \) växer i detta intervall med \( {\color{Red} {0,316}} \; y\)-enheter per \( x\)-enhet.

Ekonomisk tolkning:   Martin måste betala \( \, 31,6\,\) öre i skatt för varje mer intjänad krona. Man säger: marginalskatten är \( \, 31,6 \, \% \).


Vi ersätter nu den diskreta skattefunktionen i tabellform med en kontinuerlig funktion som är given med ett algebraiskt uttryck:


Exempel 2 Kvadratisk funktion

Givet:        Funktionen \( \, y \, = \, f(x) \, = \, x^2 \)
Intervallet \( \, 0 \,\leq\, x \,\leq\, 2 \)

Sökt:         Funktionens genomsnittliga förändringshastighet i intervallet \( \, 0 \leq x \leq 2 \).

Lösning:

\[ {\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} \; = \; {f(2) \, - \, f(0) \over 2 - 0} \; = \; {2^2 \, - \, 0^2 \over 2 - 0} \; = \; {4 \, - \, 0 \over 2} \; = \; {4 \over 2} \; = \; {\color{Red} 2} \]

I intervallet \( \, 0 \leq x \leq 2 \, \) har funktionen \( \, y = x^2 \, \) den genomsnittliga förändringshastigheten \( \, {\color{Red} 2} \).

Dvs funktionen \( \, y = x^2 \, \) växer i detta intervall med \( \, {\color{Red} 2} \; y\)-enheter per \( \, x\)-enhet.

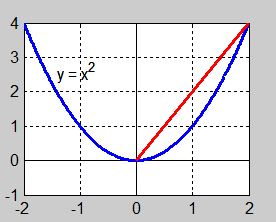
        Ex1a.jpg

Geometrisk tolkning:    Om man ersätter kurvan \( \, y = x^2 \, \) med en rät linje har denna linje som kallas för kurvans sekant, lutningen \( \, {\color{Red} 2} \).

Sekantens lutning är kurvans genomsnittliga förändringshastighet i intervallet \( \, 0 \leq x \leq 2 \).




Exempel 3 Oljetank

En oljetank läcker genom ett hål i tankens botten.

Utströmningen av oljan beskrivs av funktionen:

\[ y \, = \, 4\,x^2 - 380\,x + 9\,000 \]

där \( \; \quad \! x \, = \, {\rm Tiden\;i\;minuter} \)

\[ y \, = \, {\rm Oljans\;volym\;i\;liter} \]

a)    Rita grafen till funktionen som beskriver utströmningen.

b)    Hur stor är oljans genomsnittliga utströmningshastighet i hela tidsintervallet

       från början tills tanken är tom.

c)    Beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet \( \, 20 \leq x \leq 30 \, \).

d)    När är oljans utströmningshastighet störst? Beräkna ett närmevärde till denna hastighet.

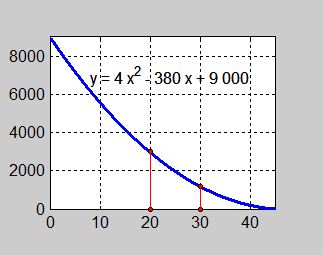
        Ex2a.jpg

Lösning:

a)  Se grafen ovan.

b)  Grafen tyder på att tanken kommer att vara tom efter ca. \( \, 45 \, \) minuter.

Den exakta tiden får man genom att sätta volymen \( \, y \, \) till \( \, 0 \, \) dvs genom att lösa 2:a gradsekvationen:

\( \qquad 4\,x^2 - 380\,x + 9\,000 = 0 \qquad \) Räknarens ekvationslösare visar att \( \, x = 45\, \) är även den exakta lösningen.

Därför är hela tidsintervallet från början tills tanken är tom: \( \, 0 \leq x \leq 45 \, \).
I detta intervall är oljans genomsnittliga utströmningshastighet:
\[ {\Delta y \over \Delta x} = {f(45) \, - \, f(0) \over 45 - 0} = {0 \, - \, 9000 \over 45} = {-9000 \over 45} = -200 \]
Dvs i intervallet \( \, 0 \leq x \leq 45 \, \) sjunker oljans volym med \( \, 200 \, \) liter per minut.


c)  Oljans genomsnittliga utströmningshastighet i intervallet \( \, 20 \leq x \leq 30 \, \):

\[ f\,(30) = 4 \cdot 30^2 - 380 \cdot 30 + 9\,000 = 1200 \]
\[ f\,(20) = 4 \cdot 20^2 - 380 \cdot 20 + 9\,000 = 3000 \]
\[ {\Delta y \over \Delta x} = {f(30) \, - \, f(20) \over 30 - 20} = {1200 \, - \, 3000 \over 30 - 20} = {-1800 \over 10} = -180 \]
Dvs i intervallet \( \, 20 \leq x \leq 30 \, \) sjunker oljans volym med \( \, 180 \, \) liter per minut.


d)  Grafen i a) visar att kurvans lutning är störst i början dvs vid tiden \( x = 0\, \) när oljan har mest volym, nämligen \( 9\,000 \) liter.

Därför är även oljans utströmningshastighet störst vid denna tidpunkt.
Men denna hastighet är inte längre genomsnittlig i något intervall utan ögonblicklig vid en viss tidpunkt eller momentan.
För att beräkna den momentana (exakta) utströmningshastigheten vid tiden \( \, x = 0\, \) måste man bestämma funktionen \( \, y\, \):s derivata.
För att närma oss den exakta hastigheten vid tiden \( \, x = 0\, \) väljer vi ett så litet tidsintervall som möjligt med \( \, x = 0\, \) som undre intervallgräns.
Låt oss t.ex. välja intervallet \( \, 0 \leq x \leq 0,1 \, \):
\[ f\,(0,1) = 4 \cdot 0,1^2 - 380 \cdot 0,1 + 9\,000 = 8962,04 \]
\[ {\Delta y \over \Delta x} = {f(0,1) \, - \, f(0) \over 0,1 - 0} = {8962,04 \, - \, 9000 \over 0,1} = {-37,96 \over 0,1} = -379,6 \]
I intervallet \( \, 0 \leq x \leq 0,1 \, \) sjunker oljans volym med \( 379,6\, \) liter per minut.
Faktiskt är denna approximation inget dåligt närmevärde, för den momentana utströmningshastigheten vid tiden \( x = 0\, \) (exakta värdet) är \( -380\, \).
I avsnittet 2.4 Derivatans definition kommer vi att lära oss hur man får reda på det exakta värdet.



Allmän definition

Givet:        Funktionen \( y \, = \, f\,(x) \) i form av en formel, tabell eller graf.

Något intervall på \( x\, \)-axeln med givna gränser \( \, x_1 \, \) och \( \, x_2 \, \) dvs \( \; x_1 \,\leq\, x \,\leq\, x_2 \).

Sökt:         Funktionens genomsnittliga förändringshastighet i intervallet \( \, x_1 \,\leq\, x \,\leq\, x_2 \).

Lösning:     \( \displaystyle{{\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} \; = \; {y_2 - y_1 \over x_2 - x_1} \; = \; {\boxed {f(x_2) \, - \, f(x_1) \over x_2 - x_1}}} \quad {\rm Detta\;uttryck\;har\;använts\;i\;exemplen\;ovan.} \)

En annan form får vi om vi inför en ny beteckning \( \, h\, \) för intervallets längd:

\[\begin{align} h & = x_2 - x_1 \qquad & | \; + \, x_1 \\ x_1 + h & = x_2 \\ \end{align}\]

Om vi nu i det inramade uttrycket ovan ersätter \( \, x_2 \) med \( \,x_1 + h \) och \( \, x_2 - x_1 \) med \( \, h \), får vi den allmänna definitionen:

Funktionen \( \, y = f\,(x)\):s   genomsnittliga förändringshastighet   i ett intervall av längden \( \, h \, \) är:

\( \quad \displaystyle {{\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h}} \qquad {\rm i\;\;intervallet } \qquad x_1 \,\leq\, x \,\leq\, x_1 + h \)

Observera att den genomsnittliga förändringshastigheten endast kan definieras i ett givet intervall på \( \, x\)-axeln.


Beteckningar

Uttrycket \( \quad \displaystyle {{\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h}} \quad \) kommer att användas i fortsättningen i detta kapitel och har ett antal beteckningar

som allihopa är synonymer:

Genomsnittlig förändringshastighet
Förändringskvot
Ändringskvot
Differenskvot

Kärt barn har många namn.



Internetlänkar

http://www.youtube.com/watch?v=08yI3grz17I

http://www.youtube.com/watch?v=Cze2KrRhHiM

http://www.iceclimbers.net/fil/matematik_c/12.genomsnittlig_forandringshastighet.pdf

http://ingforum.haninge.kth.se/matCD/F%F6rel%E4sning01.pdf




Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.

Hämtad från "https://minidemo.mathonline.se/index.php?title=2.2_Genomsnittlig_förändringshastighet&oldid=27050"