3.3 Lösning 6b
Från Mathonline
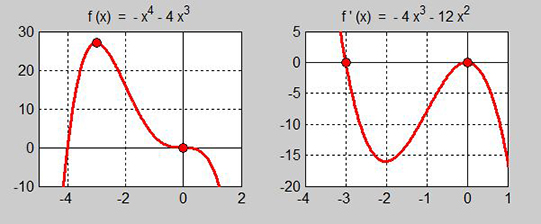
Funktionens graf till vänster visar:
\( f(x) \;\; {\rm har\;en\;terasspunkt\;i} \;\; x = 0 \;\; {\rm och\;en\;maximipunkt\;i} \;\; x = -3 \).
Derivatans graf till höger visar att \( f'(x) \;\; {\rm har\;nollställen\;i} \;\; x = 0 \;\; {\rm och\;i} \;\; x = -3 \).
Derivatans nollställe i \( \, x = 0 \, \) är en dubbelrot (byter inte tecken) vilket innebär att funktionen har en terasspunkt i \( \, x = 0 \, \).
Derivatans nollställe i \( \, x = -3 \, \) är av enkel typ vilket medför att funktionen har en extrempunkt i \( \, x = -3 \, \).
Derivatan byter tecken kring nollstället \( \, x = -3 \, \) från \( \, + \, \) till \( \, - \, \) vilket visar att funktionens extrempunkt i \( \, x = -3 \, \) är en maximipunkt.