3.3 Ekvationer

Genomgång

Quiz

Övningar

Genomgång+

Nästa demoavsnitt  >>

Varför ekvationer? Exempel på en textuppgift: Kalle köper en flaska dryck som kostar $\, 18 \,$ kr med pant. Drycken (innehållet) kostar $\, 14 \,$ kr mer än panten (flaskan). Hur mycket kostar flaskan? Utan ekvation svarar de flesta 4 kr, vilket är fel. Lösning med ekvation: $\quad\;\;\; x \; = \; {\rm flaskans\;pris}$ $$\qquad\qquad\;\; x \, + \, 14 \; = \; {\rm dryckens\;pris}$$ $$\begin{array}{rcl} x \, + \, (x \, + \, 14) & = & 18 \\ x \, + \, x \, + \, 14 & = & 18 \\ 2\,x \, + \, 14 & = & 18 \\ 2\,x \, & = & 4 \\ x \, & = & {\color{Red} 2} \end{array}$$ Svar:     Flaskan kostar $\, {\color{Red} {2 \; {\rm kr\,}}}$. För mer info om hur man ställer upp en ekvation och om lösningsmetoder se: Metoden att ställa upp en ekvation utifrån en textuppgift, Övertäckningsmetoden $\quad$ och $\quad$ Allmän metod.

$\;\;$

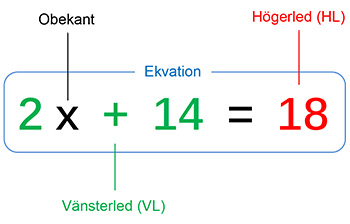
Vad är en ekvation? $\qquad\quad$ En ekvation är en likhet mellan två uttryck, har alltid formen VL = HL och innehåller minst en variabel, kallad obekant. Ex.: $\qquad\quad 2\,x \; + \; 14 \; = \; 18$ Ekvationens lösning: $\quad\;$ $x \; = \; {\color{Red} 2}$ Varför lösning? Kontroll: Sätt in lösningen i ekvationen. VL $\, = \, 2 \, \cdot \, {\color{Red} 2} \, + \, 14 \, = \, 4 \, + \, 14 \, = \, 18$ HL $\, = \, 18$ VL $=$ HL $\, \implies \, x = {\color{Red} 2}$ är en lösning. Kontroll kallas ibland även för prövning.

Om kontrollen ovan säger man: Lösningen satisfierar (uppfyller) ekvationen.

Men hur får man lösningen? Det finns två lösningsmetoder:

1.   Övertäckningsmetoden

Exemplet ovan:

  $2 \, x \;\; + \; 14 \; = \; 18 \quad {\color{Red} {\rm Täck\;över\;}} 2 \, x$

$\quad$

$\, + \;\, 14 \; = \; 18$

  $\;\, {\color{Red} ?} \;\;\; + \; 14 \; = \; 18$

  $\;\, {\color{Red} 4} \;\;\; + \; 14 \; = \; 18$

  $\;\, \Downarrow$

  $\, 2 \, \cdot \; x \;\; = \;\, {\color{Red} 4} \qquad\quad {\color{Red} {\rm Täck\;över\;}} x$

  $\, 2 \, \cdot \;$

$\quad$

$\; = \;\, 4$

  $\, 2 \, \cdot \; {\color{Red} ?} \;\; = \;\; 4$

  $\, 2 \, \cdot \; {\color{Red} 2} \;\; = \;\; 4$

  $\quad\;\;\; \Downarrow$

 

$\; x \; = \; {\color{Red} 2}$

2.   Allmän metod

Exempel:

$$\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & \qquad | & {\color{Red} {- \, 14}} \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} & & \\ 2 \cdot x \, & = & 4 & \qquad | & {\color{Red} {/ \; 2}} \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x \, & = & 2 & & \end{array}$$

Skrivsättet $\quad\;\;\, | \quad {\color{Red} {- \, 14}} \quad\;\;\,$ är en kommentar och betyder:

Subtrahera $\, 14 \,$ från ekvationens båda led.

Kommentaren $\;\; | \quad {\color{Red} {/ \; 2}} \;\;$ betyder:

Dividera ekvationens båda led med $\, 2$.

Den allmänna metoden steg för steg

Steg 1

  Förenkla uttrycken i ekvationens båda led

  så långt som möjligt. I exemplet ovan:

$$\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & & \end{array}$$

Steg 2

  Utför samma operation på båda leden:

$$\begin{array}{rcl} 2\,x \, + \, 14 & = & 18 \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} \\ 2\,x \, & = & 4 \end{array}$$

Vilken operation?

Den inversa operation som isolerar $x$-termen.

$\;\;\; {\color{Red} {- \, 14}} \,$ är den inversa operationen till $\, + \, 14$

Steg 3

  Utför samma operation på båda leden:

$$\begin{array}{rclcl} \quad\; 2 \cdot x \, & = & 4 & & \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x & = & 2 & & \end{array}$$

Vilken operation?

Den inversa operation som isolerar $\, x \,$.

$\quad\;\; {\color{Red} {/ \; 2}} \,$ är den inversa operationen till $\, \cdot \; 2$

Den allmänna metodens filosofi:

Betrakta ekvationen som en våg i balans.

HL och VL är vågens skålar. Likhetsteck-

net betyder att vågens skålar är i balans.

Bibehåll balansen genom att utföra:

$\;\;\;$ Samma operation på båda leden !

Välj alltid den inversa operationen till den

operation som binder $\, x \,$ till dess omgivning.

När saknar en ekvation lösning?

Exempel:

$\begin{array}{rcl} 2\,x \, - \, 2\, (3 \, + \, x ) & = & 8 \\ 2\,x \, - \, 6 \, - \, 2\,x & = & 8 \\ - \, 6 & = & 8 \quad {\color{Red} {\rm{Motsägelse!}}} \\ & \Downarrow & \end{array}$

$\qquad\quad$ Ekvationen saknar lösning.

När är alla tal lösningar till en ekvation?

Exempel:

$\begin{array}{rcl} \;\; x \, - \, (4 \, + \, x ) & = & -4 \\ x \, - \, 4 \, - \, x & = & -4 \\ - \, 4 & = & -4 \quad {\color{Red} {\rm{Alltid\;sant!}}} \\ & \Downarrow & \end{array}$

$\;\;$ Alla tal är lösningar till ekvationen. Eller:

$\;\;$ Ekvationen har oändligt många lösningar.

Copyright © 2021 TechPages AB. All Rights Reserved.