2.6 Derivatan av exponentialfunktioner

<<  Förra demoavsnitt

Genomgång

Övningar

Nästa demoavsnitt  >>

Målet i detta avsnitt är att ställa upp deriveringsregeln för den allmänna exponentialfunktionen $\, y = a\,^x \,$ med en godtycklig bas $a > 0$.

Detta gör vi genom att först härleda derivatan av exponentialfunktionen $\, y = e\,^x \,$ med basen $\, e =$ Eulers tal

och sedan gå över till godtycklig bas $\,a$. Rpeptera gärna Talet e och den naturliga logaritmen från kap 1 Algebra & funktioner.

Deriveringsregeln för $y \, = \, e\,^x$

Derivatan av exponentialfunktionen med basen $\, e \,$ är funktionen själv:

$$\begin{array}{llcl} {\rm Om} & y & = & e\,^x \;\; {\rm där} \;\; e = {\rm Eulers\;tal} \\ {\rm då} & y\,' & = & e\,^x \end{array}$$

OBS!    Förväxla denna regel inte med Regeln om derivatan av en potens, därför att:

$y \, = \, e\,^x \,$ är ingen potens- utan en exponentialfunktion. $\, x \,$ förekommer i exponenten, inte i basen.

Ex.: Derivatan av $\, f(x) = e\,^2 \,$ är inte $\, 2 \, e \,$ utan $\; f\,'(x) = 0 \;$, för $\, e \, \, = \, 2,718281828\ldots$ är en konstant och därmed även $\, e\,^2 \,$.

Ett försök med derivatans definition

Derivatans definition för $\, y = f(x) = e\,^x \,$ leder till:

$$y\,' = \lim_{h \to 0}\,{f(x + h) - f(x) \over h} = \lim_{h \to 0}\,{e\,^{x + h} - e\,^x \over h} = \lim_{h \to 0}\,{e\,^x \cdot e\,^h - e\,^x \over h} = \lim_{h \to 0}\,{e\,^x \, (e\,^h - 1) \over h} = e\,^x \cdot \lim_{h \to 0}\,{e\,^h - 1 \over h}$$

Det är lite svårt för oss att inse att värdet på den sista limes är $\, 1$. Detta kan t.ex. visas med den s.k. potensserieutvecklingen av $\, e\,^x$ $-$ som dock inte ingår i gymnasiematematiken. Så vi kan inte slutföra beviset med derivatans definition.

Därför väljer vi en annan metod för att bevisa deriveringsregeln $\; y = e\,^x \, \Rightarrow \, y\,' = e\,^x \,$.

Ny bevisidé

Kan bland exponentialfunktionerna $\; y = b\,^x \;$ basen $\, b \,$ väljas så att derivatan blir samma som funktionen: $\; y\,' = b\,^x$   ?

Istället för att fråga efter derivatan, kräver vi derivatan = funktionen och frågar efter en bas som uppfyller detta krav.

Svaret ges av Eulers bevis nedan.

Frågeställningen ovan har i matematikens historia motiverat den schweiziske matematikern Leonard Euler att ställa upp sin berömda formel för beräkning av talet $\, e \,$ som redan nämndes i Hur kom(mer) talet $\, e \,$ till? och som vi nu med limes kan formulera så här:

$$\lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \; =\; e \; = \; 2,718281828\ldots$$

På 1700-talet bevisade Euler denna formel, varför talet $\, e \,$ kallats efter honom.

Eulers bevis

Vi antar att det finns en bas $\,b \, > \, 0$ $-$ som än så länge är okänd $-$ så att:

$$\begin{array}{lclcl} y & = & f\,(x) & = & b\,^x \\ {\color{Red} {y\,'}} & {\color{Red} =} & {\color{Red} {f\,'\,(x)}} & {\color{Red} =} & {\color{Red} {b\,^x}} \end{array}$$

I den andra raden har vi formulerat kravet: derivatan = funktionen.

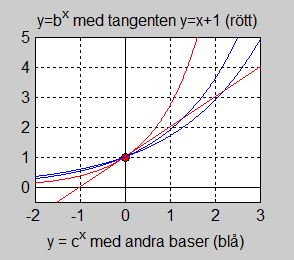
Nu konstruerar vi tangenten till $y = b\,^x$ i punkten $\,x = 0$:

Ekvationen för tangenten till kurvan $y = b\,^x$ i punkten $\,x = 0$ har $\,k$-formen $\; y \, = \, k\,x \, + \, m \;$ .

Från tidigare vet vi att tangenten till kurvan $\, y = b\,^x \,$ i $\, x = 0 \,$ har en lutning $\,k\,$ som är funktionens derivata i denna punkt.

Derivatan har vi: $\, {\color{Red} {f\,'(x) = b\,^x}} \,$ (se ovan). Så vi kan beräkna denna lutning: $$k \, = \, {\color{Red} {f\,'(0) \, = \, b\,^0}}\, = \, 1$$ Tangentens ekvation blir då $\, y \, = \, x \, + \, m \,$ i vilken vi sätter in tangeringspunktens koordinater $\, (0, \, b\,^0) \, = \, (0, 1) \,$ för att bestämma $\, m \,$: $$\begin{array}{rcl} y & = & x \, + \, m \\ 1 & = & 0 \, + \, m \\ 1 & = & m \end{array}$$ Således blir tangentens ekvation    $\boxed{\;y \, = \, x \, + \, 1\;}$

$\quad$

Andra exponentialfunktioner $\, y = c\,^x \,$ med $\, c \neq b \,$ skär denna tangent i två punkter, medan $\, y = b\,^x \,$ med $\, y\,' = b\,^x \,$ tangerar den i punkten $\, (0, 1)$.

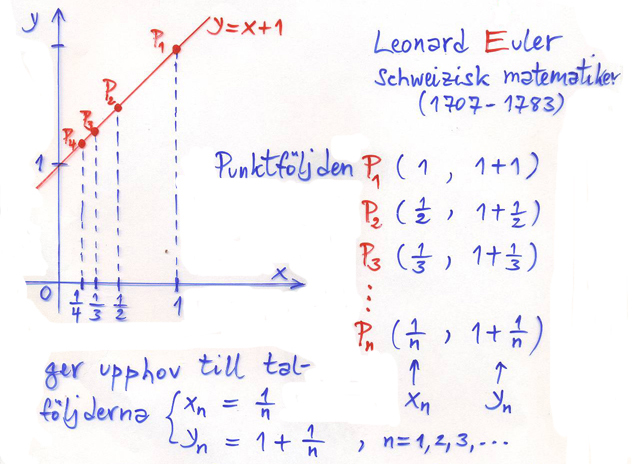
På tangenten $\, y = x + 1 \,$ konstruerar vi en punktföljd    $P_1, \, P_2, \, P_3, \, \ldots$    vars $\,x$-koordinater $\, x_n \,$ bildar talföljden:

$$1, \, {1 \over 2}, \, {1 \over 3}, \, {1 \over 4}, \, \ldots \quad {\rm med} \quad x_n \, = \, {1 \over n} \quad {\rm som\;allmän \;term,\;där:} \qquad n = 1,\,2,\,3,\,\ldots$$

Talföljden $\,x_n \,$ ger pga $\, y = x + 1 \,$ upphov till följande talföljd:

$\,y_n \, = \, x_n + 1 \, = \, {1 \over n} + 1 \, = \, 1 \, + \, {1 \over n} \,$ på $\,y$-axeln: $\qquad 1\!+\!1, \quad 1\!+\!{1 \over 2}, \quad 1\!+\!{1 \over 3}, \quad 1\!+\!{1 \over 4}, \, \ldots$ Punkterna $\, P_n = (x_n, \; y_n) = \left({1 \over n}, \; 1 + {1 \over n}\right) \,$ går mot   tangeringspunkten $\, (0, 1) \,$ när $\, n \to \infty$. Punktföljden $\, P_n \,$ ger upphov till en följd av exponen- tialfunktioner $\, y_n = b_n\,^{x_n} \,$ med vissa baser $\, b_n$, där: $\qquad\qquad b_n \to \, b \quad\; {\rm när} \quad\; n \to \infty$ och $\, b \,$ är den efterfrågade basen till $\, y = b\,^x \,$. Vi sätter in punktföljdernas allmänna termer $\, x_n = {1 \over n}$ och $\, y_n = 1 + {1 \over n} \,$ i funktionerna $\, y_n = b_n\,^{x_n}\,$: $$\begin{array}{rcll} y_n & = & b_n\,^{x_n} \\ \;\; 1 + {1 \over n} & = & b_n\,^{1 \over n} \qquad & | \quad (\,\cdot\,)\,^n \end{array}$$ $$\!\boxed{\;\left(1 + {1 \over n}\right)^n \, = \;\; b_n\;}$$ Nu tar vi $\, \displaystyle \lim_{n \to \infty} \,$ på båda leden för att få Eulers formel:

$\displaystyle \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \, = \, \lim_{n \to \infty} {b_n} \, = \, b \,$ som visar sig vara samma tal vars värde vi numeriskt hade fått fram i Hur kom(mer) talet $\, e \,$ till?  :

$n$	$1\,000$	$1000\,000$	$1000\,000\,000$	$10\,000\,000\,000$	$\to \infty$
$\left(1 + {1 \over n}\right)^n$	${\color{Red} {2,71}}6923932\ldots$	${\color{Red} {2,71828}}0469\ldots$	${\color{Red} {2,71828182}}7\ldots$	${\color{Red} {2,718281828\ldots}}$	$\quad \to \; {\color{Red} {{\rm Eulers\;tal\;} e}} \quad$

Detta demonstrerar att $\; \displaystyle \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \, = \, e \;$ dvs den efterfrågade basen $\, b \,$ är just Eulers tal $\, e \,$.

Den inledande frågan i Ny bevisidé kan nu besvaras:

Kan bland exponentialfunktionerna $\; y = b\,^x \;$ basen $\, b \,$ väljas så att derivatan blir samma som funktionen: $\; y\,' = b\,^x$   ?

Svar:

Ja, det är  basen $\, {\color{Red} {e = }}$ Eulers tal  som gör att derivatan av $\; y = e\,^x$ blir samma som funktionen: $\; {\color{Red} {y\,' = e\,^x}}$ .

Därför gäller Deriveringsregeln för $\, y \,= \,e\,^x \,$ som ställdes upp inledningsvis. Men:

Hur blir det när konstanter är inblandade?

Deriveringsregeln för $y = C\,e\,^{k\,x}$

Regel: $$\begin{array}{ll} {\rm Derivatan\;av} & y \;\, = \; C\;e\,^{k\,x} \;\; {\rm där} \;\; C,\,k = {\rm const.} \\ {\rm är} & y\,' = \; C\cdot k\cdot e\,^{k\,x} \end{array}$$ Om $\, C \,$, se Derivatan av en funktion med en konstant faktor. Om $\, k \,$, se Kedjeregeln i kursen Matematik 4.

$\quad$

Exempel 1 För funktionen $\;\, f(x) \; = \; 2\,e\,^{-\,x} \;$ blir derivatan: $$\;\, f\,'(x) \; = \; 2 \cdot (-1) \cdot e\,^{-\,x} \; = \; -2\,e\,^{-\,x}$$ Exempel 2 För funktionen   $f(x) \; = \; -4\,e\,^{-3\,x} \;$ blir derivatan: $$f\,'(x) \; = \; (-4) \cdot (-3) \cdot e\,^{-3\,x} \; = \; 12\,e\,^{-3\,x}$$

Från att ha ställt upp deriveringsregeln för $\, y = e\,^x \,$ går vi nu över till den allmänna exponentialfunktionen $\, y = a\,^x \,$ med godtycklig bas $a > 0\,$:

Deriveringsregeln för $\, y = a\,^x$

$$\begin{array}{llcl} {\rm Om} & y & = & a\,^x \;\; {\rm där} \;\; a = {\rm godtycklig\;konstant} \, > \,0 \\ {\rm då} & y\,' & = & a\,^x \, \cdot \, \ln a \end{array}$$

Specialfallet $\, a = e \,$ och $\ln a = \ln e = 1 \,$ ger derveringsregeln $\,y\,' = e^x \,$ för exponentialfunktionen med basen $\, e$.

Bevis

Vi börjar med att skriva om basen $\, a \,$ till $\,e\,^{\ln a} \,$, vilket är möjligt pga inversegenskapen. Då blir det:

$$\begin{array}{rcll} y & = & a\,^x \qquad & : \quad a \, = \,e\,^{\ln a} {\rm \;enligt\;inversegenskapen} \\ y & = & \left(e\,^{\ln a}\right)^x \qquad & : \quad {\rm 3:e\;potenslagen\;på\;HL} \\ y & = & e\,^{(\ln a) \, \cdot \, x} \qquad & : \quad \ln a \, = \, k \\ y & = & e\,^{k \, \cdot \, x} \qquad & | \quad {\rm Derivera\;enligt\;regeln\;ovan} \\ y\,' & = & k \, \cdot \, e\,^{k\,x} \qquad & : \quad k \, = \, \ln a \\ y\,' & = & (\ln a) \, \cdot \, e\,^{(\ln a)\,x} \qquad & : \quad {\rm 3:e\;potenslagen\;på\;HL} \\ y\,' & = & (\ln a) \, \cdot \, \left(e\,^{\ln a}\right)^x \qquad & : \quad e\,^{\ln a} \, = a\, {\rm \;enligt\;inversegenskapen} \\ y\,' & = & (\ln a) \, \cdot \, a^x \\ y\,' & = & a^x \, \cdot \, \ln a \end{array}$$

Ganska liknande basen $\, e \,$ blir det när konstanter är inblandade i den allmänna exponentialfunktionen $\, y = a\,^x \,$:

Deriveringsregeln för $y = C\,a\,^{k\,x}$

Derivatan av exponentialfunktionen $y = C\,a\,^{k\,x}$ med godtycklig bas $\, a > 0$ och $C,\,k = {\rm const.}$

$$\begin{array}{llcl} {\rm Om} & y & = & C\,a\,^{k\,x} \;\; {\rm där} \;\; a > 0,\;\; C,\,k = {\rm const.} \\ {\rm då} & y\,' & = & C\cdot k\cdot a\,^{k\,x} \cdot \ln a \end{array}$$

Uppdaterad tabell över deriveringsregler

Vi utvidgar tabellen över deriveringsregler från förra avsnitt med våra nya resultat i detta avsnitt.

I följande tabell är $C,\,c,\,a,\,k,\,m,\,n$ konstanter medan $x\,$ och $y\,$ är variabler:

$y\,$	$y\,'$
$c\,$	$0\,$
$x\,$	$1\,$
$a\; x$	$a\,$
$k\; x \, + \, m$	$k\,$
$x^2\,$	$2\,x$
$a\,x^2$	$2\,a\,x$
$x^n\,$	$n\cdot x\,^{n-1}$
$a\,x\,^n$	$a\cdot n\cdot x\,^{n-1}$
$\displaystyle {1 \over x}$	$\displaystyle - {1 \over x^2}$
$\sqrt{x}$	$\displaystyle {1 \over 2\, \sqrt{x}}$
$e\,^x$	$e\,^x$
$e\,^{k\,x}$	$k\cdot e\,^{k\,x}$
$C\cdot e\,^{k\,x}$	$C\cdot k\cdot e\,^{k\,x}$
$a\,^x$	$a\,^x \cdot \ln a$
$C\cdot a\,^{k\,x}$	$C\cdot k\cdot a\,^{k\,x} \cdot \ln a$
$a\cdot f(x)$	$a\cdot f\,'(x)$
$f(x) + g(x)\,$	$f\,'(x) + g\,'(x)$

De två sista raderna i tabellen är snarare generella satser än deriveringsregler. De gäller för alla funktioner $f(x)\,$ och $g(x)\,$. Av praktiska skäl tar vi upp dem ändå i samma tabell som deriveringsreglerna.

Denna tabell kommer att kompletteras i Matte 4-kursen då vi kommer att lära oss ytterligare deriveringsregler: regler för derivatan av en produkt resp. kvot av funktioner, den s.k. Produkt- resp. Kvotregeln samt deriveringsregeln för sammansatta funktioner, den s.k. Kedjeregeln.

Copyright © 2020 TechPages AB. All Rights Reserved.