1.4 Talet e och den naturliga logaritmen

<<  Förra demoavsnitt

Genomgång

Övningar

Nästa demoavsnitt  >>

Talet  $e \,$

Experiment 1 $\qquad$ Ta fram din miniräknare och gör så här:

1. Leta efter funktionsknappen (ev. med hjälp av 2nd-knappen) $\quad \boxed{e^{\,x}} \;\;$
2. Tryck på den, mata in $\, 1 \,$ och stäng parentesen.
3. Tryck på ENTER när det står $\, e$ ^ $(1) \;$ i räknarens display.

Du har beräknat $\; e{\,^1} \;$ eller talet $\, \color{blue} e \,$, dvs $\qquad 2,718281828\ldots \quad$,

en av matematikens mest kända konstanter, även kallad Eulers tal.

Talet $\, \color{blue} e \,$ är kallat efter den tysk-schweiziske matematikern Leonard Euler som på 1700-talet definierade detta märkliga tal.

Märkligt, därför att $\, e \,$ inte är ett "vanligt" tal som heltal eller bråk. Det är inte ett rationellt tal, se olika typer av tal.

Talet $\, e \,$ är ett irrationellt tal, precis som talen $\pi,\, \sqrt{2},\, \sqrt{3},\,\ldots \,$, som inte kan skrivas i bråkform.

Irrationella tal är decimaltal som har en icke-periodisk decimalutveckling dvs oändligt många decimaler utan något upprepande mönster (period).

Här kan man beskåda de första 5 miljoner decimaler av talet $\, e \,$. Leta gärna efter ett upprepande mönster! Du kommer inte att hitta något.

  OBS! $\quad e \;$ är ingen variabel utan en s.k. namngiven konstant som har värdet $\, 2,718281828\ldots \,$.

Talet $\, e \,$ förekommer bl.a. i en formel som enligt många är en av matematikens vackraste, nämligen sambandet mellan heltalet $1\,$, de irrationella talen $e,\;\pi$ och den imaginära enheten $\, i = \sqrt{-1}$, där även $\pi$ och $\, i \,$ är namngivna konstanter:

$e^{\,2\,\pi\,i}$ $= 1$

Ingen fara, vi har inte för avsikt att närmare gå in på denna formel. Vi nämner den bara för att illustrera betydelsen av talet $\, e \,$ inom den matematiska analysen, den delen av matematiken som behandlar gränsvärden, derivator, integraler och differentialekvationer.

Hur kom(mer) talet $e \,$ till?

Eulers formel kan användas för att numeriskt få fram några decimaler av talet $e \,$:

$\left(1 + {1 \over n}\right)^n \to \; e$ $\quad {\rm när} \quad n \to \infty$

Dvs: Uttrycket ovan går mot $e \,$ när $n\,$ går mot oändligheten ($\infty$) eller:

Uttrycket närmar sig allt mer $\, e \,$ ju större $\, n\,$ blir. Tabellen tar några steg i denna process:

$n$	$1\,000$	$1000\,000$	$1000\,000\,000$	$10\,000\,000\,000$	$\to \infty$
$\left(1 + {1 \over n}\right)^n$	${\color{Red} {2,71}}6923932\ldots$	${\color{Red} {2,71828}}0469\ldots$	${\color{Red} {2,71828182}}7\ldots$	${\color{Red} {2,718281828\ldots}}$	$\quad \to \; {\color{Red} {{\rm Eulers\;tal\;} e}} \quad$

De korrekta siffrorna är rödmarkerade och visar hur uttrycket sakta men säkert konvergerar mot det värde man får i räknaren när man slår in $e^{\,1} \,$.

Eulers formel ger oss en algoritm för att med hjälp av heltalen $\, n \,$ närma oss det irrationella talet $\, e \,$ (tabellen ovan).

Så i fortsättningen när vi räknar med talet $e \,$ nöjer vi oss med följande närmevärde med nio decimaler:

$e \; = \; {\color{Red} {2,718281828\ldots}}$

Exponentialfunktionen med basen $e \,$

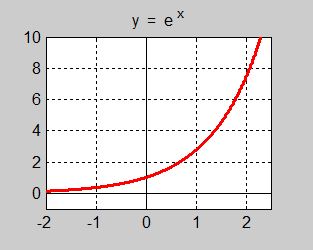
Tar man talet ${\color{Red} e}$ som bas och bildar potensen ${\color{Red} {e{\,^x}}}$ får man den s.k. exponentialfunktionen ${\color{Red} {y = e{\,^x}}}$ med basen ${\color{Red} e} \,$ som har stor betydelse inom naturvetenskap, teknik och ekonomi:

$y \; = \; e\,^x$

      med grafen:       

Exponentialfunktionen med basen $\; {\color{Red} e}$

Egenskaper

1. Exponentialfunktionen är alltid positiv: $\, e\,^x \, > \, 0 \,$ för alla $\, x$. Den blir aldrig $0\,$ eller negativ. Definitionsmängden: alla $x$.
2. $e\,^0 = 1$ vilket följer av potenslagen om nollte potens.
3. För negativa $\, x \,$ är $\, e\,^x < 1$. För positiva $\, x \,$ är $\, e\,^x > 1$ och växer allt starkare ju större $\, x \,$ blir.
4. Exponentialfunktionen växer starkast bland alla (hittills för oss kända) matematiska funktioner.

Exponentiell tillväxt modelleras med exponentialfunktioner av typ $\, y = C \cdot e\,^{k \, x} \,$ med $\, k \, {\color{Red} >} \, 0$.

Exponentiell minskning modelleras med exponentialfunktioner av typ $\, y = C \cdot e\,^{k \, x} \,$ med $\, k \, {\color{Red} <} \, 0$.

Exponentiell tillväxt (eller minskning) förekommer både i naturvetenskapliga och ekonomiska tillämpningar. Den har en starkare takt än t.ex. potensfunktionen $\, y = x^2 \,$ som har kvadratisk tillväxt. Testa gärna genom att rita grafen till $\, y = x^2 \,$ och $\, y = e\,^x \,$ i ett och samma koordinatsystem och jämföra kurvornas branthet.

I repetitionen Exponentialfunktioner hade vi pratat om exponentialfunktioner (i pluralis) därför att vi där inte hade valt en speciell bas. Vilken exponentialfunktion man menar beror på vilken bas man väljer, t.ex. $y = 2\,^x$ eller $y = 3\,^x,\;\cdots$.

När man däremot pratar om den exponentialfunktionen (i singularis) utan att nämna basen menar man alltid exponentialfunktionen med basen $\, e\,$ $-$ som en slags prototyp för alla exponentialfunktioner.

Den naturliga logaritmen

Experiment 2 $\qquad$ Ta fram din miniräknare och gör så här:

1. Tryck på funktionsknappen $\, \boxed{e^{\,x}}$ och mata in $\quad \color{Red}{\boxed{2}} \quad$ och stäng parentesen.
2. Tryck på ENTER när det står $\, e$ ^ $(2) \;$ i displayen. Låt resultatet $\, e^{\,2} \,$ (något decimaltal) stå i displayen.
3. Tryck på funktionsknappen $\, \boxed{\rm{LN}} \,$.
4. Mata in ANS som står för ANSwer och lagrar räknarens sist beräknade värde, i vårt fall $\, e^{\,2}$.
5. Stäng parentesen och tryck på ENTER: Du får tillbaka $\quad \color{Red}{\boxed{2}} \quad$ som du hade matat in i början.

Du har beräknat $\, \ln\,(e^{\,2})$ som ger $\, 2 \,$, dvs: $\qquad\quad\;\;\; \ln\,(e^{\,2}) \, = \, 2$

Genomför ett liknande experiment som visar: $\qquad\qquad e^{\,\ln 2} \, = \, 2 \,$

I räknaren står $\boxed{\rm{LN}}$ för Logaritmus Naturalis, den naturliga logaritmen, medan $\boxed{\rm{LOG}}$ står för $\, 10$-logaritmer.

När man skriver står $\ln$ för logaritmus naturalis och är symbolen för den naturliga logaritmen.

Talet $\, e \,$ bildar basen till $\ln$.

Exempel:

$\ln 3 \,$ = Exponent som basen $\, e \,$ ska upphöjas till, för att ge $\, 3 \,$:

$\quad e\,^{\color{Red} {1,09861\ldots}} \; = \; 3 \qquad \Leftrightarrow \qquad {\color{Red} {1,09861\ldots}} \; = \; \ln\,3$

---

I räknaren: $\qquad\qquad\quad \boxed{\text{LN}}$ $(3) \; = \; {\color{Red} {1,09861\ldots}}$

Generellt:

Definition:

$\ln a \,$ = Exponenten $\color{Red} x$ som basen $\, e \,$ ska upphöjas till, för att ge $\, a \,$:

$\qquad\qquad\quad$ $e^{\color{Red} x} = a \qquad \Leftrightarrow \qquad {\color{Red} x} = \ln\,a$

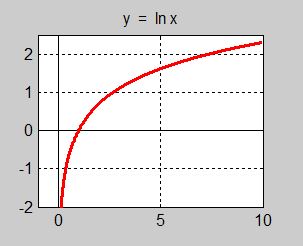
Exponentialfunktionen $\, y = e\,^x \,$ ger upphov till den naturliga logaritmfunktionen $\, {\color{Red} {y = \ln x}} \,$:

$y \; = \; \ln\, x$

      med grafen:       

Den naturliga logaritmfunktionen

Egenskaper

1. Logaritmen är definierad endast för positiva $\, x\,$. Definitionsmängden: $\, x > 0$.
2. $\ln\,1 = 0 \,$ vilket är logaritmformen till $\, e\,^0 = 1$, se egenskap 2 hos exponentialfunktionen.
3. För $x < 1\,$ är logaritmen negativ och för $x > 1\,$ är den positiv.
4. Logaritmen växer allt svagare ju större $\, x\,$ är.

  OBS!   Logaritmen är för $\, x=0 \,$ inte alls och för $\, x<0 \,$ inte definierad inom de reella talen.

För $\, x < 0 \,$ har $\, y \, = \, \ln x \,$ komplexa värden.

Här behandlas den naturliga logaritmen endast inom de reella talen.

Inversegenskapen

Experiment 2 visar ett exempel på att $\, \boxed{\rm{LN}} \,$ är den inversa operationen till $\, \boxed{e\,^x} \,$.

Generellt:

Den naturliga logaritmen $\, y \, = \, \ln\,x \,$ är den inversa (motsatta) funktionen till exponentialfunktionen $\, y \, = \, e\,^x \,$:

$$\ln\,(e^{\,x}) \, = \, x \qquad {\rm och\; } \qquad e^{\,\ln\,x} \, = \, x \qquad\quad {\rm I\;ord:\quad } e^{\,x} {\rm \;och\; } \ln\,x \;{\rm {\color {Red} {tar\;ut\;varandra}}.}$$

Inversegenskapen gäller oberoende av operationernas ordning: Vare sig du tar först $e^{\,x}$ och sedan $\ln\,x$ eller tvärt om, resultatet blir alltid $\,x$.

Dvs man återvänder till det värde $\,x$ man hade börjat att använda någon av dessa operationer på. Förutsättningen är förstås att man utför $e^{\,x}$ och $\ln\,x$ direkt efter varandra.

Både $\ln\,(e^{\,x})$ och $e^{\,\ln\,x}$ är exempel på s.k. sammansatta funktioner. För sådana funktioner gäller regeln:

Sammansatta funktioner beräknas inifrån: Experiment 2 var ett exempel på detta. För att få $\, \ln\,(e^{\,2}) \,$, beräknades först $\, e^{\,2}$ och sedan $\, \ln\,(e^{\,2})$.

Exponentialekvationen av typ $\; e\,^x \, = \, b$

Precis som exponentialekvationen $\, 10\,^x \, = \, b \;$ löstes med den inversa operationen till $\, 10\,^x$, nämligen $\, 10$-logaritmen, löses ekvationen ovan med den inversa operationen till $\, e\,^x$, nämligen den naturliga logaritmen.

Exempel

$\begin{array}{rcll} e^{\,x} & = & 68 & {\rm Logaritmera\;båda\;leden\;med\;\ln} \\ {\color{Red} {\ln}}\,({\color{Red} e}^{\,x}) & = & \ln\,68 & {\rm Använd\;inversegenskapen\;på\;VL} \\ x & = & \ln\,68 & \\ x & = & 4,219507705\ldots & \\ {\rm Kontroll:\qquad} e^{\,4,219507705} & = & 68 & \end{array}$

Internetlänkar

https://www.youtube.com/watch?v=X-z0aw_q7yM

http://www.youtube.com/watch?v=Z3xsdOvjl4E

http://www.youtube.com/watch?v=_FZJiyqIrG4&feature=related

http://www.youtube.com/watch?v=7RAWXVoyls4

Copyright © 2019 TechPages AB. All Rights Reserved.