3.3 Terasspunkter

Genomgång

Även i detta avsnitt antar vi att alla behandlade funktioner \( \; y \, = \, f(x) \; \) skall vara kontinuerliga i alla punkter av det betraktade området.

Vad är en terasspunkt?

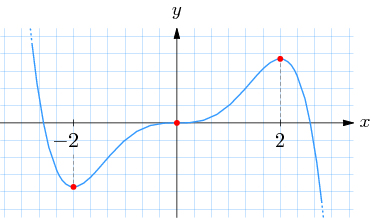Bilden till vänster visar tre punkter där kurvan har tangenter med lutningen \( \, 0 \):

Ett minimum i \( \quad\;\, x = -2 \, \)

En terasspunkt i \( \, x = 0 \, \)

Ett maximum i \( \quad\, x = 2 \, \)

I minimipunkten \( \;\, x = -2 \, \) gäller: \( \, f\,'(-2) \, = \, 0 \quad {\rm och} \quad f\,''(-2) \, > \, 0 \), se reglerna.

I terasspunkten \( \, x = 0 \quad \) gäller: \( \, f\,'(0) \quad = \, 0 \quad {\rm och} \quad f\,''(0) \quad {\color {Red} =} \;\; 0 \).

I maximipunkten \( \, x = 2 \quad \) gäller: \( \, f\,'(2) \quad = \, 0 \quad {\rm och} \quad f\,''(2) \;\; < \;\, 0 \), se reglerna.

Regeln om terasspunkt med derivator

\( f\,'(a) \, = \, f\,''(a) \, = \, 0 \; \) och \( \; f\,'''(a) \, \neq \, 0 \quad \Longrightarrow \quad \) Funktionen \( \; y = f(x) \; \) har en terasspunkt i \( \; x = a \; \).

Om \( \; f\,'(a) \, = \, f\,''(a) \, = \, f\,'''(a) \, = \, 0 \; \) kan ett teckenstudium avgöra den kritiska punktens typ.

Med andra ord, i en terasspunkt måste första- och andraderivatan vara \( \, = 0 \), men tredjederivatan \( \, \neq 0 \).

Tredjederivatan är inget annat än andraderivatans derivata. Man får den genom att derivera andraderivatan en gång till enligt deriveringsreglerna.

Att tredjederivatan inte får vara \( \, 0 \, \) är ett nödvändigt villkor för att funktionen ska ha en terasspunkt.

Kritiska punkter

En punkt \( \, x = a \, \) kallas för kritisk punkt om \( \, f\,'(a) = 0 \, \).

En kritisk punkt kan vara ett maximum, ett minimum eller en terasspunkt.

Ett annat namn för kritiska punkter är stationära punkter. Stationära, därför att kurvan "stannar av" i dessa punkter, dvs lutningen är \( \, 0\): Kurvan är varken växande eller avtagande.

Exempel på terasspunkt med derivator

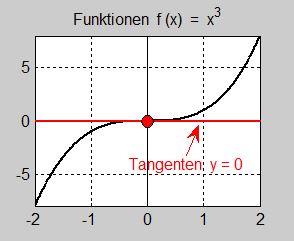
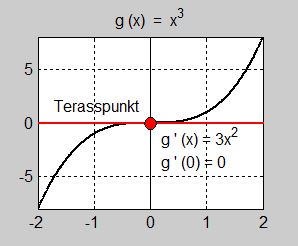
Undersök med derivator vilken typ av kritisk punkt funktionen \( \, f(x) = x\,^3 \, \) har i punkten \( \, x = 0 \, \).

Lösning med derivator:

\[\begin{array}{rclclcl} f(x) & = & x\,^3 & & \\ f'(x) & = & 3\,x\,^2 & \Longrightarrow & f'(0) = 3\cdot 0^2 = 3\cdot 0 & = & 0 \\ f''(x) & = & 6\,x & \Longrightarrow & f''(0) = 6\cdot 0 & = & 0 \\ f'''(x) & = & 6 & \Longrightarrow & f'''(0) = 6 & \neq & 0 \end{array}\]

Vi ser att \( \, f\,'(0) = f\,''(0) = 0 \, \) och \( \, f\,'''(0) \neq 0 \). Av regeln ovan följer att \( \, f(x)\, \) har en terasspunkt i \( \, x = 0 \, \) som visas på bilden till vänster.

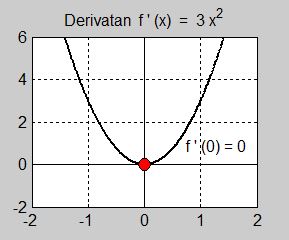
Bilden i mitten visar att derivatan har ett nollställe i \( \, x = 0 \, \). Det speciella med detta nollställe är att kurvan inte skär \( \, x\)-axeln utan endast berör den. Med andra ord, \( \, x = 0 \, \) är en dubbelrot till andragradsfunktionen \( \, f\,'(x) = 3\,x^2 \, \). Detta innebär att derivatan inte byter tecken kring \( \, x = 0 \, \) dvs är positiv både till vänster och till höger om nollstället. Att derivatan är positiv på båda sidor av sitt nollställe innebär i sin tur att själva funktionen \( \, f(x) = x^3 \, \) är växande både till vänster om och till höger om \( \, x = 0 \, \) \(-\) vilket är ett kännetecken för terasspunkter. En annan konsekvens av derivatans dubbelrot är att andraderivatan är \( \, 0 \, \) i \( \, x = 0 \, \):

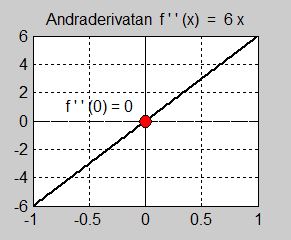
Bilden till höger visar att även andraderivatan är \( \, 0 \, \) i \( \, x = 0 \, \). Till skillnad från derivatans nollställe är detta nollställe av enkel typ, vilket framgår av att grafen verkligen skär \( \, x\)-axeln dvs byter tecken kring \( \, x = 0 \, \). I självaste punkten \( \, x = 0 \, \) är andraderivatan varken positiv eller negativ, varav följer att \( \, x = 0 \, \) inte är någon extrempunkt för funktionen \( \, f(x) = x^3 -\) ytterliare ett kännetecken för terasspunkter. En annan konsekvens av att andraderivatans rot är av enkel typ är att tredjederivatan är \( \, \neq 0 \, \) i \( \, x = 0 \, \).

Alternativt till användning av derivator finns det alltid möjligheten att genomföra ett teckenstudium för att känna igen en terasspunkt:

Regeln om terasspunkt med teckenstudium

\( f\,'(a) = 0 \; \) och \( \; f\,'(x) \) inte byter tecken kring \( \, x=a \quad \Longrightarrow \quad \) Funktionen \( \; y = f(x) \; \) har en terasspunkt i \( \; x = a \; \).

Med andra ord, i en terasspunkt \( \, x=a \) måste derivatan vara \( \, 0 \), utan att byta tecken kring \( \, a \), dvs derivatan är antingen positiv eller negativ på båda sidor av \( \, x=a \).

Exempel på terasspunkt med teckenstudium

Undersök med teckenstudium vilken typ av kritisk punkt funktionen \( \, f(x) = x\,^3 \, \) har i punkten \( \, x = 0 \, \).

Lösning med teckenstudium:

Vi hade redan bestämt att

derivatan var \( \, 0 \) för \( \, x = 0 \, \):

\[ f(x) = x^3 \]

\[ f'(x) = 3\,x^2 \]

\[ f'(0) = 3\cdot 0^2 = 3\cdot 0 = 0 \]

Nu ska vi undersöka derivatans tecken till vänster och till höger om nollstället \( \, x = 0 \).

Vi väljer t.ex. punkterna \( \, x = -0,1 \) och \( \, x = 0,1 \) och bestämmer derivatans tecken i dessa punkter:

\[ f' (-0,1) = 3\cdot (-0,1)^2 = 3\cdot 0,01 = 0,03 > 0 \]

\[ f' (0,1) = 3\cdot (0,1)^2 = 3\cdot 0,01 = 0,03 > 0 \]

\(x\)	\(-0,1\)	\(0\)	\(0,1\)
\( f\,'(x) \)	\(+\)	\(0\)	\(+\)
\( \,f(x) \)	↗	Terass	↗

Dessa resultat är infogade i teckentabellen till höger som visar:

\( \, f\,'(0) = 0 \, \)
Derivatan har tecknet \(+\) till vänster och även \( + \) till höger om \( \, 0 \, \) dvs derivatan byter inte tecken kring sitt nollställe.

Enligt regeln om terasspunkt med teckenstudium drar vi slutsatsen att funktionen \( f(x)\, \) har en terasspunkt i \( \, x = 0 \).

Avgörande för att teckenstudium är en korrekt algebraisk metod är förutsättningen vi gjorde inledningsvis, nämligen att \( \; y \, = \, f(x) \; \) är kontinuerlig i alla punkter av det betraktade området.

Hur grafen kan lura oss

Har funktionen

\[ f(x) = x^3 + \, 0,5\,x \]

vars graf visas till vänster en terasspunkt i \( \, x = 0 \, \)?

Kurvan är av samma typ som \( g(x) = x^3 \) till höger.

Ritar man båda funktioners grafer i miniräknarens

display är det svårt att se skillnaden. Slutsatsen att

även \( f(x) \) har en terasspunkt i \( x = 0 \) ligger nära.

Men \( f\,'(0) \neq 0 \) visar att detta inte är fallet:

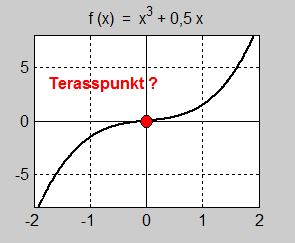
\[\begin{array}{rcl} f(x) & = & x^3 + \, 0,5\,x \\ f'(x) & = & 3\,x^2 + \, 0,5 \\ f'(0) & = & 3\cdot 0^2 + \, 0,5 = 3\cdot 0 \, + \, 0,5 = 0 \, + \, 0,5 \, = \, 0,5 \, \neq \, 0 \end{array}\]

Dvs redan första kravet i regeln om terasspunkt med derivator, nämligen att derivatan ska vara \( \, 0 \, \) för \( \, x = 0 \, \) är inte uppfyllt: \( \, f(x) \, \) har ingen terasspunkt i \( \, x = 0 \, \). Grafen har lurat oss.

Vill man använda grafer borde man först undersöka funktionen med de strikta algebraiska reglerna och sedan rita grafer för att visualisera resultatet. I det här fallet är det lämpligt att även rita tangenten till \( \, f(x) \, \) i \( \, x = 0 \, \). Lägger man till graferna till derivatan och andraderivatan får man en fullständig överblick över funktionens beteende i och kring \( \, x = 0 \, \):

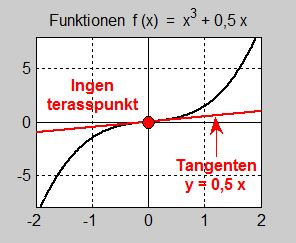
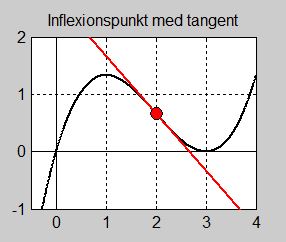
Bilden till vänster visar funktionens graf samt tangenten till kurvan i \( \, x = 0 \). Tangenten är inte horisontell dvs har inte lutningen \( \, 0 \). I beräkningen ovan hade vi fått: \( f'(x) = 0,5 \neq 0 \). Därmed är även tangentens lutning \( \, 0,5 \, \) och dess ekvation: \( y = 0,5\,x \). Därför föreligger i \( \, x = 0 \, \) inte en terasspunkt.

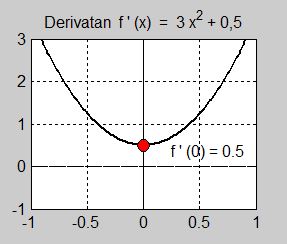
Bilden i mitten visar att derivatan inte har något nollställe vilket visar att funktionen varken har extrempunkter eller terasspunkter. Derivatan är alltid positiv och antar i \( x = 0 \) värdet \( \, 0,5 \, \). Om detta värde hade varit \( \, 0 \, \) hade funktionen haft en terasspunkt i \( x = 0 \).

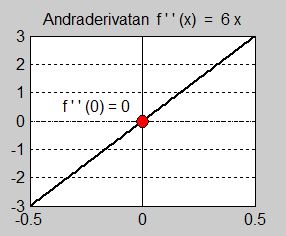
Bilden till höger visar att andraderivatan har ett nollställe i \( \, x = 0 \, \), där grafen skär \( \, x\)-axeln. Vad innebär detta? Vi har inte haft ett sådant fall där derivatan är skild från \( \, 0 \, \), men andraderivatan är \( \, 0 \, \). Därför handlar det om en speciell punkt på kurvan som varken är extrem- eller terasspunkt, för i dessa fall borde ju derivatan vara \( \, 0 \, \). Faktiskt handlar det om en ny typ av punkt som kallas inflexionspunkt.

Inflexionspunkter

Om du föreställer dig att du kör bil på S-kurvan på bilden till vänster,

svänger du ratten först till höger tills du kommer till S-kurvans mitt:

\( \, x = 2 \, \). Sedan byter du svängriktning och rattar till vänster.

Punkten i \( \, x = 2 \, \) där du byter svängriktning kallas för inflexionspunkt.

Inflexionspunkter är sådana där kurvan går över från en högersväng

(konkav kurva) till en vänstersväng (konvex kurva) eller tvärtom \(-\)

allt sett från vänster och underifrån.

På bilden finns även tangenten ritad i \( \, x = 2 \, \) vars lutning är negativ.

Hade lutningen varit \( \, 0 \, \) hade \( \, x = 2 \, \) varit en terasspunkt. Därför:

Terasspunkter är specialfall av inflexionspunkter, eftersom kurvan byter alltid svängriktning i en terasspunkt.

Men inte alla inflexionspunkter är terasspunkter. Inflexionspunkter kan ha tangenter med vilken lutning som helst.

Terasspunkter är sådana inflexionspunkter där tangenten har lutningen \( \, 0 \, \).

Pga funktionens kontinuitet finns alltid en inflexionspunkt mellan två extrempunkter.

Regeln om inflexionspunkter

\( f\,''(a) \, = \, 0 \; \) och \( \; f\,'''(a) \, \neq \, 0 \; \quad \Longrightarrow \quad \) Funktionen \( \; y \, = \, f(x) \; \) har en inflexionspunkt i \( \; x = a \; \).

Om dessutom \( \; f\,'(a) \, = \, 0 \; \) är \( \; x = a \; \) en terasspunkt. (Samma som tidigare)

En terasspunkt är alltid en inflexionspunkt, men inte tvärtom.

För att hitta inflexionspunkter ställer man alltså upp andraderivatan, sätter den till \( \, 0 \, \) och beräknar\( \, x \), dvs andraderivatans nollställen. Sedan kontrollerar man om tredjederivatan verkligen är skild från \( \, 0 \, \) för andraderivatans nollställen.

Dessutom gäller det: Om \( \, f\,'''(a) > 0 \, \) är kurvan konkav i \( \, x = a \ ,\) och vi har en övergång från höger- till vänstersväng \(-\) som i grafen ovan. Om däremot \( \, f\,'''(a) < 0 \, \) är kurvan konvex i \( \, x = a \ ,\) och kurvan går över från en vänster- till en högersväng.