Potenser
| <-- Till Polynom | Genomgång | Övningar |
Hur räknar du?
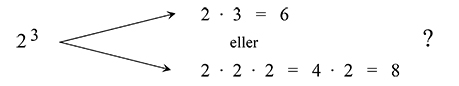 \[ {\rm {\color{Red} {OBS!\quad Vanligt\,fel:}}} \quad\; 2\,^3 \; = \; 6 \]
\[ {\rm {\color{Red} {OBS!\quad Vanligt\,fel:}}} \quad\; 2\,^3 \; = \; 6 \]
\[ \qquad\quad\;\, {\rm Rätt:} \qquad\qquad\! 2\,^3 \; = \; 2 \cdot 2 \cdot 2 \; = \; 4 \cdot 2 \; = \; 8 \]
Det vanliga felet beror på att man blandar ihop två olika räkneoperationer: multiplikationen med att ta upphöjt till.
Hjärnan associerar \( \, 2 \, \) och \( \, 3 \, \) till multiplikationstabellen och väljer blind \( \, 6 \, \). I själva verket är \( \, 2\,^3 \, \) ingen produkt utan en potens.
Potensbegreppet
Ett uttryck av formen \( \, a\,^x \, \) läses \( \, {\color{Red} a} \) upphöjt till\( \, {\color{Red} x} \, \) och kallas för potens. \( \, a\, \) heter basen och \( \, x \, \) exponenten.
Om exponenten \( \, {\color{Red} x} \, \) är ett positivt heltal och basen \( a\, \) ett tal \( \neq 0 \) kan potensen \( \, a^{\color{Red} x} \, \) definieras som:
- \( a^{\color{Red} x} = \underbrace{a \cdot a \cdot a \cdot \quad \ \cdots \quad \cdot a}_{{\color{Red} x}\;\times} \)
Så \( \, 2\,^{\color{Red} 3} \, = \, 2 \cdot 2 \cdot 2 \, \) kan uppfattas som en förkortning för upprepad multiplikation av \( 2\, \) med sig själv, \( \, {\color{Red} 3} \, \) gånger (jfr. upprepad addition).
Exempel:
- \( a^2 = a \cdot a \)
- \( a^3 = a \cdot a \cdot a \)
Om vi nu multiplicerar dessa två potenser med varandra och använder potensens definition, får vi:
- \( a^2 \cdot a^3 \; = \; \underbrace{a \cdot a}_{2\;\times} \; \cdot \; \underbrace{a \cdot a \cdot a}_{3\;\times} \; = \; \underbrace{a \cdot a \cdot a \cdot a \cdot a}_{{\color{Red} 5}\;\times} \; = \; a^{\color{Red} 5}\)
Vi kan sammanfatta till:
- \( a^2 \cdot a^3 \; = \; a^{2+3} = \; a^5\)
Detta är ett exempel på en allmän lag, den första potenslagen. Det finns flera sådana:
Potenslagarna
Följande lagar gäller för potenser där basen \( a\, \) är ett tal \( \neq 0 \), exponenterna \( \, x \, \) och \( \, y \, \) rationella tal (bråktal) och \( m,\,n \) heltal (\( n\neq 0 \)):
Första potenslagen: \( \qquad\qquad\quad\;\, a^x \cdot a^y \; = \; a\,^{x \, + \, y} \qquad\qquad \)
Andra potenslagen: \( \qquad\qquad\qquad\quad \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \qquad\qquad \)
Tredje potenslagen: \( \qquad\qquad\qquad \displaystyle {(a^x)^y} \; = \; a\,^{x \, \cdot \, y} \qquad\qquad \)
Lagen om nollte potens: \( \qquad\qquad\qquad\! a\,^0 \; = \; 1 \qquad\qquad \)
Lagen om negativ exponent: \( \qquad\qquad a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad\qquad \)
Lagen om rationell exponent: \( \qquad\qquad a^{m \over n} \; = \; \sqrt[n]{a^m} \qquad\qquad \)
Specialfall \(m=1\) (\(n\)-te roten): \( \qquad\qquad a^{1 \over n} \; = \; \sqrt[n]{a} \qquad\qquad \)
För enkelhets skull definierades potensbegreppet inledningsvis endast för positiva heltalsexponenter \( \, x \, \) och \( \, y \). Men potenslagarna gäller även för negativa och rationella exponenter som behandlas längre fram. I Lagen om negativ exponent antas \( \, x > 0 \).
Bevis(idéer) av några potenslagar
Påstående (Första potenslagen):
- \( a^x \cdot a^y \; = \; a\,^{x \, + \, y} \)
Bevisidé:
Påståendet kan bevisas genom att använda potensens definition:
- \( a^{\color{Red} x} \cdot a^{\color{Red} y} \; = \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} x}\;\times} \; \cdot \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} y}\;\times} \; = \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} {x+y}}\;\times} \; = \; a^{{\color{Red} {x+y}}} \)
Påstående (Andra potenslagen):
- \( \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \)
Bevisidé:
Potensens definition ger:
- \( \displaystyle {a^{\color{Red} x} \over a^{\color{Red} y}} \; = \; \displaystyle {\overbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}^{{\color{Red} x}\;\times} \; \over \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} y}\;\times}} \; = \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} {x-y}}\;\times} \; = \; a^{{\color{Red} {x-y}}} \)
Det sista bråket har förkortats så mycket som möjligt.
Exempel:
- \( \displaystyle {a\,^5 \over a\,^3} \; = \; {a \cdot a \cdot a \cdot a \cdot a \; \over \; a \cdot a \cdot a} \; = \; a \cdot a \; = \; a\,^2 \)
Det sista bråket har förkortats med \( \, a \cdot a \cdot a \). Vi kan sammanfatta till:
- \( \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; a\,^{{\color{Red} {5-3}}} \; = \; a\,^2 \)
Påstående (Lagen om nollte potens):
- \( a^0 \; = \; 1 \)
Bevis:
Påståendet kan bevisas genom att använda andra potenslagen:
- \( \displaystyle{a^x \over a^x} \; = \; a^{x-x} \; = \; a^0 \)
Å andra sidan vet vi att ett bråk med samma täljare som nämnare har värdet \( \, 1 \):
- \( \displaystyle{a^x \over a^x} \; = \; 1 \)
Av raderna ovan följer påståendet:
- \( a^0 \; = \; 1 \)
Potenser med negativa exponenter
Påstående (Lagen om negativ exponent):
- \( a^{-x} = \displaystyle{1 \over a^x} \)
Bevis:
Påståendet kan bevisas genom att använda den ovan bevisade lagen om nollte potensen (baklänges) samt andra potenslagen:
- \( \displaystyle{1 \over a^x} \; = \; \displaystyle{a^0 \over a^x} \; = \; a^{0-x} \; = \; a^{-x} \)
Vi får påståendet, fast baklänges.
Exempel på potenser med negativa exponenter
- \[ \;\; a^{-1} = {1 \over a^1} = {1 \over a} \]
- \[ \;\; a^{-2} = {1 \over a^2} = {1 \over a \cdot a} \]
- \[ \;\; a^{-3} = {1 \over a^3} = {1 \over a \cdot a \cdot a} \]
Att potenser med negativa exponenter är en naturlig fortsättning på potenser med positiva exponenter med nollte potensen däremellan illustrerar följande exempel:
Varför är \( \; 5\,^0 \, = \, 1 \; \)?
- \[ \;\; 5^4 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \cdot 5 \]
- \[ \;\; 5^3 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \]
- \[ \;\; 5^2 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \]
- \[ \;\; 5^1 \; = \; {\color{Red} 1} \cdot 5 \]
- \[ \;\; {\color{Red} {5^0 \; = \; 1}} \]
- \[ \;\; 5^{-1} \; = \; \displaystyle{{\color{Red} 1} \over 5} \]
- \[ \;\; 5^{-2} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5} \]
- \[ \;\; 5^{-3} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5} \]
- \[ \;\; 5^{-4} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5 \cdot 5 } \]
Att \( \; {\color{Red} 1} \)-orna följer med hela tiden beror på att multiplikationens enhet är \( \, {\color{Red} 1} \), dvs \( \, a \cdot {\color{Red} 1} \, = \, a \). Därför blir endast \( \, {\color{Red} 1} \, \) kvar, när vi kommer till \( \, {\color{Red} {5^0}} \, \) då alla \( \, 5\)-or har försvunnit.
Jämför med:
Varför är \( \; 5 \cdot 0 \, = \, 0 \; \)?
- \[ \;\; 5 \cdot 4 \; = \; {\color{Red} 0} + 5 + 5 + 5 + 5 \]
- \[ \;\; 5 \cdot 3 \; = \; {\color{Red} 0} + 5 + 5 + 5 \]
- \[ \;\; 5 \cdot 2 \; = \; {\color{Red} 0} + 5 + 5 \]
- \[ \;\; 5 \cdot 1 \; = \; {\color{Red} 0} + 5 \]
- \[ \;\; {\color{Red} {5 \cdot 0 \; = \; 0}} \]
- \[ \;\; 5 \cdot (-1) \; = \; {\color{Red} 0} - 5 \]
- \[ \;\; 5 \cdot (-2) \; = \; {\color{Red} 0} - 5 - 5 \]
- \[ \;\; 5 \cdot (-3) \; = \; {\color{Red} 0} - 5 - 5 - 5 \]
- \[ \;\; 5 \cdot (-4) \; = \; {\color{Red} 0} - 5 - 5 - 5 - 5 \]
Att \( \; {\color{Red} 0} \)-orna följer med hela tiden beror på att additionens enhet är \( \, {\color{Red} 0} \), dvs \( \, a + {\color{Red} 0} \, = \, a \). Därför blir endast \( \, {\color{Red} 0} \, \) kvar, när vi kommer till \( \, {\color{Red} {5 \cdot 0}} \, \) då alla \( \, 5\)-or har försvunnit.
Potenser med rationella exponenter
Potenser med rationella exponenter är bara ett annat sätt att skriva (högre) rötter.
Påstående (\( n\)-te roten):
- \( a^{1 \over n} \; = \; \sqrt[n]{a} \; \) \( , \qquad n\neq 0 \)
Bevisidé:
Vi tar specialfallet \( n=3 \), multiplicerar \( a \)\(^{1 \over 3} \) tre gånger med sig själv och använder potenslagen om produkt av potenser med samma bas:
- \( \displaystyle a^{1 \over 3} \cdot a^{1 \over 3} \cdot a^{1 \over 3} \; = \; a^{{1 \over 3} + {1 \over 3} + {1 \over 3}} \; = \; a^{3 \over 3} \; = \; a^1 \; = \; a \)
Definitionen för 3:e roten ur \( a \) är:
\( \qquad\quad \displaystyle \sqrt[3]{a} \; = \; \) Tal som 3 gånger multiplicerat med sig själv ger \( a \).
Men enligt ovan är det tal som 3 gånger med sig själv ger \( a \), just \( a \) \(^{1 \over 3} \). Alltså måste detta tal vara lika med 3:e roten ur \( a \):
- \( \displaystyle a^{1 \over 3} \; = \; \sqrt[3]{a} \)
Denna bevisidé kan vidareutvecklas till det allmänna fallet för alla heltal \( m\, \) och \( n\neq 0 \):
Påstående (Rationell exponent):
- \( a^{m \over n} \; = \; \sqrt[n]{a^m} \)
Potensekvationer
Anta i fortsättningen att \( \, x \, \) är en okänd variabel och \( b\, \) och \( c\, \) givna konstanter \( \neq 0 \) .
- Funktioner av typ \( y = x^3\, \) kallas potensfunktioner, generellt \( \; y = c \cdot x^b\, \).
- Ekvationer av typ \( x^3\, = 8 \) kallas potensekvationer, generellt \( \; x^b\, = c \).
I potensfunktioner och -ekvationer förekommer \( \, x \, \) i basen. Potensekvationer löses genom rotdragning. För t.ex. potensekvationen \( x^3\, = 8 \) finns det två olika sätt att beskriva lösningen via rotdragning:
- \[\begin{align} x^3 & = 8 \qquad & | \; \sqrt[3]{\;\;} \\ \sqrt[3]{x^3} & = \sqrt[3]{8} \\ x & = 2 \\ \end{align}\]
Alternativt (med rationell exponent):
- \[\begin{align} x^3 & = 8 \qquad & | \; (\;\;\;)^{1 \over 3} \; \text{samma som} \; \sqrt[3]{\;\;} \\ (x^3)^{1 \over 3} & = 8^{1 \over 3} \\ x^{3\cdot{1 \over 3}} & = 8^{1 \over 3} \\ x & = 2 \\ \end{align}\]
Det alternativa sättet att lösa ekvationen ovan visar att rötter även kan uppfattas och skrivas som potenser med rationella exponenter.
Internetlänkar
http://www.youtube.com/watch?v=iYgG4LUqXks
http://www.webbmatte.se/gym/arabiska/2/2_8_4sv.html
http://www.webbmatte.se/gym/arabiska/2/2_8_3sv.html
http://wiki.math.se/wikis/forberedandematte1/index.php/1.3_%C3%96vningar
Copyright © 2010-2015 Math Online Sweden AB. All Rights Reserved.