3.5 Lösning 8a

     Vi inför ett koordinatsystem och sätter glasskivan i det, så här:

+++

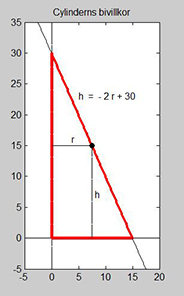
Vi inför ett koordinatsystem och sätter den röda triangeln från uppgiftens figur i den. Vi väljer Triangelns hypotenusa blir då en del av en rät linje. Vi väljer cylinders radie \( \, r \, \) som horisontell och dess höjd \( \, h \, \) Punkten \( \, (x, y) \, \) rör sig på denna räta linje vars ekvation är: \[ {\color{Red} y} \, = \, k\,x \, + \, m \] Lutningen \( \, k \, = \, \displaystyle {\Delta y \over \Delta x} \, = \, - \, {20 \over 30} \, = \, - \, {2 \over 3} \) Skärningspunkten med \(\,y\)-axeln: \( \quad m \, = \, 20 \) Den räta linjens ekvation blir då: \( \displaystyle {\color{Red} y} \, = \, - \, {2 \over 3}\,x \, + \, 20 \)

Detta samband mellan \( \, x \, \) och \( \, {\color{Red} y} \,\) är problemets bivillkor.