1.1 Lösning 5a

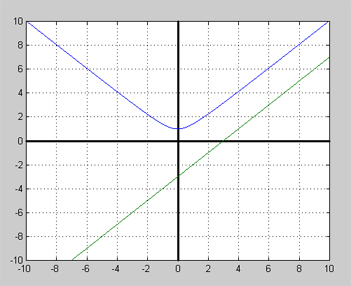
Lösningen av övning 4b visar graferna till \( y_1 = \sqrt{x^2 + 1} \) (blå kurva) och \( \displaystyle y_2 = x - 3 \) (grön linje):

Den räta linjens lutning är 1. Grafen visar att man behöver bara höja denna lutning för att få en skärningspunkt mellan kurvan och linjen. En höjning av lutningen till t.ex. 3 skulle räcka för en skärningspunkt. Därför borde följande rotekvation få en sann rot\[ \sqrt{x^2 + 1} = 3\,x - 3 \]

Lösningen\[\begin{align} \sqrt{x^2 + 1} & = 3\,x - 3 & & \qquad | \; (\;\;\;)^2 \\ x^2 + 1 & = (3\,x - 3)^2 & & \\ x^2 + 1 & = 9\,x^2 - 18\,x + 9 & & \qquad | \;\; - x^2 \\ 1 & = 8\,x^2 - 18\,x + 9 & & \qquad | \;\; - 1 \\ 0 & = 8\,x^2 - 18\,x + 8 & & \qquad | \;\; / 8 \\ 0 & = x^2 - 2,25\,x + 1 \\ x_{1,2} & = 1,125 \pm \sqrt{1,266 - 1} \\ x_{1,2} & = 1,125 \pm 0,515 \\ x_1 & = 1,64 \\ x_2 & = 0,61 \\ \end{align}\]

Prövning av \( x_1 = 1,64 \):

VL\[ \sqrt{1,64^2 + 1} = 1,92 \]

HL\[ 3\cdot 1,64 - 3 = 1,92 \]

VL = HL \( \Rightarrow\, x_1 = 1,64 \) är en sann rot.

Prövning av \( x_2 = 0,61 \):

VL\[ \sqrt{0,61^2 + 1} = 1,17 \]

HL\[ 3\cdot 0,61 - 3 = -1,17 \]

VL \(\not=\) HL \( \Rightarrow\, x_2 = 0,61 \) är en falsk rot.