1.5 Fördjupning till Kontinuerliga och diskreta funktioner
| <-- Förra avsnitt | Teori | Övningar | Fördjupning | Nästa avsnitt --> |
Lektion 8 Kontinuerliga & diskreta funktioner
Allmän definition
I teoridelen sade vi att kontinuerlig betydde sammanhängande (motsatsen till diskret).
Som exempel ritade vi grafen till en enkel linjär funktion med en genomdragen linje. Man kunde rita den utan att lyfta pennan. Vi kallade den kontinuerlig därför att dess definitionsmängd var kontinuerlig. Som exempel på kontinuerliga mängder nämnde vi de rationella och reella talen. Som ytterligare exempel på kontinuerliga funktioner nämndes polynomfunktionerna, se grafen där.
Allt detta är sant. Men förhållandena i tillämpningarna är ofta mer komplicerade än så. I vissa fall kan vi med verktygen ovan inte avgöra om en funktion är kontinuerlig. Vi behöver en exakt definition.
Diskreta funktioner är enkelt att identifiera: 1) Diskret definitionsmängd, i regel heltalen. 2) Åtskilda punkter som graf. Därför koncentrerar vi oss här på kontinuerliga funktioner.
Definition:
- En funktion \( y = f(x)\, \) är kontinuerlig för \( {\color{Red} x = a}\, \) om:
- \[ f(x) \to f(a)\, \] när \( x \to a \)
Den andra raden i definitionen läses\[ f(x)\, \] går mot \( f(a)\, \) när \( x\, \) går mot \( a\, \).
Observera att definitionen är punktvis, dvs den talar om när en funktion är kontinuerlig för ett visst \( {\color{Red} x}\, \)-värde nämligen för \( {\color{Red} x = a}\, \). Det finns ingen föreskrift för att avgöra om en funktion i sin helhet är kontinuerlig.
Exempel 1
Låt oss återuppta ett exempel som behandlades i Fördjupning till rationella uttryck nämligen funktionen:
- \[ y = {1 \over x} \]
Grafen ser ut så här:
a) Låt oss med hjälp av definitionen undersöka om den är kontinuerlig för \( {\color{Red} x = 0}\, \). Dvs vi ersätter i definitionen \( a \, \) med \( 0 \, \) och \( f(x) \, \) med \( 1 \over x \). Enligt definitionen borde då:
- \[ {1 \over x} \to f(0) \] när \( x \to 0 \).
Men \( {1 \over x} \) kan inte gå mot \( f(0)\, \) därför att \( f(0)\, \) dvs \( {1 \over 0} \) inte är definierad. Därme är definitionens krav inte uppfyllt.
Slutsats: Funktionen \( y = {1 \over x} \) är inte kontinuerlig för \( x = 0\, \).
b) Låt oss nu undersöka om funktionen är kontinuerlig för \( {\color{Red} x = 2}\, \). Vi ersätter i definitionen \( a \, \) med \( 2 \, \) och \( f(x) \, \) med \( 1 \over x \). Enligt definitionen borde då:
- \[ {1 \over x} \to {1 \over 2} \] när \( x \to 2 \).
Närmar man sig \( 2\, \) på \( x\, \)-axeln, från höger eller från vänster, närmar sig \( y\, \) värdet \( 1 \over 2 \) i båda fall, därör att \( f(2) = {1 \over 2} \). Därmed är dfinitionens krav uppfyllt.
Slutsats: Funktionen \( y = {1 \over x} \) är kontinuerlig för \( x = 2\, \).
På samma sätt kan man undersöka om funktionen är kontinuerlig för andra \( {\color{Red} x}\, \). Det kommer att visa sig att:
- Funktionen \( y = {1 \over x} \) är kontinuerlig för alla \( x \neq 0\, \).
Exempel 2
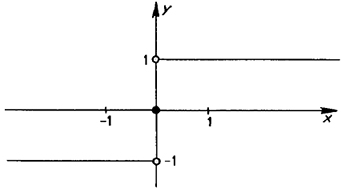
Inom datateknik används en funktion som heter Heavisidefunktionen och har följande graf:
De ihåliga ringarna vid \( y = 1 \, \) och \( y = -1 \, \) betyder att dessa värden inte tillhör funktionens värdemängd, medan den ifyllda ringen vid origo innebär att detta värde tillhör värdemängden.
Grafen visar en signal vars amplitud skiftar från 0 till 1 - en egenskap som liknar impulserna inom datornätverk med ettor och nollor. Funktionens skapare Oliver Heaviside använde den för att modellera strömmen genom elektriska kretsar.
Heavisidefunktionen definieras genom:
- \[ H(x) \, = \, \begin{cases} -1 & \mbox{om } x < 0, \\ 0 & \mbox{om } x = 0, \quad x \;\mbox{reellt tal} \\ 1 & \mbox{om } x > 0. \end{cases} \]
Kanske kan formeln ovan samt grafen, inkl. de ihåliga och ifyllda ringarna, förstås bättre med följande förklaring:
- \[\begin{align} H(\mbox{negativa tal}) & = -1 \\ H(0) & = 0 \\ H(\mbox{positiv tal}) & = 1 \end{align}\]
Låt oss nu med hjälp av den allmänna definitionen för kontinuerliga funktioner undersöka om Heavisidefunktionen är kontinuerlig för \( {\color{Red} x = 0}\, \). Enligt definitionen borde då:
- \[ H(x) \to H(0) \] när \( x \to 0 \).
Närmar man sig \( 0\, \) på \( x\, \)-axeln från höger närmar sig \( H(x)\, \) värdet \( 1\, \). Närmar man sig \( 0\, \) från vänster närmar sig \( H(x)\, \) värdet \( -1\, \).
Men \( H(0) = 0\, \). Dvs \( H(x) \to 1\, \) och \( \to -1\, \) och inte mot \( H(0) = 0\, \), når \( x \to 0 \). Därmed är dfinitionens krav inte uppfyllt.
Slutsats: Funktionen \( H(x)\, \) är inte kontinuerlig för \( x = 0\, \).
+++
På samma sätt kan man undersöka om funktionen är kontinuerlig för andra \( {\color{Red} x}\, \). Det kommer att visa sig att:
- Funktionen \( H(x)\, \) är kontinuerlig för alla \( x \neq 0\, \).
Olika typer av diskontinuitet
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.