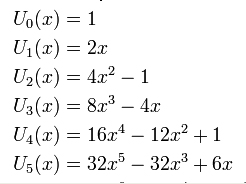1.1 Fördjupning till Polynom

Teori

Övningar

Fördjupning

Extrauppgifter

En familj av polynom

Ett polynoms grad är ett mått på dess kompexitet.

Ett exempel på hur kompexiteten växer med graden (från 0 till 5) är följande sex polynom vars grafer är ritade i samma koordinatsystem:

De nedsänkta indexen \(_0,\,_1,\,_2,\,_3,\,_4,\,_5\) i beteckningarna \(U_0, U_1, U_2, U_3, U_4, U_5\,\) används här både för att relatera indexet till polynomets grad och kunna skriva en formel för denna familj av polynom, vilket görs några rader längre fram.

Här följer graferna till polynomen ovan ritade i samma koordinatsystem:

Man ser att kurvorna får fler maxima/minima ju högre deras grad är.

Dessa polynom heter Chebyshevpolynom av 2:a slag efter den ryske matematikern Chebyshev som presenterade dem 1854. De är relaterade till varandra med följande formel, kallad rekursionsformel:

\[ U_n(x) = 2\,x\,\cdot\,U_{n-1}(x)\,-\,U_{n-2}(x) \qquad\qquad n = 2, 3, ... \]

\[ U_0(x) = 1, \quad U_1(x) = 2\,x \]

Om vi tittar på tabellen ovan ser man att polynomen \(U_n(x)\,\) bildar en följd där varje polynom har ett index n. Formeln ovan ger oss möjligheten att ta fram Chebyshevpolynomen successivt, dvs vi kan ställa upp ett polynom med hjälp av de två föregående. I princip kan man ställa upp alla Chebyshevpolynom med denna formel utgående från de två första som är givna. Låt oss börja med att ställa upp det tredje (OBS! n = 2) med hjälp av de två första (n = 0 och 1)\[ \displaystyle U_0(x) = \underline{1} \]

\( U_1(x) = \underline{2\,x} \)

För n = 2 ger formeln ovan\[ U_2(x) = 2\,x\,\cdot\,U_1(x)\,-\,U_0(x) = 2\,x\,\cdot\,2\,x\,-\,1 = \underline{4\,x^2\,-\,1} \]

Sedan kan vi få fram \( U_3(x) \) genom att att sätta in n = 3 i formeln ovan\[ U_3(x) = 2\,x\,\cdot\;U_2(x)\,-\,U_1(x) = 2\,x\,\cdot\,(4\,x^2\,-\,1)\,-\,2\,x = 8\,x^3\,-\,2\,x\,-\,2\,x = \underline{8\,x^3\,-\,4\,x} \]

För n = 4 ger formeln ovan \( U_4(x) \) osv.\[ U_4(x) = 2\,x\,\cdot\,U_3(x)\,-\,U_2(x) = 2\,x\,\cdot\,(8\,x^3\,-\,4\,x)\,-\,(4\,x^2\,-\,1) = 16\,x^4\,-\,8\,x^2\,-\,4\,x^2\,+\,1 = \underline{16\,x^4\,-\,12\,x^2\,+\,1} \]

Så här kan man fortsätta för att få fram alla Chebyshevpolynom. Eftersom formeln som används bygger på att beräkna ett polynom från de två föregående kallar man den för polymens rekursionsformel. Man kan säga att följden av Chebyshevpolynomen definieras och genereras av rekursionsformeln ovan.

Jämförelse av koefficienter

Jämförelse av koefficienter är en teknik eller en metod som används i olika sammanhang. Vi kommer att använda den för att i nästa avsnitt faktorisera polynom och med hjälp av faktorisering lösa ekvationer av högre grad än 2. Vi ska börja med att definiera likhet mellan polynom.

Med likhet mellan polynom menar man en algebraisk identitet mellan polynomen. Två polynom av samma grad:

\[ P(x) = a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad \ldots \quad + a_1 \cdot x + a_0 \]

och

\[ Q(x) = b_n \cdot x^n + b_{n-1} \cdot x^{n-1} + \quad \ldots \quad + b_1 \cdot x + b_0 \]

är lika med varandra om alla deras motsvarande koefficienter, dvs de som tillhör termer av samma grad, överensstämmer, närmare bestämt om:

\[ a_n = b_n, \quad a_{n-1} = b_{n-1}, \quad \ldots \quad a_1 = b_1, \quad a_0 = b_0 \]

Exempel 1

Två polynom är givna\[ P(x) = a \cdot x + 2\,a + b \]

\( Q(x) = 2\,x + 1\!\, \).

Låt \( a\, \) och \( b\, \) vara konstanter medan \( x\, \) är polynomens oberoende variabel.

För vilka värden på \( a\, \) och \( b\, \) är de två polymen lika med varandra?

Vi skriver \( P(x),\, \) och \( Q(x)\, \) så att vi lättare kan se motsvarande koefficienter\[ P(x) = a \cdot x^1 + (2\,a + b) \cdot x^0 \]

\( Q(x) = 2 \cdot x^1 + \quad\;\; 1 \quad\;\; \cdot x^0 \)

Jämförelse av koefficienterna till \( x^1\, \) leder till\[ a = 2\,\]

Jämförelse av koefficienterna till \( x^0 \,\) leder till\[ 2\,a + b = 1\!\,\]

Sätter man in \( a = 2\, \) i denna relation får man \( b = -3\, \).

Polynomen \( P(x)\, \) och \( Q(x)\, \) är lika med varandra för\[ a = 2\, \]

\( b = -3\, \)

Metoden kallas jämförelse av koefficienter och är ett viktigt verktyg för att lösa högre gradsekvationer genom att faktorisera högre gradspolynom, se övningarna 10 och 11.

Exempel 2

Problem: Följande 3:e gradspolynom är givet\[ P(x) = x^3 + 4\,x^2 + x - 26 \]

Hitta ett 2:a gradspolynom \( Q(x)\, \) så att:

\[ Q(x)\cdot (x-2) = P(x) \]

Svar: \( Q(x) = x^2 + 6 \, x + 13 \)

Lösning:

Det 2:a gradspolynomet \( Q(x)\, \) kan skrivas så här\[ Q(x) = a\,x^2 + b\,x + c \]

Vi bestämmer koefficienterna \( a\, , \, b\, \) och \( c\, \) så att \( Q(x)\cdot (x-2) = P(x) \)

\(\begin{align} Q(x) \cdot (x - 2) & = (a\,x^2 + b\,x + c)\cdot (x - 2) = a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c = \\ & = a\,x^3 + (b - 2\,a)\,x^2 + (c - 2\,b)\,x - 2\,c = \\ & = a \cdot x^3 + (b - 2\,a) \cdot x^2 + (c - 2\,b) \cdot x - 2\,c \cdot x^0 \\ P(x) & = 1 \cdot x^3 + \quad\;\; 4 \quad\;\; \cdot x^2 + \quad\;\; 1 \quad\;\; \cdot x - 26 \cdot x^0 \end{align} \)

Jämförelse av koefficienterna till \( x^3 \)-termen ger:

\[\begin{align} a & = 1 \end{align} \]

Jämförelse av koefficienterna till \( x^2 \)-termen ger:

\[\begin{align} b - 2\, a & = 4 \\ b - 2\cdot 1 & = 4 \\ b - 2 & = 4 \\ b & = 6 \\ \end{align} \]

Jämförelse av koefficienterna till \( x^1 \)-termen ger:

\[\begin{align} c - 2\, b & = 1 \\ c - 2\cdot 6 & = 1 \\ c - 12 & = 1 \\ c & = 13 \\ \end{align} \]

Jämförelse av koefficienterna till \( x^0 \)-termen bekräftar värdet på c:

\[\begin{align} - 2\,c & = - 26 \\ c & = 13 \\ \end{align} \]

Vi får \( a = 1\, , \, b = 6\, \) och \( c = 13\, \) och därmed\[ Q(x) = x^2 + 6 \, x + 13 \]