1.1 Lösning 6
- \[\begin{align} x^4 - 29\;x^2 & = -100 \\ x^4 - 29\;x^2 + 100 & = 0 \\ \end{align}\]
Vi inför en ny variabel z som vi definierar som:
- \[ \displaystyle z = x^2 \]
Denna substitution överför 4:e gradsekvationen till en 2:a gradsekvation:
- \[\begin{align} z^2 - 29\,z + 100 & = 0 \\ z_{1,2} & = 3 \pm \sqrt{9 + 27} \\ z_{1,2} & = 3 \pm 6 \\ z_1 & = 9 \\ z_2 & = - 3 \\ \end{align}\]
Övergången från z till x gör vi genom att först sätta in lösningen \( z_1 = 9 \) i substitutionen \( z = x^2 \):
- \[ \displaystyle z = x^2 = 9 \]
Nu drar vi roten ur båda leden i ekvationen \( x^2 = 9 \) och får lösningarna:
- \[ x_{1,2} = \pm 3 \]
Sedan görs samma sak med lösningen \( z_2 = -3 \). Insatt i substitutionen \( z = x^2 \) ger den:
- \[ \displaystyle z = x^2 = -3 \]
Men ekvationen \( x^2 = -3 \) har inga lösningar pga att roten \( \sqrt{-3} \) ur ett negativt tal inte är definierad.
Slutligen kan vi sammanfatta och konstatera att vår 4:e gradsekvation
- \[ x^4 - 6\,x^2 - 27 = 0 \]
har de två lösningarna:
- \[\begin{align} x_1 & = 3 \\ x_2 & = - 3 \\ \end{align}\]
En prövning bekräftar detta resultat.
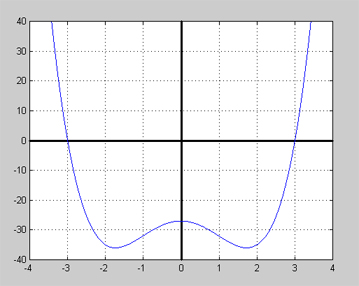
Så här ser grafen till funktionen \( y = x^4 - 6\,x^2 - 27 \) ut vars nollställen överensstämmer med våra lösningar: