1.5 Fördjupning till Kontinuerliga och diskreta funktioner
| << Förra demoavsnitt | Genomgång | Övningar | Fördjupning | Nästa demoavsnitt >> |
I genomgången sades att kontinuerlig betydde sammanhängande.
Som exempel på en kontinuerlig funktion ritades grafen till en linjär funktion med en sammanhängande rät linje. Kontinuerliga funktioners grafer kan man rita utan att lyfta pennan. Allt detta är fortfarande sant, men sådana resonemang är intuitiva.
Här följer en mer exakt matematisk definition för när en funktion är kontinuerlig och när den är diskontinuerlig:
Allmän definition för kontinuerliga funktioner
En funktion \( \, y = f(x) \, \) är kontinuerlig för \( {\color{Red} {x = a}} \) om den är definierad för \( \, x = a \, \) och om:
- \[ f(x) \to f(a) \quad {\rm när} \quad x \to a \]
Om däremot \( \, f(x) \, \) är definierad för \( \, x = a \, \), men \( f(x) \) inte \( \to f(a) \; {\rm när} \; x \to a \)
är funktionen diskontinuerlig i \( \, x = a \).
Läs den tredje raden i definitionen så här: \( \; {\rm " }f(x) \, \) går mot \( f(a)\, \) när \( x\, \) går mot \( a \, {\rm "} \).
Observera att definitionen är punktvis, dvs den talar om när en funktion är kontinuerlig för ett visst \( {\color{Red} x}\, \)-värde nämligen för \( {\color{Red} {x = a}}\, \).
Man skulle kunna lägga till att en funktion i sin helhet är kontinuerlig om den är kontinuerlig för alla \( \, x\, \). Då måste även kontinuitet prövas för varje \( \, x\, \).
Exempel 1
Låt oss titta på följande rationell funktion:
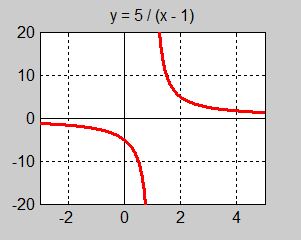
a) Är denna funktion kontinuerlig för \( {\color{Red} {x = 1}} \, \) enligt definitionen ovan?
Vi ersätter \( \, {\color{Red} a} \, \) med \( \, {\color{Red} 1} \) i definitionen. Där stär: "... om den (funktionen) är definierad för \( \, x = a \, \) OCH ... ."
Men \( f(x) \, = \, \displaystyle{5 \over x \, - \, 1}\) är inte definierad för \( {\color{Red} {x = 1}} \, \). Därför kan den inte heller vara kontinuerlig för \( {\color{Red} {x = 1}} \, \).
b) Är samma funktion kontinuerlig för \( {\color{Red} {x = 2}} \, \) enligt definitionen ovan?
I definitionen ersätter vi \( \, {\color{Red} a} \, \) med \( \, {\color{Red} 2} \) och \( \, f(x) \, \) med \( \displaystyle{5 \over x \, - \, 1}\).
Definitionen säger: \( \, f(x) = \displaystyle{5 \over x \, - \, 1} \, \) är kontinuerlig för \( \, {\color{Red} {x = 2}}\, \) om \( \, \displaystyle{5 \over x \, - \, 1} \to f(2) = \displaystyle{5 \over 2 \, - \, 1} = 5 \quad {\rm när} \quad x \to 2 \).
Vi kontrollerar detta i funktionsuttrycket: Låter vi \( \, x \, \) gå mot \( \, 2 \, \), går \( \, y \, \) mot värdet \( \, 5 \), och slutligen är \( \, f(2) = 5 \).
Detta visar också att \( \, f(x) = \displaystyle{5 \over x \, - \, 1} \) är definierad för \( \, x = 2\, \). Därmed är kontinuitetens krav uppfyllt.
Slutsats: Funktionen \( \, y = \displaystyle{5 \over x \, - \, 1} \, \) är kontinuerlig för \( \, x = 2\, \).
På samma sätt kan man undersöka om funktionen är kontinuerlig för andra \( \, x \). Sammanfattningsvis blir resultatet:
Grafen visar samma resultat: Endast i \( \, x \, = \, 1 \, \) där funktionen inte är deifinierad, skenar kurvorna iväg mot oändligheten, den ena mot \( \, + \infty\, \), den andra mot \( \, - \infty\, \). I funktionens definitionsområde (alla \( \, x \, \neq \, 1 \, \)) är kurvan sammanhängande.
Exempel 2 Teckenfunktionen
Även kallad Signumfunktionen som är definierad för alla reela tal \( \, x \, \):
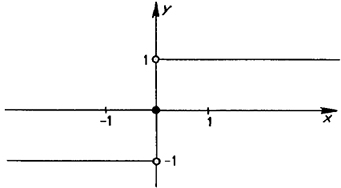
De ihåliga ringarna i grafen vid \( \, y = 1 \, \) och \( \, y = -1 \, \) betyder att dessa värden inte tillhör funktionens värdemängd, dvs \( \, sgn(0) \, \neq \, 1 \, \) och \( \, sgn(0) \, \neq \, -1 \).
Den ifyllda ringen vid origo innebär att detta värde tillhör värdemängden, dvs \( \, sgn(0) \, = \, 0 \).
Precis som hos Fibonaccis funktion är en och samma funktion definierad med olika funktionsuttryck i olika delar av dess definitionsmängd.
Kanske kan formeln ovan samt grafen, inkl. de ihåliga och ifyllda ringarna, förstås bättre med följande förenkling (OBS! Matematiskt inte korrekt):
- \[\begin{array}{rcl} sgn(\mbox{negativa}\; x) & = & -1 \\ sgn(0) & = & 0 \\ sgn(\mbox{positiva}\; x) & = & 1 \end{array}\]
Dvs \( \, sgn(x) \, \) har för negativa \( \, x \, \) värdet \( \, -1 \, \), för \( \, x = 0 \, \) värdet \( \, 0 \, \) och för positiva \( \, x \, \) värdet \( \, 1 \, \).
Låt oss nu med hjälp av den allmänna definitionen för kontinuerliga funktioner undersöka om Signumfunktionen är kontinuerlig för \( \, {\color{Red} {x = 0}} \).
Enligt definitionen borde då \( \; sgn(x) \to sgn(0) \quad {\rm när} \quad x \to 0 \).
Närmar man sig \( \, 0 \, \) på \( \, x\)-axeln från höger närmar sig \( \, sgn(x) \, \) värdet \( \, 1 \).
Närmar man sig \( \, 0 \, \) från vänster närmar sig \( \, sgn(x) \, \) värdet \( \, -1 \).
Dvs \( \, sgn(x) \to 1 \, \) och \( \to -1\, \) när \( \, x \to 0 \).
Men \( \, sgn(0) = 0 \, \). \( \, sgn(x) \, \) går dock inte mot \( \, sgn(0) = 0 \, \) när \( \, x \to 0 \), vilket den borde göra om den hade varit kontinuerlig för \( \, x = 0 \).
Därmed är kontinuitetens krav inte uppfyllt. Funktionen \( \, sgn(x) \, \) är inte kontinuerlig för \( \, x = 0 \).
Undersökar man vidare kontinuiteten för andra \( x\, \) kommer det att visa sig att \( sgn(x)\, \) är kontinuerlig för alla andra \( x\, \):
Den är kontinuerlig för alla \( \, x \neq 0 \).
I sin helhet är Signumfunktionen \( \, sgn(x) \, \) diskontinuerlig, eftersom den är diskontinuerlig i sitt definitionsområde. Diskontinuiteten i \( \, x=0 \, \) tillhör nämligen funktionens definitionsområde.
Grafen visar samma resultat: Endast i \( \, x=0 \, \) har den ett hopp, annars är grafen sammanhängande.
Olika typer av diskontinuitet
Jämför man Exempel 1 med Exempel 2 kan man konstatera: Båda funktionerna är kontinuerliga för alla \( \, x \, \) förutom för en isolerad punkt. Men funktionernas definition \(-\) och även graferna \(-\) visar ändå en ganska markant skillnad. Faktiskt handlar det om två helt olika typer av diskontinuitet i de isolerade punkterna:
Diskontinuitet av typ oändlighetsställe
I Exempel 1 är funktionen inte kontinuerlig för \( \, x = 1 \, \) därför att \( \, \displaystyle{y = {5 \over x \, - \, 1}} \, \) överhuvudtaget inte är definierad för \( x = 1\, \). Kurvorna skenar iväg mot oändligheten, den ena mot \( \, + \infty \, \), den andra mot \( \, - \infty \). Detta beror förstås på funktionsuttrycket som inte är definierad för \( \, x = 1 \). Vi har ett slags oändlighetsställe i \( x = 1\, \) vilket är ganska typiskt för rationella funktioner. Den här typen av diskontinuitet är en konsekvens av funktionens icke-definierbarhet i \( \, x = 1\, \). Annars är funktionen kontinuerlig i sin definitionsmängd.
Diskontinuitet av typ hopp
I Exempel 2 är Signumfunktionen inte kontinuerlig för \( \, x = 0\, \) därför att \( \, sgn(x) \, \) har ett hopp i sitt förlopp just i \( \, x = 0 \). Den har ett väl definierat värde för \( \, x = 0 \), nämligen \( \, sgn(0) = 0 \). Men hoppet från \( \, -1 \, \) till \( \, 0 \, \) och vidare från \( \, 0 \, \) till \( \, 1 \, \) gör att det uppstår en diskontinuitet just där. Att denna diskontinuitet är av en annan typ än oändlighetsstället i Exempel 1 är uppenbart. Till skillnad från Exempel 1 är funktionen i alla fall beräknebar, trots diskontinuiteten. Ja, den är t.o.m en bra modell för verkligheten, för så beter sig en signal när den hoppar från noll till ett, nämligen diskontinuerligt.
Det finns även andra typer av diskontinuitet, men oändlighetsställe och hopp är de oftast förekommande hos kontinuerliga funktioner.
Copyright © 2011-2018 Math Online Sweden AB. All Rights Reserved.