1.1 Fördjupning till Polynom

Fördjupning

Polynomfunktioner av högre grad

När ett polynom tilldelas en annan variabel, säg \( \, y \, \) bildas en polynomfunktion. I Matte 1-kursen hade vi bara linjära eller 1:a gradsfunktioner av typ:

\[ y = 4\,x + 12 \]

Till höger om likhetstecknet står ett polynom där \( \, x \, \) förekommer som 1:a gradspotens dvs med exponenten \( \, 1 \, \). Därför kallas \( \, 4\,x \, \) polynomets linjära term. Polynomets konstanta term är \( \, 12 \). Grafen till denna 1:a gradsfunktion är en rät linje. I Matte 2-kursen gick vi ett steg vidare och sysslade med 2:a gradsfunktioner av typ:

\[ y = 3\,x^2 + 5\,x - 16 \]

Här är graden \( \, 2 \). Den kvadratiska termen är \( \, 3\,x^2 \, \), den linjära termen \( \, 5\,x\, \) och den konstanta termen \( \, -16 \). Grafen till denna 2:a gradfunktion är en parabel. Dessa funktioner kallas polynomfunktioner därför att uttrycken till höger om likhetstecken är polynom, dvs summor av termer där exponenterna till \( \, x\)-potenserna är positiva heltal eller \( \, 0 \). I Matte 3-kursen ska vi nu lära oss att hantera även polynom av högre grad än \( \, 2 \).

Exempel på polynomfunktion av högre grad

Vi tar som exempel följande 4:e gradspolynomfunktion:

\[ y = x^4 - 29\;x^2 + 100 \]

vars graf till höger är mer komplicerad än en parabel.

Den har framför allt fler minima, maxima och nollställen.

Funktionens fyra nollställen är identiska med lösningarna till 4:e gradsekvationen:

\[ x^4 - 29\;x^2 + 100 = 0 \]

En familj av högre grads polynomfunktioner

Ett polynoms grad är ett mått på dess komplexitet: Ju högre grad, desto oftare svänger kurvorna och desto fler maxima/minima har de. Här ser man sex polynom vars grafer är ritade i samma koordinatsystem:

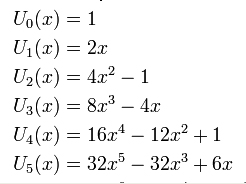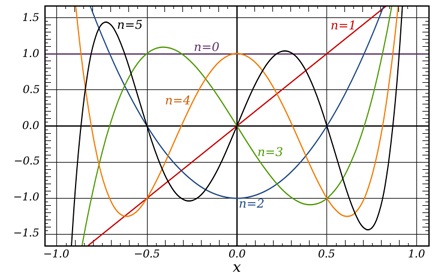Polynom av \( n\)-te grad har \( n-1 \) svängningar (maxima/minima):

\( U_5(x) \) (svart kurva) är av \( 5\):e grad och har \( 4 \) svängningar (maxima/minima).

\( U_4(x) \) (gul kurva) är av \( 4\):e grad och har \( 3 \) svängningar (maxima/minima).

\( U_3(x) \) (grön kurva) är av \( 3\):e grad och har \( 2 \) svängningar (maxima/minima).

\( U_2(x) \) (blå kurva) är av \( 2\):a grad och har \( 1 \) svängning (maxima/minima).

Dessa polynom kallas för Chebyshevpolynom efter den ryske matematikern Chebyshev som definierade dem 1854 med följande s.k.

Rekursionsformel

\( U_n(x) = 2\,x\,\cdot\,U_{n-1}(x)\,-\,U_{n-2}(x) \qquad\qquad n = 2, 3, ... \)

\( U_0(x) = 1, \quad U_1(x) = 2\,x \)

Användning av rekursionsformeln

Ställ upp de Chebyshevpolynomen \( \, U_2, \, U_3, \, U_4\,\) med hjälp av de två första \( \, U_0, \, U_1 \).

\[ \displaystyle U_0(x) = \underline{1} \]

\[ U_1(x) = \underline{2\,x} \]

För \(n = 2\,\) ger rekursionsformeln:

\[ U_2(x) = 2\,x\,\cdot\,U_1(x)\,-\,U_0(x) = 2\,x\,\cdot\,2\,x\,-\,1 = \underline{4\,x^2\,-\,1} \]

Sedan kan vi få fram \( U_3(x) \) genom att att sätta in n = 3 i rekursionsformeln:

\[ U_3(x) = 2\,x\,\cdot\;U_2(x)\,-\,U_1(x) = 2\,x\,\cdot\,(4\,x^2\,-\,1)\,-\,2\,x = 8\,x^3\,-\,2\,x\,-\,2\,x = \underline{8\,x^3\,-\,4\,x} \]

För \(n = 4\,\) ger rekursionsformeln \( U_4(x) \) osv.:

\[ U_4(x) = 2\,x\,\cdot\,U_3(x)\,-\,U_2(x) = 2\,x\,\cdot\,(8\,x^3\,-\,4\,x)\,-\,(4\,x^2\,-\,1) = 16\,x^4\,-\,8\,x^2\,-\,4\,x^2\,+\,1 = \underline{16\,x^4\,-\,12\,x^2\,+\,1} \]

De nedsänkta indexen \(_0,\,_1,\,_2,\,_3,\,_4,\,_5\) i beteckningarna \(U_0, U_1, U_2, U_3, U_4, U_5\,\) används både för att relatera indexet till polynomets grad och kunna definiera dem med rekursionsformeln.

Rekursion är ett koncept som används för att få fram resultat genom successiv upprepning av beräkningar.

Rekursionsformeln ger oss möjligheten att ställa upp ett Chebyshevpolynom med hjälp av de två föregående. De första två Chebyshevpolynomen \( \, U_0, \, U_1 \, \) är explicit angivna i rekursionsformelns andra rad. Det tredje Chebyshevpolynomet \(U_2\,\) får man genom att sätta in \( \, U_0, \, U_1 \,\) i rekursionsformelns högerled. Det fjärde Chebyshevpolynomet \( \, U_3 \, \) får man genom att sätta in \( \, U_1, \, U_2 \, \) i högerledet. \(U_4\,\) får man genom att sätta in \( \, U_2, \, U_3 \,\) i högerledet osv.

Jämförelse av koefficienter

Jämförelse av koefficienter är en teknik eller en metod som vi kommer att använda för att lösa högre gradsekvationer genom att faktorisera polynom av högre grad än 2, se övningarna 10-12. Metoden bygger på begreppet likhet mellan polynom.

Definition: \( \quad \) Två polynom

\[ \; P(x) = a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad \ldots \quad + a_1 \cdot x + a_0 \]

\[ \; Q(x) = b_n \cdot x^n + b_{n-1} \cdot x^{n-1} + \quad \ldots \quad + b_1 \cdot x + b_0 \]

är lika med varandra om de har samma grad och om alla deras motsvarande koefficienter, dvs om:

\[ \; a_n = b_n, \qquad a_{n-1} = b_{n-1}, \qquad \ldots \qquad a_1 = b_1, \qquad a_0 = b_0 \]

Exempel 1

Följande två polynom är givna där \( a\, \) och \( b\, \) är konstanter medan \( x\, \) är polynomens oberoende variabel:

\[ P(x) = a \cdot x + 2\,a + b \]

\[ Q(x) = 2\,x + 1\!\, \]

För vilka värden på \( a\, \) och \( b\, \) är de två polynomen lika med varandra?

Lösning:

Vi skriver \( P(x),\, \) och \( Q(x)\, \) så att vi lättare kan se motsvarande koefficienter:

\[ P(x) = a \cdot x^1 + (2\,a + b) \cdot x^0 \]

\[ Q(x) = 2 \cdot x^1 + \quad\;\; 1 \quad\;\; \cdot x^0 \]

Jämförelse av koefficienterna till \( x^1\, \) leder till:

\[ a = 2\,\]

Jämförelse av koefficienterna till \( x^0 \,\) leder till:

\[ 2\,a + b = 1\!\,\]

Sätter man in \( a = 2\, \) i denna relation får man \( b = -3\, \).

Polynomen \( P(x)\, \) och \( Q(x)\, \) är lika med varandra för:

\[ a = 2\, \]

\[ b = -3\, \]

Exempel 2 Polynomdivision

Utför polynomdivisionen: \( \qquad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2) \)

En annan formulering av uppgiften är:

Hitta ett 2:a gradspolynom \( \, Q(x)\, \) så att \( \, Q(x)\cdot (x-2) = P(x) \),

där \( \, P(x) = x^3 + 4\,x^2 + x - 26 \).

Lösning:

Det 2:a gradspolynomet \( Q(x)\, \) kan skrivas så här:

\[ Q(x) = a\,x^2 + b\,x + c \]

Vi bestämmer koefficienterna \( a\, , \, b\, \) och \( c\, \) så att \( {\color{White} x} Q(x)\cdot (x-2) \, = \, P(x) \):

\[\begin{array}{rclc} Q(x) \cdot (x - 2) & = & (a\,x^2 + b\,x + c)\cdot (x - 2) & = \\ & = & a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c & = \\ & = & a\,x^3 + (-2\,a + b)\,x^2 + (-2\,b + c)\,x - 2\,c & = \\ & = & a \cdot x^3 + (-2\,a + b) \cdot x^2 + (-2\,b + c) \cdot x - 2\,c \cdot x^0 & \\ P(x) & = & 1 \cdot x^3 + \quad\;\;\;\;4 \quad\;\; \cdot x^2 + \quad\;\;\;\,1 \quad\;\; \cdot x - 26 \cdot x^0 \end{array} \]

Jämförelse av koefficienterna till \( x^3 \)-termen ger:

\[ a = 1 \]

Jämförelse av koefficienterna till \( x^2 \)-termen ger:

\[\begin{align} -2\,a + b & = 4 \\ -2\cdot 1 + b & = 4 \\ - 2 + b & = 4 \\ b & = 6 \\ \end{align} \]

Jämförelse av koefficienterna till \( x^1 \)-termen ger:

\[\begin{align} -2\,b + c & = 1 \\ -2\cdot 6 + c & = 1 \\ -12 + c & = 1 \\ c & = 13 \\ \end{align} \]

Jämförelse av koefficienterna till \( x^0 \, \)-termen bekräftar värdet på \( c \, \):

\[\begin{align} - 2\,c & = - 26 \\ c & = 13 \\ \end{align} \]

Vi får \( a = 1\, , \, b = 6\, \) och \( c = 13\, \) och därmed: \( \quad Q(x) = x^2 + 6 \, x + 13 \)

Alltså är: \( \qquad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2) \; = \; x^2 + 6 \, x + 13\)

Anmärkningar

Vanligtvis behandlar man polynomdivision genom att direkt dividera polynom med varandra. Man använder olika speciella uppställningstekniker, vilket inte besvarar frågan vilket man ska välja. Jämförelse av koefficienter löser polynomdivision på ett generellt sätt, eftersom den är en generell metod inte bara för faktorisering av polynom utan även för andra problem där ett polynom är efterfrågad. Dessutom får man mer insikt i polynomens struktur.

I litteraturen förekommer även ett annat namn för den metod som beskrevs ovan. Istället för jämförelse av koefficienter som vi använder pratar man om metoden med obestämda koefficienter (eng.: the method of undetermined coefficients). Med obestämda koefficienter menar man den ansats som man i början gör med obestämda koefficienter som man sedan bestämmer under metodens gång.