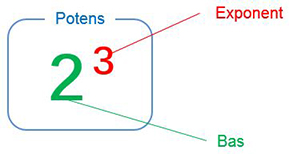
Potenser
| \( \pmb{\gets} \) Tillbaka till Polynom | Genomgång | Övningar |
Potenser är ett repeterande underavsnitt i avsnittet Polynom. Övningar till Potenser finns separat i fliken ovan.
Hur räknar du?
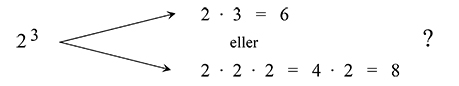 \[ {\rm {\color{Red} {OBS!\quad Vanligt\,fel:}}} \quad\; 2\,^3 \; = \; 6 \]
\[ {\rm {\color{Red} {OBS!\quad Vanligt\,fel:}}} \quad\; 2\,^3 \; = \; 6 \]
\[ \qquad\quad\;\, {\rm Rätt:} \qquad\qquad\! 2\,^3 \; = \; 2 \cdot 2 \cdot 2 \; = \; 4 \cdot 2 \; = \; 8 \]
Felet beror på att man blandar ihop två olika räkneoperationer: multiplikationen med upphöjt till.
I själva verket betyder \( \, 2\,^{\color{Red} 3} \, \) inte \( \, 2 \cdot 3 \, \) utan \( \, \underbrace{2 \cdot 2 \cdot 2}_{{\color{Red} 3}\;\times} \, \) som sedan förkortas till \( \, 2\,^{\color{Red} 3} \).
Vad är en potens?
\( \, 2\,^3 \, \) läses \( \, {\color{Red} 2} \) upphöjt till\( \, {\color{Red} 3} \, \) och kallas för potens. \( \, 2\, \) heter basen och \( \, 3 \, \) exponenten.
Exponenten \( \, {\color{Red} 3} \, \) är inget tal som ingår i beräkningen, utan endast en information om att \( \, 2 \, \) ska multipliceras \( \, {\color{Red} 3} \, \) gånger med sig själv (jfr. upprepad addition).
Därför det är fel att multiplicera \( \, 2 \, \) med \( \, {\color{Red} 3} \, \) när man ska beräkna \( \, 2\,^{\color{Red} 3} \).
Exempel
Förenkla: \( \qquad \displaystyle{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \)
Lösning: \( \qquad \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \over 2 \cdot 2 \cdot 2 \cdot 2} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot \cancel{2 \cdot 2 \cdot 2 \cdot 2} \over \cancel{2 \cdot 2 \cdot 2 \cdot 2}} \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} \)
- OBS! Förenkla alltid först, räkna sedan!
Snabbare: \( \qquad\!\! \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, 2\,^{3\,+\,5\,-\,4} \, = \, 2\,^4 \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} \)
För att förstå den snabbare lösningen måste man känna till:
Potenslagarna
Följande lagar gäller för potenser där basernna \( \, a,\,b \, \) är tal \( \, \neq 0 \, \) och exponenterna \( \, x,\,y \, \) är godtyckliga tal:
Första potenslagen: \( \qquad\qquad\quad\;\, a^x \cdot a^y \; = \; a\,^{x \, + \, y} \qquad\qquad \)
Andra potenslagen: \( \qquad\qquad\qquad\;\;\; \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \qquad\qquad \)
Tredje potenslagen: \( \qquad\qquad\qquad \displaystyle {(a^x)^y} \; = \; a\,^{x \, \cdot \, y} \qquad\qquad \)
Lagen om nollte potens: \( \qquad\qquad\quad\;\;\, a\,^0 \; = \; 1 \qquad\qquad \)
Lagen om negativ exponent: \( \qquad\quad\;\;\; a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad\qquad \)
Potens av en produkt: \( \qquad\qquad\;\, (a \cdot b)\,^x \; = \; a\,^x \cdot b\,^x \qquad\qquad \)
Potens av en kvot: \( \qquad\qquad\qquad\, \left(\displaystyle {a \over b}\right)^x \; = \; \displaystyle {a\,^x \over b\,^x} \qquad\qquad \)
Potenser med positiva exponenter
Potensen \( \, a\,^{\color{Red} x} \, \) med positiv exponent (\( x \, \) heltal \( > 0 \, \) och \( \, a \, \neq 0 \)) kan definieras som:
- Upprepad multiplikation av \( \, a \, \) med sig själv, \( \, {\color{Red} x} \, \) gånger:
- \( \quad a\,^{\color{Red} x} = \underbrace{a \cdot a \cdot a \cdot \quad \ \cdots \quad \cdot a}_{{\color{Red} x}\;{\rm gånger}} \)
Exempel på första potenslagen
Förenkla: \( \quad\;\; a\,^2 \, \cdot \, a\,^3 \)
Lösning:
- \( a\,^2 \cdot a\,^3 \; = \; \underbrace{a \cdot a}_{2\;\times} \; \cdot \; \underbrace{a \cdot a \cdot a}_{3\;\times} \; = \; \underbrace{a \cdot a \cdot a \cdot a \cdot a}_{{\color{Red} 5}\;\times} \; = \; a\,^{\color{Red} 5}\)
Snabbare:
- \( a\,^2 \cdot a\,^3 \; = \; a\,^{2\,+\,3} = \; a\,^{\color{Red} 5} \)
Den snabbare lösningen ovan är ett exempel på den första potenslagen. Nedan följer ett exempel på den andra potenslagen.
Exempel på andra potenslagen
- \( \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; {a \cdot a \cdot a \cdot a \cdot a \; \over \; a \cdot a \cdot a} \; = \; {a \cdot a \cdot \cancel{a \cdot a \cdot a} \; \over \; \cancel{a \cdot a \cdot a}} \; = \; a \cdot a \; = \; a\,^2 \)
Snabbare:
- \( \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; a\,^{{\color{Red} {5\,-\,3}}} \; = \; a\,^2 \)
Potensbegreppet definierades inledningsvis endast för positiva exponenter. Men den definitionen duger inte för negativa exponenter.
Antalet multiplikationer av basen med sig själv kan inte vara negativt. Det behövs en ny definition.
Potenser med negativa exponenter
Exempel på potens med negativ exponent:
- \[ \;\; \displaystyle 2\,^{\color{Red} {-3}} \; = \;\; 1\,/\,\underbrace{2 \, / \, 2 \, / \, 2}_{{\color{Red} 3}\;\times} \; = \; 1 \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \; = \; \frac{1}{\underbrace{2 \, \cdot \, 2 \, \cdot \, 2}_{{\color{Red} 3}\;\times}} \; = \; \frac{1}{2\,^{\color{Red} {3}}} \; = \; \frac{1}{8} \quad \]
Potens med negativ exponent = upprepad division av \( \, 1 \, \) med basen \( \, 2 \), \( \, {\color{Red} 3} \, \) gånger.
Eller: \( \qquad\qquad\qquad\qquad\qquad\; \) upprepad multiplikation med basens invers \( \displaystyle \frac{1}{2} \), \( \, {\color{Red} 3} \, \) gånger.
Negativ exponent innebär att invertera potensen med positiv exponent.
Andra exempel: \( \qquad\qquad\qquad \) Att "invertera" t.ex. \( \, 10 \, \) ger \( \, \displaystyle {1 \over 10} \)
- \[ \displaystyle{10\,^{-1} \, = \, {1 \over 10\,^1} \, = \, {1 \over 10} \, = \, 0,1} \]
- \[ \displaystyle{10\,^{-2} \, = \, {1 \over 10\,^2} \, = \, {1 \over 10 \cdot 10} \, = \, {1 \over 100} \, = \, 0,01} \]
- \[ \displaystyle{10\,^{-3} \, = \, {1 \over 10\,^3} \, = \, {1 \over 10 \cdot 10 \cdot 10} \, = \, {1 \over 1000} \, = \, 0,001} \]
Generellt:
Potensen \( \, a\,^{\color{Red} {-x}} \, \) med negativ exponent (\( x \, \) heltal \( > 0 \, \) och \( \, a \, \neq 0 \)) kan definieras som:
- Upprepad division av \( \, 1 \, \) med basen \( \, a \, \) (eller multiplikation med \( \, \displaystyle \frac{1}{a} \, \)), \( \, {\color{Red} x} \, \) gånger:
- \( \displaystyle a\,^{\color{Red} {-x}} \; = \; 1 \, / \, \underbrace{a \, / \, a \, / \, a \, / \quad \ \cdots \quad / a}_{{\color{Red} x}\;{\rm gånger}} \quad {\color{Red} =} \quad 1 \cdot \underbrace{\frac{1}{a} \cdot \frac{1}{a} \cdot \frac{1}{a} \cdot \quad \cdot \cdots \quad \cdot \frac{1}{a}}_{{\color{Red} x}\;{\rm gånger}} \; = \; {1 \over a^x}\)
Övergången från division till multiplikation (den röda likheten) kan motiveras så här:
Uppfattar man \( \, a \, \) som ett bråk med nämnaren \( \, 1 \, \) dvs \( \, \displaystyle \frac{a}{1} \), kan man ersätta divisionerna med multiplikationer med det inversa \( \, \displaystyle \frac{1}{a} \).
I Bråkräkning hade vi lärt oss att division med ett bråk kan skrivas som en multiplikation med det inversa bråket.
Bevis av två potenslagar
Påstående:
Lagen om negativ exponent \( \quad a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \; \)
Bevis:
- \( \displaystyle{1 \over a^x} \; = \; \displaystyle{a^0 \over a^x} \; = \; a^{0-x} \; = \; a^{-x} \)
In den första likheten har vi använt lagen om nollte potens baklänges: \( \; 1 = a^0 \; \).
In den andra likheten har vi använt andra potenslagen: \( \; \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \; \).
Efter dessa steg får vi påståendet, fast baklänges.
Potenser med \( \, 0 \, \) i exponenten
Påstående:
Lagen om nollte potens \( \quad a^0 \; = \; 1 \; \)
Bevis:
Påståendet kan bevisas genom att använda andra potenslagen:
- \( \displaystyle{a^x \over a^x} \; = \; a^{x-x} \; = \; a^0 \)
Å andra sidan vet vi att ett bråk med samma täljare som nämnare har värdet \( \, 1 \):
- \( \displaystyle{a^x \over a^x} \; = \; 1 \)
Av raderna ovan följer påståendet:
- \( a^0 \; = \; 1 \)
Exemplet nedan illustrerar lagen ovan genom att visa att potenser med negativa exponenter är en naturlig fortsättning på potenser med positiva exponenter och nollte potensen däremellan (Potens \( \; = \; \) upprepad multiplikation):
Varför är \( \; 5\,^0 \, = \, 1 \; \)?
- \[ \;\; 5^4 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \cdot 5 \]
- \[ \;\; 5^3 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \]
- \[ \;\; 5^2 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \]
- \[ \;\; 5^1 \; = \; {\color{Red} 1} \cdot 5 \]
- \[ \; \boxed{{\color{Red} {5^0 \; = \; 1}}} \]
- \[ \;\; 5^{-1} \; = \; \displaystyle{{\color{Red} 1} \over 5} \]
- \[ \;\; 5^{-2} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5} \]
- \[ \;\; 5^{-3} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5} \]
- \[ \;\; 5^{-4} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5 \cdot 5 } \]
Att \( \; {\color{Red} 1} \)-orna följer med hela tiden beror på att multiplikationens enhet är \( \, {\color{Red} 1} \), dvs \( \, a \cdot {\color{Red} 1} \, = \, a \).
Därför blir endast \( \, {\color{Red} 1} \, \) kvar, när vi kommer till \( \, {\color{Red} {5^0}} \, \) då alla \( \, 5\)-or har försvunnit.
Jämför med produkter med negativa faktorer som är en naturlig fortsättning på produkter med positiva faktorer och nollprodukten däremellan (Produkt \( \; = \; \) upprepad addition: \( \, {\color{Red} 0} \, \) tar över rollen av \( \, {\color{Red} 1} \)):
Varför är \( \; 5 \cdot 0 \, = \, 0 \; \)?
- \[ \;\; 5 \cdot 4 \; = \; {\color{Red} 0} + 5 + 5 + 5 + 5 \]
- \[ \;\; 5 \cdot 3 \; = \; {\color{Red} 0} + 5 + 5 + 5 \]
- \[ \;\; 5 \cdot 2 \; = \; {\color{Red} 0} + 5 + 5 \]
- \[ \;\; 5 \cdot 1 \; = \; {\color{Red} 0} + 5 \]
- \[ \; \boxed{{\color{Red} {5 \cdot 0 \; = \; 0}}} \]
- \[ \;\; 5 \cdot (-1) \; = \; {\color{Red} 0} - 5 \]
- \[ \;\; 5 \cdot (-2) \; = \; {\color{Red} 0} - 5 - 5 \]
- \[ \;\; 5 \cdot (-3) \; = \; {\color{Red} 0} - 5 - 5 - 5 \]
- \[ \;\; 5 \cdot (-4) \; = \; {\color{Red} 0} - 5 - 5 - 5 - 5 \]
Att \( \; {\color{Red} 0} \)-orna följer med hela tiden beror på att additionens enhet är \( \, {\color{Red} 0} \), dvs \( \, a + {\color{Red} 0} \, = \, a \).
Därför blir endast \( \, {\color{Red} 0} \, \) kvar, när vi kommer till \( \, {\color{Red} {5 \cdot 0}} \, \) då alla \( \, 5\)-or har försvunnit.
Potenser med rationella exponenter
Potenser med exponenter som är rationella tal (bråktal) kan användas för att beräkna (högre) rötter.
Påstående (högre rötter):
- \( a^{1 \over n} \; = \; \sqrt[n]{a} \; \) \( , \qquad n\neq 0 \)
Bevisidé:
Vi tar specialfallet \( n=3 \), multiplicerar \( a \)\(^{1 \over 3} \) tre gånger med sig själv och använder potenslagen om produkt av potenser med samma bas:
- \( \displaystyle a^{1 \over 3} \cdot a^{1 \over 3} \cdot a^{1 \over 3} \; = \; a^{{1 \over 3} + {1 \over 3} + {1 \over 3}} \; = \; a^{3 \over 3} \; = \; a^1 \; = \; a \)
Definitionen för 3:e roten ur \( a \) är:
\( \qquad\quad \displaystyle \sqrt[3]{a} \; = \; \) Tal som 3 gånger multiplicerat med sig själv ger \( a \).
Men enligt ovan är det tal som 3 gånger med sig själv ger \( a \), just \( a \) \(^{1 \over 3} \). Alltså måste detta tal vara lika med 3:e roten ur \( a \):
- \( \displaystyle a^{1 \over 3} \; = \; \sqrt[3]{a} \)
Denna bevisidé kan vidareutvecklas till det allmänna fallet för alla heltal \( m\, \) och \( n\neq 0 \, \) (Lagen om rationell exponent):
- \( a^{m \over n} \; = \; \sqrt[n]{a^m} \)
Potensekvationer
Anta i fortsättningen att \( \, x \, \) är en okänd variabel och \( b\, \) och \( c\, \) givna konstanter \( \neq 0 \) .
- Funktioner av typ \( y = x^3\, \) kallas potensfunktioner, generellt \( \; y = c \cdot x^b\, \).
- Ekvationer av typ \( x^3\, = 8 \) kallas potensekvationer, generellt \( \; x^b\, = c \).
I potensfunktioner och -ekvationer förekommer \( \, x \, \) i basen. Potensekvationer löses genom rotdragning. För t.ex. potensekvationen \( x^3\, = 8 \) finns det två olika sätt att beskriva lösningen via rotdragning:
- \[\begin{align} x^3 & = 8 \qquad & | \; \sqrt[3]{\;\;} \\ \sqrt[3]{x^3} & = \sqrt[3]{8} \\ x & = 2 \\ \end{align}\]
Alternativt (med rationell exponent):
- \[\begin{align} x^3 & = 8 \qquad & | \; (\;\;\;)^{1 \over 3} \; \text{samma som} \; \sqrt[3]{\;\;} \\ (x^3)^{1 \over 3} & = 8^{1 \over 3} \\ x^{3\cdot{1 \over 3}} & = 8^{1 \over 3} \\ x & = 2 \\ \end{align}\]
Det alternativa sättet att lösa ekvationen ovan visar att rötter även kan uppfattas och skrivas som potenser med rationella exponenter.
Blandade exempel
Potenser med rationella exponenter
Potenser med exponenter som är rationella tal (bråktal) kan användas för att beräkna (högre) rötter.
Påstående (högre rötter):
- \( a^{1 \over n} \; = \; \sqrt[n]{a} \; \) \( , \qquad n\neq 0 \)
Bevisidé:
Vi tar specialfallet \( n=3 \), multiplicerar \( a \)\(^{1 \over 3} \) tre gånger med sig själv och använder potenslagen om produkt av potenser med samma bas:
- \( \displaystyle a^{1 \over 3} \cdot a^{1 \over 3} \cdot a^{1 \over 3} \; = \; a^{{1 \over 3} + {1 \over 3} + {1 \over 3}} \; = \; a^{3 \over 3} \; = \; a^1 \; = \; a \)
Definitionen för 3:e roten ur \( a \) är:
\( \qquad\quad \displaystyle \sqrt[3]{a} \; = \; \) Tal som 3 gånger multiplicerat med sig själv ger \( a \).
Men enligt ovan är det tal som 3 gånger med sig själv ger \( a \), just \( a \) \(^{1 \over 3} \). Alltså måste detta tal vara lika med 3:e roten ur \( a \):
- \( \displaystyle a^{1 \over 3} \; = \; \sqrt[3]{a} \)
Denna bevisidé kan vidareutvecklas till det allmänna fallet för alla heltal \( m\, \) och \( n\neq 0 \, \) (Lagen om rationell exponent):
- \( a^{m \over n} \; = \; \sqrt[n]{a^m} \)
Potensekvationer
Anta i fortsättningen att \( \, x \, \) är en okänd variabel och \( b\, \) och \( c\, \) givna konstanter \( \neq 0 \) .
- Funktioner av typ \( y = x^3\, \) kallas potensfunktioner, generellt \( \; y = c \cdot x^b\, \).
- Ekvationer av typ \( x^3\, = 8 \) kallas potensekvationer, generellt \( \; x^b\, = c \).
I potensfunktioner och -ekvationer förekommer \( \, x \, \) i basen. Potensekvationer löses genom rotdragning. För t.ex. potensekvationen \( x^3\, = 8 \) finns det två olika sätt att beskriva lösningen via rotdragning:
- \[\begin{align} x^3 & = 8 \qquad & | \; \sqrt[3]{\;\;} \\ \sqrt[3]{x^3} & = \sqrt[3]{8} \\ x & = 2 \\ \end{align}\]
Alternativt (med rationell exponent):
- \[\begin{align} x^3 & = 8 \qquad & | \; (\;\;\;)^{1 \over 3} \; \text{samma som} \; \sqrt[3]{\;\;} \\ (x^3)^{1 \over 3} & = 8^{1 \over 3} \\ x^{3\cdot{1 \over 3}} & = 8^{1 \over 3} \\ x & = 2 \\ \end{align}\]
Det alternativa sättet att lösa ekvationen ovan visar att rötter även kan uppfattas och skrivas som potenser med rationella exponenter.
Internetlänkar
http://www.youtube.com/watch?v=iYgG4LUqXks
http://www.webbmatte.se/gym/arabiska/2/2_8_4sv.html
http://www.webbmatte.se/gym/arabiska/2/2_8_3sv.html
http://wiki.math.se/wikis/forberedandematte1/index.php/1.3_%C3%96vningar
Copyright © 2010-2016 Math Online Sweden AB. All Rights Reserved.