1.1 Om tal

Teori

Innehåll

1 Talbegreppet
2 Abstraktion
3 Olika typer av tal
4 Vårt talsystem
5 Exempel 1
6 Exempel 2
7 Exempel 3
8 Internetlänkar

Talbegreppet

Aritmetik \(-\) vårt första kapitel i Matte \(1\)-kursen \(-\) betyder läran om tal. Men vad är ett tal egentligen? Titta på följande exempel:

Fil:Images tre katter.jpg \(\qquad\) \(\qquad\) Fil:Images tre hundar.jpg \(\qquad\) \(\qquad\)

Självfallet är tre katter inte lika med tre hundar. Men fundera: Vad är det gemensamma hos tre katter och tre hundar? Om man bortser från själva katter och hundar så är det antalet tre som är gemensamt för båda mängder. Och just detta gemensamma kallas för talet 3. Tal kan alltså uppfattas som antalet saker och ting som finns i en mängd. Detta förutsätter att vi redan har lärt oss att räkna saker och ting \(-\) som barn. I själva verket är det en tankeprocess som ligger bakom räknandet. Men den är i regel omedveten.

Tankeprocessen består i att bortse från skillnader (katter och hundar) och att bibehålla det gemensamma (antalet tre) hos olika verkliga objekt och kallas:

Abstraktion

abstrahere betyder på latin: att ta bort, att dra av. Man tar bort det som skiljer tre katter från tre hundar och kommer till det som är som gemensamt hos dem: Antalet 3 eller enklare talet 3.

Matematik är en abstrakt vetenskap.

Redan begreppet tal är resultatet av abstraktion i den mänskliga hjärnan: Att bortse från det som skiljer och behålla det som är gemensamt. Källan är alla verkliga objekt som omger oss.

Ett växande barn lär sig denna abstraktionsförmåga under sin uppväxt. Mänskligheten har lärt sig den under den historiska utvecklingen. För oss känns det som en självklarhet att skilja mellan antalet saker och ting i en mängd och mängdens andra egenskaper. Men det finns naturfolk som t.ex. betecknar i sitt språk två kvinnor med ett annat ord än två pilar. De använder olika ord för samma antal när antalen används i kombination med olika objekt. Hos dem har antalet saker och ting i en mängd inte löst sig (inte abstraherats) från mängdens andra egenskaper.

Abstraktion är ett viktigt koncept i allt tänkande, så även i matematiken. Den ger oss inte bara talbegreppet. Man kan t.o.m. säga att hela matematiken består av en rad abstraktioner på olika nivåer. Vill man bli duktig i matte är det bäst att träna sin abstraktionsförmåga. Och hur gör man det? Bl.a. genom att just syssla med matematik!

Olika typer av tal

Allt vi sade ovan är åtminstone sant om vi nöjer oss med den enklaste typen av tal, de positiva heltalen:

dvs antalet saker och ting i en mängd \(-\) det som vi kan börja med att räkna med våra fingrar. Generellt är positiva tal alla tal större än \( \, 0 \, \). Till själva nollan kommer man genom att dra av samma tal från varandra, t.ex. \( \, 4 - 4 = 0 \, \). De positiva heltalen bildar tillsammans med \( \, 0 \, \) de s.k. naturliga talen:

Drar man av ett större naturligt tal från ett mindre, t.ex. \( 4 - 5 = -1 \), kommer man till negativa tal. De naturliga talen bildar tillsammans med de negativa talen de s.k. heltalen:

Delar man två heltal med varandra, t.ex. \( 1 / 3 = \displaystyle{1 \over 3} \), kommer man till bråktal. Heltalen bildar tillsammans med bråktalen de s.k. rationella talen:

Drar man t.ex. roten av 2 kommer man till ett s.k. irrationellt tal:

\[ \, \sqrt{2} = 1,4142135623730950488016887242097\ldots \, \]

Detta är ett irrationellt tal därför att det har oändligt många decimaler utan

något upprepande mönster. Därför kan \( \, \sqrt{2} \, \) inte längre skrivas som ett bråktal.

Rationella talen bildar tillsammans med de irrationella talen de s.k. reella talen.

Löser man t.ex. ekvationen \( x^2 + 1 = 0 \) kommer man till ett s.k. imaginärt tal:

\[ \, x = \sqrt{-1} \, \]

De reella talen bildar tillsammans med de imaginära talen de s.k. komplexa talen.

Bilden till höger visar hur de olika taltyperna är delmängder av varandra.

Alla typer av tal bygger sin konstruktion på och är resultat av abstraktioner, i princip

av samma typ som vi inledningsvis introducerade talbegreppet \(-\) fast på högre nivå.

\( \qquad \)Fil:Taltypera.jpg

Vårt talsystem

Att tänka sig ett tal eller att räkna upp antalet saker och ting i en mängd, är en sak. Att beteckna tal, meddela det till andra dvs att kommunicera tal så att alla förstår, är en helt annan sak.

Man pratar om representation av tal, dvs att visa eller framställa talet. Det har funnits genom historien en uppsjö av olika sätt att representera tal. Det sätt som idag används i kommunikation bland människor världen över \(-\) vårt talsystem idag \(-\) är det s.k. decimala positionssystemet.

Decimalt heter det därför att det bygger på basen \( \, 10 \, \) (på latin: deci). Dvs man använder de \( \, 10 \, \) siffrorna för att representera alla tal:

Antagligen har urmänniskan räknat första gången genom att räkna upp sina \( \, 10 \, \) fingrar. Det är praktiskt - och vi gör det även idag - att ta sina fingrar till hjälp när man räknar i huvudet. Allt som går över \( \, 10 \, \) bildas med hjälp av dessa 10.

Positionssystem heter vårt talsystem därför att det är positionen eller placeringen av siffrorna \( \, 0\)-\(9 \, \) i talet som bestämmer talets värde. Det som bestämmer värdet, de olika positionerna har fått beteckningarna:

ental
tiotal
hundratal
tusental
tiotusental
osv.

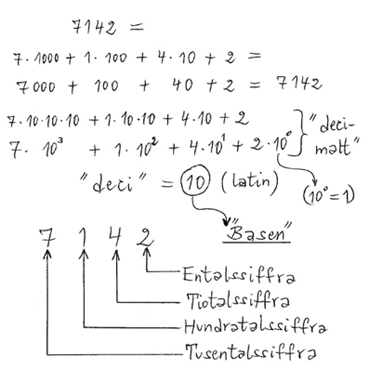
Man börjar att skriva från vänster siffran med det högsta värdet. Sedan följer de andra med nedstigande värden. Så siffran med det minsta värdet, entalet, hamnar längst till höger. T.ex. så här:

Om du har svårigheter att förstå skrivsättet med \( \, 10\)-potenser läs avsnittet om Potenser. Kom speciellt ihåg att enligt potenslagarna \( \, 10^0 \, = \, 1 \, \).

Exempel 1

I talet \( \, 312 \, \) är - om vi börjar från höger - siffran \( \, 2 \, \) pga sin position (placering) ett ental. Nästa siffra från höger, \( \, 1 \, \) är ett tiotal och siffran \( \, 3 \, \) ett hundratal. Eftersom \( \, 3 \, \) är ett hundratal har siffran \( \, 3 \, \) värdet \( \, 3 \cdot 100 \) dvs \( \, 300 \, \). Eftersom \( \, 1 \, \) är ett tiotal har siffran \( \, 1 \, \) värdet \( \, 1 \cdot 10 \, \) dvs \( \, 10 \, \). Analogt har siffran \( \, 2 \, \) värdet \( \, 2 \cdot 1 \, \) dvs \( \, 2 \, \). Summerar man alla siffrors värden beräknas talets värde till:

\[ {\color{Red} 3} \, \cdot100 + {\color{Red} 1}\cdot10 + {\color{Red} 2}\cdot1 = 300 + 10 + 2 = {\color{Red} {312}} \, \]

Man säger att \( \, 312 \, \) är ett sätt - det decimala positionssystemets sätt - att visa (att representera, att framställa) talets värde.

Om man i exemplet ovan istället för \( \, 100 \, \) skriver \( \, 10^2 \, \), vilket betyder \( \, 10 \cdot 10 \, \), och istället för \( \, 10 \, \) skriver \( \, 10^1 \, \), ser man att det bildas en summa av termer där varje term har formen "(siffra \( \, 0\)-\(9 \, \)) multiplicerad med \( \, 10\)-potenser":

\[ {\color{Red} 3} \, \cdot 10^2 + {\color{Red} 1}\cdot 10^1 + {\color{Red} 2}\cdot 10^0 = 300 + 10 + 2\cdot 1 = {\color{Red} {312}} \, \]

Denna summa är en generell form för representation av tal i det decimala positionssystemet.

Exempel 2

Problem:

Ange talet \( \, 5\,689 \, \) som en summa av termer där varje term har formen "(siffra \( \, 0\)-\(9 \, \)) multiplicerad med \( \, 10\)-potenser".

Lösning:

\[{\color{Red} {5\,689}}\;=\;{\color{Red} 5}\cdot1000\,+\,{\color{Red} 6}\cdot100\,+\,{\color{Red} 8}\cdot10\,+\,{\color{Red} 9}\cdot1\;=\;{\color{Red} 5}\cdot10^3\,+\,{\color{Red} 6}\cdot10^2\,+\,{\color{Red} 8}\cdot10^1\,+\,{\color{Red} 9}\cdot10^0\]

Exempel 3

Problem:

Siffrorna i talet \( \, 96\,038 \, \) ska flyttas så att man får ett femsiffrigt tal som ligger så nära \( \, 40\,000 \, \) som möjligt.

Lösning:

De två siffrorna närmast \( \, 4 \, \) (första siffran i \( \, 40\,000\)) är \( \, 3 \, \) och \( \, 6 \, \).

Om vi börjar med siffran \( \, 6 \, \) skulle den ge värdet \( \, 60\,000 \, \) som är längre bort från 40 000 än om vi börjar med 3. Detta skulle nämligen ge värdet 30 000 som är närmare \( \, 40\,000 \, \). Därför bestämmer vi oss att stanna under \( \, 40\,000 \, \), då blir den första siffran i det tal vi söker, \( \, 3 \, \). Då får vi \( \, 30\,000 \, \).

För att komma så nära \( \, 40\,000 \, \) som möjligt tar vi som nästa siffra den största, nämligen \( \, 9 \, \). Då får vi \( \, 39\,000 \, \). Den näst största siffran är \( \, 8 \, \). Då blir det \( \, 39\,800 \, \). Slutligen är bara \( \, 6 \, \) och \( \, 0 \, \) kvar, så att det blir \( \, 39\,860 \, \).