3.5 Lösning 8a

     Vi inför ett koordinatsystem och sätter glasskivan i det, så här:

+++

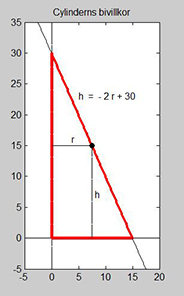
Vi inför ett koordinatsystem och sätter den röda triangeln från uppgiftens figur i den. Vi väljer cylinders radie \( \, r \, \) som horisontell och dess höjd \( \, h \, \) som vertikal axel. Kons mantellinje (från basytans kant till konens spets) blir då en rät linje. Punkten \( \, (x, y) \, \) rör sig på denna räta linje vars ekvation är: \[ {\color{Red} y} \, = \, k\,x \, + \, m \] Lutningen \( \, k \, = \, \displaystyle {\Delta y \over \Delta x} \, = \, - \, {20 \over 30} \, = \, - \, {2 \over 3} \) Skärningspunkten med \(\,y\)-axeln: \( \quad m \, = \, 20 \) Den räta linjens ekvation blir då: \( \displaystyle {\color{Red} y} \, = \, - \, {2 \over 3}\,x \, + \, 20 \)

Detta samband mellan \( \, x \, \) och \( \, {\color{Red} y} \,\) är problemets bivillkor.