1.3 Polynom i faktorform

Innehåll

1 Vad är en faktor?
2 Faktorisering av 2:a gradspolynom
3 Samband mellan koefficienter och nollställen
- 3.1 Exempel 1
- 3.2 Exempel 2
4 Dubbelrot
5 Det allmänna fallet (icke-normalform)
- 5.1 Exempel 3
6 Faktorisering av 3:e och högre gradspolynom
- 6.1 Exempel 4
- 6.2 Exempel 5
7 Internetlänkar

Vad är en faktor?

Du minns väl att ett uttryck av formen

\[ a \cdot b \]

är en produkt. Ingredienserna \(a\) och \(b\) kallas faktorer. Så länge \(a\) och \(b\) står som variabler (platshållare) för tal är uttrycket ovan en faktorform för tal. T.ex. är 3 \(\cdot\) 4 en faktorform för talet 12. Processen att ta fram produkten 3 \(\cdot\) 4 kallas faktorisering av talet 12.

En faktorisering av polynom innebär att skriva om polynomet, som ursprungligen är en summa av termer, till en produkt. T.ex.:

\[ x^2 - 7\,x + 12 = (x-3) \cdot (x-4) \]

Till vänster om likhetstecknet har vi polynomet som en summa av termer. Till höger står samma polynom som en produkt av faktorer. Den nya formen kallas polynom i faktorform och är resultat av faktorisering. Ingredienserna i faktorformen dvs faktorerna \( (x-3)\, \) och \( (x-4)\, \) är i sin tur polynom, fast av mindre grad, nämligen 1. Ursprungspolynomet är av grad 2, liknande faktorerna 3 och 4 som är mindre än 12. Man har splittrat upp det hela i sina beståndsdelar.

Matematiskt inser man likheten ovan genom att utveckla produkten:

\[ (x-3) \cdot (x-4) = x^2 - 4\,x - 3\,x + 3 \cdot 4 = x^2 - 7\,x + 12 \]

Men hur får man fram faktorformen från polynomet? Dvs: Hur faktoriserar man ett polynom? Frågan är relevant, därför att faktorformen för det första tillåter förenkling (förkortning) av komplexa uttryck och för det andra avslöjar viktiga egenskaper hos polynomet. Vi kommer att förstå det bättre i fortsättningen.

Faktorisering av 2:a gradspolynom

Sätter man polynomet \( x^2 - 7\,x + 12 \) till 0 uppstår följande ekvation:

\[ x^2 - 7\,x + 12 = (x-3) \cdot (x-4) = 0 \]

Denna ekvation är en inbjudan att söka de tal x för vilka polynomets värde är 0. Du minns väl att man kallar sådana x för polynomets nollställen. Därför är denna ekvations lösningar identiska med polynomets nollställen, vare sig man skriver polynomet som en summa av termer eller i faktorform. Faktorformen \((x-3) (x-4) \) har dock den stora fördelen att man kan se lösningarna till ekvationen ovan utan att behöva räkna. Det är nollproduktmetoden som gör detta möjligt. Den visar nämligen att 3 och 4 är lösningar till ekvationen \( (x-3) (x-4) = 0 \): För att produkten \( (x-3) (x-4) \) ska vara lika med 0 måste antingen den första faktorn \( (x-3) \) eller den andra faktorn \( (x-4) \) vara lika med 0. För att \( (x-3) \) eller \( (x-4) \) ska vara lika med 0 måste \( x \) antingen vara lika med 3 eller lika med 4. Detta i sin tur innebär att 3 och 4 är lösningar till ekvationen \( (x-3) (x-4) = 0 \). Pga likheten mellan polynom och dess faktorform måste 3 och 4 även vara polynomets nollställen dvs lösningar till ekvationen ovan. Men vad gör man om man inte än har faktorformen?

Resonemanget ovan ger oss nu en metod i handen for att få fram faktorformen från polynomet. För att faktorisera polynomet\( x^2 - 7\,x + 12 \) behöver vi bara beräkna dess nollställen, säg x1 och x2, och sedan skriva upp faktorformen \((x-x1) (x-x2) \). Låt oss genomföra det i vårt exempel:

\[\begin{align} x^2 - 7\,x + 12 & = 0 \\ x_{1,2} & = 3,5 \pm \sqrt{12,25 - 12} \\ x_{1,2} & = 3,5 \pm \sqrt{0,25} \\ x_{1,2} & = 3,5 \pm 0,5 \\ x_1 & = 4 \\ x_2 & = 3 \\ \end{align}\]

Därför har polynomet \( x^2 - 7\,x + 12 \) faktorformen \( (x-3) \cdot (x-4) \). Vi kommer att lära oss en effektivare metod för lösning av 2:a gradsekvationer och därmed för faktorisering av 2:gradspolynom, när vi lärt oss ett enkelt samband mellan ett polynoms koefficienter och dess nollställen (Vietas formler).

Det som vi genomförde för vårt exempel kan generaliseras till alla 2:gradspolynom, åtminstone sådana som är givna i normalform:

Sats (Faktorisering 2 nollställen):

Om 2:gradspolynomet \( x^2 + p\,x + q \) har nollställena \( x_1\, \) och \( x_2\, \) så gäller:

\[ x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) \]

För att bevisa satsen ovan kan man t.ex. sätta in 2:a gradsekvationens lösningsformel (pq-formeln) för \( x_1\, \) och \( x_2\, \) och utveckla produkten på högerledet. En jämförelse av koefficienter kommer att resultera i likhet med vänsterledet. Det finns motsvarande satser om polynom av högre grad än 2 som vi inte behandlar här.

Istället ska vi undersöka ett enkelt, men intressant samband mellan 2:a gradspolynomets koefficienter \( p\, \) och \( q\, \) och dess nollställen \( x_1\, \) och \( x_2\, \), vilket ger dig möjligheten att roa dina vänner genom att låta dem säga två tal, t.ex. 3 och 4, och omedelbart skriva upp den 2:a gradsekvation vars lösningar just är 3 och 4.

Samband mellan koefficienter och nollställen

Vi åter anknyter till likheten mellan polynom och dess faktorform som vi behandlade ovan (Faktorisering av 2: gradspolynom) genom att utveckla produkten:

\[ (x-3) \cdot (x-4) = x^2 - 4\,x - 3\,x + 3 \cdot 4 = x^2 - (3+4)\,x + 3 \cdot 4 = x^2 - 7\,x + 12 \]

Att vi i mellanräkningen, till synes onödigt, skriver \( x^2 - (3+4)\,x + 3 \cdot 4 \) beror på att vi vill förtydliga sambandet mellan polynomets koefficienter -7 och 12 å ena sidan och dess nollställen 3 och 4 å andra sidan: x-termens koefficient -7 är summan av 3 och 4 med omvänt förtecken. Polynomets konstanta term 12 är produkten till 3 och 4, dvs:

\[ 3 + 4 = 7 \qquad {\rm och} \qquad 3 \cdot 4 = 12 \]

På så sätt kan du roa dina vänner genom att låta dem säga två tal, t.ex. 3 och 4, och omedelbart skriva upp 2:a gradsekvationen

\[ x^2 - 7\,x + 12 = 0 \]

och låta dina vänner lösa ekvationen. De kommer att få just dessa två tal som lösningar. För att bilda ekvationen behöver du bara summera talen och sätta summan med omvänt förtecken framför x samt multiplicera talen med varandra och använda produkten som 2:a gradsekvationens konstanta term. Prova gärna med andra tal. Det kommer alltid att stämma, vilket inte är något trolleri utan resultat av följande generell matematisk sats:

Sats (Vietas formler):

Om 2:gradspolynomet \( x^2 + p\,x + q \) har nollställena \( x_1\, \) och \( x_2\, \) så gäller:

\[ x_1 + x_2 = -p \qquad {\rm och} \qquad x_1 \cdot x_2 = q \]

Bevis:

Genom att använda satsen som vi formulerade i slutet av förra paragrafen (Faktorisering 2 nollställen) kan vi skriva:

\[ x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) \]

Om vi nu utvecklar produkten på höger sidan kan vi skriva vidare:

\[ x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) = x^2 - x_2\,x - x_1\,x + x_1 \cdot x_2 = x^2 - (x_1+x_2)\,x + x_1 \cdot x_2 \]

En jämförelse av koefficienterna mellan polynomet \( x^2 - (x_1+x_2)\,x + x_1 \cdot x_2 \) (högerledet) och polynomet \( x^2 + p\,x + q \) (vänsterledet) ger resultatet:

\[ x_1 + x_2 = -p \qquad {\rm och} \qquad x_1 \cdot x_2 = q \]

Vad som skulle bevisas (V.s.b.).

Även denna sats kan generaliseras till polynom av högre grad än 2. Den franske matematikern François Viète|(1540-1603) var en av de första som såg sambandet mellan ett polynoms koefficienter och dess nollställen. Därför kallas formlerna \( x_1 + x_2 = -p\, \) och \( x_1 \cdot x_2 = q \) efter honom Vietas formler.

Er stor fördel av Vietas formler för oss är att man kan lösa 2:a gradsekvationer och därmed faktorisera polynom utan att behöva använda lösningsformeln. Detta innebär mindre räknearbete vilket i sin tur minskar risken för felräkning. På köpet går det fortare att ta fram polynomens faktorform.

Exempel 1

Ta ekvationen

\( x^2 - 7\,x + 10 = 0 \)

För lösningarna \( x_1\,\) och \( x_2\,\) måste enligt Vietas formler gälla\[ \begin{align} x_1 + x_2 & = -(-7) = 7 \\ x_1 \cdot x_2 & = 10 \end{align}\]

Vi måste alltså hitta två tal vars produkt är 10 och vars summa är 7. Med lite provande hittar man 2 und 5 eftersom \( 2 + 5 = 7\, \) och \( 2 \cdot 5 = 10 \). Prövning bekräftar resultatet.

Har vi på det här enkla sättet hittat nollställena till polynomet \( x^2 - 7\,x + 10 \) kan vi skriva upp faktorformen\[ x^2 - 7\,x + 10 = (x - 2) \cdot (x - 5) \]

Utveckling av produkten på höger sidan bekräftar faktoriseringen.

Exempel 2

Till ekvationen

\( x^2 - 6\,x + 9 = 0 \)

ger Vietas formler\[ \begin{align} x_1 + x_2 & = -(-6) = 6 \\ x_1 \cdot x_2 & = 9 \end{align}\]

Man hittar lösningarna \( x_1 = 3\,\) och \( x_2 = 3\,\) eftersom \( 3 + 3 = 6\,\) och \( 3 \cdot 3 = 9 \).

Därför kan polynomet \( x^2 - 6\,x + 9 \) faktoriseras så här\[ x^2 - 6\,x + 9 = (x - 3) \cdot (x - 3) = (x - 3)^2 \]

Det intressanta med detta exempel är att vi endast har en lösning x = 3 till 2:a gradsekvationen \( x^2 - 6 x + 9 = 0 \). Fast, om vi tittar på faktorformen \( (x - 3) (x - 3) = 0 \) kan man lika bra säga att vi har två identiska lösningar - en filosofisk skillnad som man matematiskt brukar lösa upp genom att kalla lösningen för en dubbelrot till ekvationen.

Dubbelrot

Sats (Faktorisering 1 nollställe):

Om 2:gradspolynomet \( x^2 + p\,x + q \) endast har ett nollställe \( x_1\, \) så gäller:

\[ x^2 + p\,x + q = (x-x_1)^2 \]

Ett sådant nollställe kallas för dubbelrot till ekvationen \( x^2 + p\,x + q = 0 \).

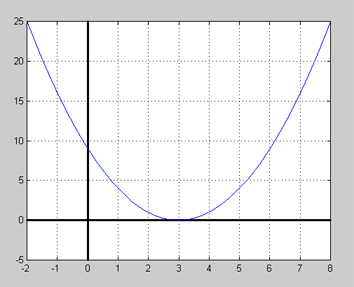
Dubbelrötter har vissa intressanta egenskaper. Låt oss börja att upptäcka dem genom att rita grafen till polynomfunktionen och undersöka på vilket sätt dubbelroten "skär" x-axeln. Vi tar polynomet från Exempel 2 ovan där ekvationen \( x^2 - 6\,x + 9 = 0 \) hade dubbelroten x = 3.

Så här ser grafen ut till polynomfunktionen \( y = x^2 - 6\,x + 9 \):

Grafen visar att kurvan inte skär utan bara berör x-axeln vid x = 3. Det är en av de typiska egenskaperna hos dubbelrötter. De ligger på gränsen mellan att skära (två lösningar) och inte skära x-axeln (ingen lösning alls). Matematiskt uttrycker sig denna egenskap i faktoriseringens form:

\[ x^2 - 6\,x + 9 = (x-3) \cdot (x-3) = (x-3)^2 \]

Den dubbla förekomsten av faktorn (x-3) ger roten dess namn dubbelrot.

Det allmänna fallet (icke-normalform)

Alla våra hittills behandlade polynom var i normalform, dvs den ledande koefficienten (kvadratiska termens koefficient eller talet framför x²) var alltid 1. Det behöver inte alltid vara så. Låt oss t.ex. faktorisera följande polynom med ledande koefficienten 3:

\[ 3\,x^2 - 6\,x - 9 \]

Lösningen består i att återföra problemet till den kända typen i normalform genom att bryta ut den ledande koefficienten:

\[ 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-x_1) \cdot (x-x_2) \]

där \((x-x_1) \cdot (x-x_2)\) är faktoriseringen av polynomet \( x^2 - 2\,x - 3 \). Efter att ha löst detta nya problem kan vi komma tillbaka och sätta in lösningen i ansatsen ovan för att få faktoriseringen av \( 3\,x^2 - 6\,x - 9 \).

För att få fram \( x_1\,\) och \( x_2\,\) som ger oss faktoriseringen av \( x^2 - 2\,x - 3 \) kan vi som vanligt använda Vietas formler\[ \begin{align} x_1 + x_2 & = -(-2) = 2 \\ x_1 \cdot x_2 & = -3 \end{align}\]

Man hittar lösningarna \( x_1 = 3\,\) och \( x_2 = -1\,\) eftersom \( 3 + (-1) = 2\,\) och \( 3 \cdot (-1) = -3 \).

Därför kan polynomet \( x^2 - 2\,x - 3 \) faktoriseras så här\[ x^2 - 2\,x - 3 = (x - 3) \cdot (x + 1) \]

Går vi tillbaka och sätter in denna lösning i det ursprungliga problemets ansats får vi det ursprungliga polynomets faktorisering:

\[ 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-3) \cdot (x+1) \]

Den ovan beskrivna metoden fungerar alltid när 2:a gradspolynomet har ett eller två nollställen. Har det däremot inget nollställe alls finns det inte heller någon faktorisering.

Exempel 3

Vad gör man om den ledande koefficienten "inte går att bryta ut" eftersom den inte delar de andra koefficienterna jämnt? Man gör det ändå och går över till tal i bråkform. Det finns nämligen ingen begränsning varken för polynomets nollställen eller koefficienter, när det gäller taltypen: De kan vara heltal, som var fallet hittills i våra exempel, men även bråk- eller decimaltal. Låt oss t.ex. faktorisera följande polynom med en ledande koefficient som inte delar de andra koefficienterna jämnt:

\[ 7\,x^2 - 5\,x - 2 \]

Vi bryter ut 7 och skriver det nya polynomets koefficienter i bråkform:

\[ 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x-x_1) \cdot (x-x_2) \]

För att få fram \( x_1\,\) och \( x_2\,\) använder vi Vietas formler\[ \begin{align} x_1 + x_2 & = {5 \over 7} \\ x_1 \cdot x_2 & = - {2 \over 7} \end{align}\]

Man hittar lösningarna \( x_1 = 1\,\) och \( x_2 = -{2 \over 7}\,\) eftersom \( 1 - {2 \over 7} = {5 \over 7} \) och \( 1 \cdot {-2 \over 7} = {-2 \over 7} \).

Så får vi det nya polynomets faktorisering\[ x^2 - {5 \over 7}\,x - {2 \over 7} = (x - 1) \cdot (x + {2 \over 7}) \]

Går vi tillbaka och sätter in detta i det ursprungliga problemets ansats får vi det ursprungliga polynomets faktorisering:

\[ 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x - 1) \cdot (x + {2 \over 7}) \]

Vill man i slutet bli av med bråktal kan man multiplicera in 7 i den andra parentesen och skriva faktoriseringen så här:

\[ 7\,x^2 - 5\,x - 2 = (x - 1) \cdot (7\,x + 2) \]

Faktorisering av 3:e och högre gradspolynom

Faktorisering av 2:a gradspolynom är alltid möjlig för oss eftersom vi kan lösa 2:a gradsekvationer. I de fall man lyckas återföra 3:e eller högre gradsekvationer till 2:a gradsekvationer är det även möjligt att faktorisera polynom av högre grad än 2. Ett sådant fall föreligger om man antingen känner till eller t.ex. med hjälp av grafen kan få fram åtminstone en lösning till en 3:e gradsekvation. Låt oss genomföra detta för följande exempel:

Problem: Faktorisera 3:e gradspolynomet

\[ P(x) = x^3 - 6\,x^2 + 5\,x + 12 \]

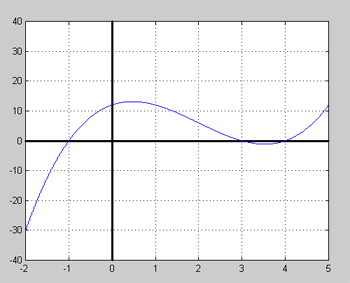
Lösning: För att få fram något av polynomets nollställen ritar vi

grafen till funktionen \( y = x^3 - 6\,x^2 + 5\,x + 12 \)

Grafen visar att polynomet har tre nollställen av vilka ett är ganska tydligt på bilden och kan avläsas till x = -1, medan de andra två är mindre tydliga. För att avgöra om detta nollställe är exakt gör vi en prövning genom att sätta in x = -1 i polynomet\[ P(-1) = (-1)^3 - 6\,\cdot\,(-1)^2 + 5\,\cdot\,(-1) + 12 = -1 - 6\,\cdot\,1 - 5 + 12 = -1 -6 -5 +12 = -12 +12 = 0 \]

Prövningen visar att x = -1 är ett exakt nollställe till P(x). Härav kan vi nu dra slutsatsen att de två andra nollställena måste uppfylla följande ekvation:

\[ P(x) = x^3 - 6\,x^2 + 5\,x + 12 = Q(x) \cdot (x+1) = 0 \]

där \( Q(x) \) är ett 2:a gradspolynom som vi inte känner till än. Denna slutsats baseras på en generell matematisk sats, algebrans fundamentalsats som säger att ett polynom av grad n har n nollställen. Vi kan med nollproduktmetoden resonera så här: För att produkten \( Q(x) \cdot (x+1) \) ska vara lika med 0 måste antingen \( Q(x) \) eller \( (x+1) \) vara lika med 0. Vi vet redan att \( (x+1) \) är 0 för x = -1 som är \( P(x) \):s ena nollställe. Alltså måste \( P(x) \):s andra två nollställen finnas i \( Q(x) \). Med andra ord de andra två nollställen måste vara det 2:a gradspolynomet \( Q(x) \):s nollställen. Kan vi bestämma \( Q(x) \), beräkna dess nollställen samt ställa upp dess faktorform, har vi faktoriserat även det 3:e gradspolynomet \( P(x) \). Vi har ju redan hittat ett nollställe och ställt upp en ansats till faktoriseringen av \( P(x) \) i form av ekvationen ovan. Vi bearbetar nu vidare denna ansats genom att införa i den för \( Q(x) \) den allmänna formen för ett 2:a gradspolynom\[ Q(x) = a\,x^2 + b\,x + c \]

där a, b och c är koefficienter som vi måste bestämma. Sätter vi in denna form i ansasten ovan får vi:

\[ x^3 - 6\,x^2 + 5\,x + 12 = (a\,x^2 + b\,x + c) \cdot (x+1) \]

Vi vet från förra avsnitt att två polynom är lika med varandra om alla deras motsvarande koefficienter, dvs de som tillhör termer av samma grad, överensstämmer. För att kunna genomföra denna jämförelse av koefficienter utvecklar vi produkten på höger sidan och ordnar termerna:

\[ x^3 - 6\,x^2 + 5\,x + 12 = a\,x^3 + b\,x^2 + c\,x + a\,x^2 + b\,x + c = a\,x^3 + (b+a)\,x^2 + (c+b)\,x + c \]

Jämförelse av koefficienterna på höger- och vänsterled ger:

\[ \begin{align} a & = 1 \\ b + a & = -6 \\ c + b & = 5 \\ c & = 12 \end{align}\]

Genom insättning av \( a = 1 \) i den andra och \( c = 12 \) i den tredje ekvationen får vi i båda fall b = -7. Därmed har vi bestämt polynomet \(Q(x)\)\[ Q(x) = x^2 - 7\,x + 12 \]

I början av detta avsnitt (Faktorisering av 2:a gradspolynom) hade vi faktoriserat det här polynomet till:

\[ x^2 - 7\,x + 12 = (x-3) \cdot (x-4) \]

Inför vi nu detta resultat i vår ansats i början får vi faktoriseringen för P(x):

\[ P(x) = x^3 - 6\,x^2 + 5\,x + 12 = Q(x) \cdot (x+1) = (x^2 - 7\,x + 12) \cdot (x+1) = (x-3)\,\cdot\,(x-4)\,\cdot\,(x+1) \]

Den ovan beskrivna metoden kan i princip även användas för faktorisering av polynom av högre grad än 3. Anledningen till det är algebrans fundamentalsats som vi redan nämnde tidigare och som lite förenklad lyder så här:

Sats (Algebrans fundamentalsats):

Ett polynom av grad n har exakt n nollställen \( x_1, \, x_2, \,\quad\ldots\, x_n \)och kan faktoriseras så här:

\[ a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad \ldots \quad + a_1 \cdot x + a_0\;=\;a_n \cdot (x-x_1) \cdot (x-x_2) \cdot\quad\ldots\quad \cdot (x-x_n) \]

Några anmärkningar måste göras till denna förenklade formulering av algebrans fundamentalsats:

Egentligen utgör endast den första delen (polynom av grad n har exakt n nollställen) algebrans fundamentalsats. Den andra delen om faktorisering är en följd av den.
Antalet n nollställen är räknade med multiplicitet, dvs dubbla rötter är räknade två gånger, tredubbla tre gånger osv.
Den fullständiga faktoriseringen i linjära faktorer \( (x-x_i)\, \) är endast möjlig i mängden av s.k. komplexa tal, en taltyp som inte behandlas i C-kursen. För oss som räknar med reella tal (största taltyp vi känner till) betyder der att vissa polynom endast kan faktoriseras till linjära och kvadratiska faktorer.

Exempel 4

\( P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x^2 - 4\,x + 13) \)

Polynomet P(x) har en dubbelrot x = 0, en enkel rot x = 1 och två s.k. komplexa rötter som ger upphov till den kvadratiska faktor som står sist. För oss räcker det att ange faktoriseringen i forman ovan. Vi kan få fram den med de metoder vi lärt oss i detta avsnitt: Den dubbla roten x = 0 får vi genom att bryta ut \( x^2 \), roten x = 1 kan vi t.ex. få via grafen samt en prövning. Den kvadratiska faktorns koefficienter kan vi beräkna med hjälp av jämförelse av koefficienter. Att det inte går att få fram en fullständig faktorisering i linjära faktorer beror på att den kvadratiska faktorn saknar reella rötter.

Exempel 5

Att vi ändå kan ha praktisk nytta av algebrans fundamentalsats visar följande exempel: I övning 6 i avsnittet 1.1 Ekvationer hade vi (förhoppningsvis) löst 4:e gradsekvationen

\( x^4 - 29\;x^2 = -100 \)

och fått lösningarna

\( x_1 = 5, \qquad x_2 = -5, \qquad x_3 = 2 \quad {\rm och} \quad x_4 = -2 \)

Vi kan skriva ekvationen som en polynomekvation

\( P(x) = x^4 - 29\;x^2 + 100 = 0 \)

Pga kännedomen om ekvationens lösningar som är identiska med polynomets nollställen, kan vi enligt algebrans fundamentalsats faktorisera 4:e gradspolynomet P(x) så här\[ P(x) = x^4 - 29\;x^2 + 100 = (x-5) \cdot (x+5) \cdot (x-2) \cdot (x+2) \]