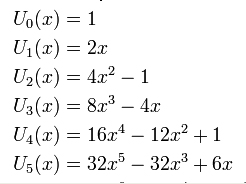1.1 Polynom

Teori

Övningar

Kapitel 1 Algebra och funktioner

Lektion 3 Polynom I

Lektion 4 Polynom II

Exempel på polynom

Uttrycken nedan kallas polynom:

\[ 4\,x + 12 \]

\[ 3\,x^2 + 5\,x - 16 \]

\[ 8\,x^3 + 4\,x^2 - 7\,x + 6\]

\[ 3\,x^4 - 8\,x^3 + 12\,x^2 - 54\,x + 9 \]

För läslighetens och strukturens skull brukar man inleda ett polynom med den högsta x-potensen och fortsätta i fallande ordning.

Uppgift: Utveckla följande uttryck till ett polynom\[ 4\,x^3 - 2\,x^2\,(2\,x + 6) + 7\,x\,(3 + 2\,x) \]

Lösning: Vi löser upp parenteserna, sammanfattar de termer som går att sammanfatta och ordnar x-potenserna i fallande ordning\[ 4\,x^3 - 2\,x^2\,(2\,x + 6) + 7\,x\,(3 + 2\,x) = \,4\,x^3 -\,4\,x^3\,-\,12\,x^2 +\,21\,x\,+\,14\,x^2 = 2\,x^2 +\,21\,x \]

Ett polynoms grad

Den högst förekommande x-potensen i ett polynom dvs den största exponenten till x bland polynomets alla termer kallas polynomets grad.

Polynomet \( x^4 - 29\;x^2 + 100 \) har graden 4 eftersom den högst förekommande x-potensen har exponenten 4.

I de inledande exemplen ovan har polynomen graderna 1, 2, 3 och 4 i den ordning som de är angivna.

Ett polynoms koefficienter

Talen framför x-potenserna kallas polynomets koefficienter.

Polynomet \( x^5 + 3\,x^4 - 8\,x^3 + 12\,x^2 - 54\,x + 9 \) har koefficienterna \(1\,\), talet framför \(x^5\,\), \(3\,\), talet framför \( x^4\, \), \(-8\,\), \(12\,\), \(-54\,\) och \(9\,\). Ett polynoms koefficienter definierar själva polynomet.

Ett polynoms värde

Till skillnad från graden - varje polynom har en och endast en fördefinierad grad - har ett polynom inte något givet värde för sig utan endast ett värde för något spcificerat x. Tar vi t.ex. ett av polynomen ovan, säg det 3:e gradspolynomet\[ U_3(x) = 8\,x^3 - 4\,x \]

kan vi beräkna dess värde för \( x = 0,5 \) så här\[ U_3(0,5) = 8 \cdot 0,5^3 - 4 \cdot 0,5 = 8 \cdot 0,125 - 2 = 1 - 2 = -1 \]

Man säger att \( -1 \) är polynomets värde för x = 0,5 vilket bekräftas av grafen ovan där förloppet för polynomet \( U_3(x) \) visas, se grön kurva med n = 3. Man ser att ett polynoms värde beräknas exakt på samma sätt som en funktions värde: Man sätter in ett värde för x i polynomets alla termer och beräknar enligt föreskrift polynomets värde. Det är inte konstigt, för ett polynom är också en funktion när det tilldelas ett y eller som ovan \( U_3(x) \). Av funktionsbegreppet framgår också följande:

För varje x-värde får man endast ett värde för polynomet. Däremot kan det bli att man för två olika x-värden får samma polynomvärde. T.ex. får vi samma värde 0 för polynomet \( U_2(x) = 4\,x^2 - 1 \) både för \( x = 0,5 \) och \( x = -0,5 \). Jämför med grafens blå kurva \( U_2(x) \) med n = 2.

Att räkna med polynom

Summan (resultat av addition), differensen (resultat av subtraktion) och produkten (resultat av multiplikation) av två (eller flera) polynom är igen ett polynom, därför att summan, differensen och produkten av två (eller flera) termer är igen en eller flera termer. Man räknar med polynom precis på samma sätt som man gör det med uttryck därför att polynom är en speciell form av uttryck.

Addition, subtraktion och multiplikation av polynom

Två polynom är givna\[ P_1(x) = 6\,x^2 + 2\,x - 3 \] och \( P_2(x) = -6\,x^2 - 3\,x + 4 \). Bilda deras summa, differens och produkt.

Summa:

\( P_1(x)\,+\,P_2(x) = (6\,x^2\,+\,2\,x\,-\,3)\,+\,(-6\,x^2\,-\,3\,x\,+\,4) = 6\,x^2\,+\,2\,x\,-\,3\,-\,6\,x^2\,-\,3\,x\,+\,4 = -\,x\,+\,1 \)

Differens:

\( P_1(x)\,-\,P_2(x) = (6\,x^2\,+\,2\,x\,-\,3)\,-\,(-6\,x^2\,-\,3\,x\,+\,4) = 6\,x^2\,+\,2\,x\,-\,3\,+\,6\,x^2\,+\,3\,x\,-\,4 = 12\,x^2\,+\,5\,x\,-\,7 \)

Produkt:

\( P_1(x)\,\cdot\,P_2(x) = (6\,x^2\,+\,2\,x\,-\,3)\,\cdot\,(-6\,x^2\,-\,3\,x\,+\,4) = -36\,x^4\,-\,18\,x^3\,+\,24\,x^2\,-\,12\,x^3\,-\,6\,x^2\,+\,8\,x\,+\,18\,x^2\,+\,9\,x\,-\,12 = \)

\( = -36\,x^4\,-\,30\,x^3\,+\,36\,x^2\,+\,17\,x\,-\,12 \)

Räkningarna ovan bygger på att först lösa upp parentserna och sedan sammanfoga de termer som går att sammanfoga, dvs de termer som har samma exponent. Att lösa upp parentserna innebär i additionsexemplet att ta bort parentserna utan åtgärd. Vid subtraktion däremot måste man vända om alla förtecken i den parentes som minustecknet står framför, allt enligt algebrans lagar för \( + \) och \( - \) . Vid multiplikation multipliceras varje term i den första parentesen in i den andra parentesen, dvs med alla termer i den, allt enligt algebrans distributivlag.

Som man ser blir alla resultat polynom. Vid addition och subtraktion blir resultatens grad samma eller mindre än utgångspolynomen. I additionsexemplet blir graden mindre eftersom de kvadratiska termerna tar ut varandra. Multiplikationen däremot förstorar graden. I vårt exempel är faktorerna \( P_1(x) \) och \( P_2(x) \) 2:a gradspolynom medan deras produkt blir av graden 4. Generellt gäller det att produktpolynomets grad blir m + n om faktorernas grader är m och n. I ord: graden av en produkt av två polynom är lika med summan av faktorernas grad.

Division av polynom ger inget polynom

Till skillnad från addition, subtraktion och multiplikation av två (eller flera) polynom som alltid ger ett polynom, ger division av två polynom i regel inte ett polynom. Det enklaste exemplet är uttrycket:

\[ 1 \over x \]

Detta uttryck kan å ena sidan uppfattas som kvoten (resultatet av division) mellan polynomet 1 (av graden 0) och polynomet x (av graden 1). Å andra sidan är \( 1/x \) enligt potenslagarna identiskt med:

\[ x^{-1}\, \]

Försöker man att identifiera detta som en term ser man att exponenten är negativ. Men ett polynoms termer måste ha exponenter till x som är positiva eller 0, se definitionen för term. Därför är uttrycket ovan inget polynom - ett exempel på att kvoten av två polynom i regel inte är polynom. Division av polynom leder oss till en ny klass av uttryck som \( 1/x \) eller \( x^{-1} \) är ett exempel på.

Denna nya klass av uttryck kallas rationella uttryck och kommer att behandlas senare i avsnitt 1.4.

Allmän definition

Ordet poly betyder på latin många och nom betyder term. Så polynom är närmare bestämt en summa av många termer. Ett exempel på term är följande:

\[ 8 \cdot x^3 \]

dvs en konstant gånger en x-potens. Generellt ser en term ut så här:

\[ a \cdot x^n \]

där n är ett positivt heltal eller 0. Dvs n får varken vara negativt eller ett bråk (decimaltal). Talet a kallas koefficient och är en godtycklig känd konstant. x däremot är en variabel som kan anta vilka värden som helst.

Som en summa av många sådana termer är ett polynom en speciell form av ett uttryck. Generellt har ett polynom av graden n följande form:

\[ a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad \ldots \quad + a_1 \cdot x + a_0 \]

där koefficienterna \( a_n\, \) är godtyckliga kända konstanter, n ett positivt heltal eller 0 och x en variabel. Den ledande termen är \( a_n \cdot x^n \) och den konstanta termen är \( a_0\, \). Även om det ur ren beräkningssynpunkt är helt irrelevant i vilken ordning man skriver ett polynoms termer, brukar man, för att hålla sig till en bra struktur, börja med den ledande termen, skriva termerna i avtagande exponentordning och avsluta med den konstanta termen. Om \( a_n = 1\,\) är polynomet i normalform.

Polynomfunktioner

När ett polynom tilldelas en annan variabel, säg y, ger det upphov till en speciell typ av funktion, kallad polynomfunktion. Närmare bestämt är polynomfunktioner en generalisering samt utvidgning av de funktionstyper vi sysslat hittills med. I Matte 1c-kursen hade vi bara linjära eller 1:a gradsfunktioner av typ\[ y = 4\,x + 12 \]

Till höger om likhetstecknet står ett polynom där \( x \) förekommer som 1:a gradspotens dvs med exponenten 1. Därför kallas \( 4 x^1 \) polynomets linjära term. Dess koefficient är 4. 12 kallas polynomets konstanta term. Grafen till denna 1:a gradsfunktion är en rät linje. I Matte B-kursen gick vi ett steg vidare och sysslade med 2:a gradsfunktioner av typ\[ y = 3\,x^2 + 5\,x - 16 \]

Här är 2 den högsta exponenten till \( x \). 3 är koefficienten till den kvadratiska termen \( 3 x^2 \), 5 är koefficienten till den linjära termen \( 5 x^1 \) och -16 är koefficienten till den konstanta termen \( -16 x^0 \). Grafen till denna 2:a gradsfunktion är en parabel. Redan dessa funktioner är polynomfunktioner utan att vi kallade dem så, därför att de är summor av termer som uppfyller de villkor som vi införde för n - nämligen att vara ett positivt heltal eller 0. Dvs vi har i Matte A och B sysslat med polynomfunktioner där n var 0, 1 eller 2, men inte högre. Om du undrar varför även konstanterna -16 och 12 i exemplen ovan kan anses som "termer" i den inledningsvis definierade bemärkelsen, kom ihåg att man kan skriva -16 som:

\[ -16 \cdot x^0 \]

Att man kan göra så beror på att \( x^0 = 1 \) enligt potenslagarna. Samma sak gäller för 12 som också är en term därför att 12 är lika med \( 12 x^0 \). Därmed har vi identifierat både \( 4 x + 12 \) och \( 3 x^2 + 5 x - 16 \) som polynom.

I Matte C-kursen ska vi nu lära oss att hantera även polynom av högre grad än 2. Vi tar exemplet från övning 6 i förra avsnitt 1.1 Ekvationer och gör om ekvationen där till polynomfunktionen\[ y = x^4 - 29\;x^2 + 100 \] vars graf ser ut så här:

Som man ser är grafen mer komplicerad än parabeln. Den har mer minima och maxima och mer nollställen som inte av en tillfällighet är identiska med lösningarna till 4:e gradsekvationen \( x^4 - 29\;x^2 = -100 \) i övning 6 (förra avsnitt 1.1 Ekvationer). Vi gjorde ju om denna ekvation till funktionen ovan så att ekvationens lösningar blev funktionens nollställen. Det känns naturligt att kalla polynomet \( x^4 - 29\;x^2 + 100 \) för ett 4:e gradspolynom, vilket leder oss till det allmänna begreppet grad av ett polynom.

Ett polynoms nollställen

När polynomets värde blir 0 kallar man de x för vilka polynomets värde blir 0, polynomets nollställen. Till skillnad från polynomets värde där vi satt in ett tal för x och fick ett värde för polynomet, måste vi nu vända på steken och sätta polynomet till ett värde, närmare bestämt till värdet 0 och beräkna x. Det är en mycket svårare uppgift eftersom vi måste lösa en ekvation som i regel är av högre grad. Vi är ju ute efter de x för vilka ett polynom av en viss grad blir 0. Dessa x är polynomets nollställen. Därför kan ett polynom ha flera nollställen medan ett polynoms värde är alltid unikt.

Exempel:

Bestäm alla nollställen till polynomet \( 5\,x^2 -\,20\,x \).

Att beräkna polynomets nollställen innebär att sätta polynomet till 0 och lösa följande ekvation\[ 5\,x^2 -\,20\,x = 0 \]

Eftersom vänsterledet saknar konstant term kan man bryta ut x som är den gemensamma faktorn i båda termer för att sedan kunna använda nollproduktmetoden\[\begin{align} 5\,x^2 -\,20\,x & = 0 \\ x\,(5\,x -\,20) & = 0 \\ x_1 & = 0 \\ 5\,x_2 -\,20 & = 0 \\ x_2 & = 4 \\ \end{align}\]

Polynomets nollställen är alltså \( x_1 = 0\, \) och \( x_2 = 4\, \).

En familj av polynom

Ett polynoms grad är ett mått på dess kompexitet. Ett exempel på hur kompexiteten växer med graden (från 0 till 5) är följande sex polynom vars grafer är ritade i samma koordinatsystem:

Man ser att kurvorna får fler maxima/minima ju högre deras grad är. Dessa polynom heter Chebyshevpolynom av 2:a slag efter den ryske matematikern Chebyshev som presenterade dem 1854. Att vi kallar dem för en familj av polynom beror på att de är relaterade till varandra med följande formel:

\[ U_n(x) = 2\,x\,\cdot\,U_{n-1}(x)\,-\,U_{n-2}(x) \qquad\qquad n = 2, 3, ... \]

\[ U_0(x) = 1, \quad U_1(x) = 2\,x \]

Om vi tittar på tabellen ovan ser man att polynomen \( U_n(x) \) bildar en följd där varje polynom har ett nummer n, kallat index (subscript som är skrivet nedsänkt). Formeln ovan ger oss möjligheten att ta fram Chebyshevpolynomen successivt, dvs vi kan ställa upp ett polynom med hjälp av de två föregående. I princip kan man ställa upp alla Chebyshevpolynom med denna formel utgående från de två första som är givna. Låt oss börja med att ställa upp det tredje (OBS! n = 2) med hjälp av de två första (n = 0 och 1)\[ \displaystyle U_0(x) = \underline{1} \]

\( U_1(x) = \underline{2\,x} \)

För n = 2 ger formeln ovan\[ U_2(x) = 2\,x\,\cdot\,U_1(x)\,-\,U_0(x) = 2\,x\,\cdot\,2\,x\,-\,1 = \underline{4\,x^2\,-\,1} \]

Sedan kan vi få fram \( U_3(x) \) genom att att sätta in n = 3 i formeln ovan\[ U_3(x) = 2\,x\,\cdot\;U_2(x)\,-\,U_1(x) = 2\,x\,\cdot\,(4\,x^2\,-\,1)\,-\,2\,x = 8\,x^3\,-\,2\,x\,-\,2\,x = \underline{8\,x^3\,-\,4\,x} \]

För n = 4 ger formeln ovan \( U_4(x) \) osv.\[ U_4(x) = 2\,x\,\cdot\,U_3(x)\,-\,U_2(x) = 2\,x\,\cdot\,(8\,x^3\,-\,4\,x)\,-\,(4\,x^2\,-\,1) = 16\,x^4\,-\,8\,x^2\,-\,4\,x^2\,+\,1 = \underline{16\,x^4\,-\,12\,x^2\,+\,1} \]

Så här kan man fortsätta för att få fram alla Chebyshevpolynom. Eftersom formeln som används bygger på att beräkna ett polynom från de två föregående kallar man den för polymens rekursionsformel, ett begrepp som används i samband med följder och summor (kap 5). Man kan säga att följden av Chebyshevpolynomen definieras av rekursionsformeln ovan.

Jämförelse av koefficienter

Med likhet mellan polynom menar man en algebraisk identitet mellan polynomen. Två polynom av samma grad:

\[ P(x) = a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad \ldots \quad + a_1 \cdot x + a_0 \]

och

\[ Q(x) = b_n \cdot x^n + b_{n-1} \cdot x^{n-1} + \quad \ldots \quad + b_1 \cdot x + b_0 \]

är lika med varandra om alla deras motsvarande koefficienter, dvs de som tillhör termer av samma grad, överensstämmer, närmare bestämt om:

\[ a_n = b_n, \quad a_{n-1} = b_{n-1}, \quad \ldots \quad a_1 = b_1, \quad a_0 = b_0 \]

Exempel 1

Två polynom är givna\[ P(x) = a \cdot x + 2\,a + b \]

\( Q(x) = 2\,x + 1\!\, \).

För vilka värden på \( a\, \) och \( b\, \) är de två polymen lika med varandra?

Vi skriver \( P(x),\, \) och \( Q(x)\, \) så att vi lättare kan se motsvarande koefficienter\[ P(x) = a \cdot x^1 + (2\,a + b) \cdot x^0 \]

\( Q(x) = 2 \cdot x^1 + \quad\;\; 1 \quad\;\; \cdot x^0 \)

Jämförelse av koefficienterna till \( x^1\, \) leder till\[ a = 2\,\]

Jämförelse av koefficienterna till \( x^0 \,\) leder till\[ 2\,a + b = 1\!\,\]

Sätter man in \( a = 2\, \) i denna relation får man \( b = -3\, \).

Polynomen \( P(x)\, \) och \( Q(x)\, \) är lika med varandra för\[ a = 2\, \]

\( b = -3\, \)

Metoden kallas jämförelse av koefficienter och är ett viktigt verktyg för att lösa högre gradsekvationer genom att faktorisera högre gradspolynom, se övningarna 10 och 11.

Exempel 2

Problem: Följande 3:e gradspolynom är givet\[ P(x) = x^3 + 4\,x^2 + x - 26 \]

Hitta ett 2:a gradspolynom \( Q(x)\, \) så att:

\[ Q(x)\cdot (x-2) = P(x) \]

Svar: \( Q(x) = x^2 + 6 \, x + 13 \)

Lösning:

Det 2:a gradspolynomet \( Q(x)\, \) kan skrivas så här\[ Q(x) = a\,x^2 + b\,x + c \]

Vi bestämmer koefficienterna \( a\, , \, b\, \) och \( c\, \) så att \( Q(x)\cdot (x-2) = P(x) \)

\(\begin{align} Q(x) \cdot (x - 2) & = (a\,x^2 + b\,x + c)\cdot (x - 2) = a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c = \\ & = a\,x^3 + (b - 2\,a)\,x^2 + (c - 2\,b)\,x - 2\,c = \\ & = a \cdot x^3 + (b - 2\,a) \cdot x^2 + (c - 2\,b) \cdot x - 2\,c \cdot x^0 \\ P(x) & = 1 \cdot x^3 + \quad\;\; 4 \quad\;\; \cdot x^2 + \quad\;\; 1 \quad\;\; \cdot x - 26 \cdot x^0 \end{align} \)

Jämförelse av koefficienterna till \( x^3 \)-termen ger:

\[\begin{align} a & = 1 \end{align} \]

Jämförelse av koefficienterna till \( x^2 \)-termen ger:

\[\begin{align} b - 2\, a & = 4 \\ b - 2\cdot 1 & = 4 \\ b - 2 & = 4 \\ b & = 6 \\ \end{align} \]

Jämförelse av koefficienterna till \( x^1 \)-termen ger:

\[\begin{align} c - 2\, b & = 1 \\ c - 2\cdot 6 & = 1 \\ c - 12 & = 1 \\ c & = 13 \\ \end{align} \]

Jämförelse av koefficienterna till \( x^0 \)-termen bekräftar värdet på c:

\[\begin{align} - 2\,c & = - 26 \\ c & = 13 \\ \end{align} \]

Vi får \( a = 1\, , \, b = 6\, \) och \( c = 13\, \) och därmed\[ Q(x) = x^2 + 6 \, x + 13 \]

Internetlänkar

http://www.mathsisfun.com/algebra/polynomials.html

http://www.youtube.com/watch?v=IDpnNnjFB1c

http://www.coolmath.com/algebra/algebra-practice-polynomials.html

http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut6_poly.htm

http://tutorial.math.lamar.edu/Classes/Alg/Polynomials.aspx

Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.