1.1 Lösning 4c

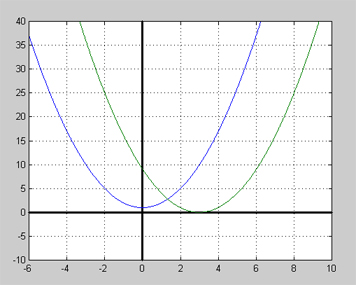
Graferna till \( \displaystyle y_1 = x^2 + 1 \) och \( \displaystyle y_2 = (x - 3)^2 \) ritade i samma koordinatsystem:

Bilden visar att kurvorna \( \displaystyle y_1 = x^2 + 1 \) (blå) och \( \displaystyle y_2 = (x - 3)^2 \) (grön) skär varandra i en punkt. Detta innebär att ekvationen

\( \displaystyle x^2 + 1 = (x - 3)^2 \)

har en lösning som kan avläsas från grafen till ca. \( \displaystyle x = 1,3 \). Men denna ekvation uppstår när man kvadrerar den ursprungliga rotekvationen

\( \sqrt{x^2 + 1} = x - 3 \)

Dvs den kvadrerade ekvationen har en lösning som är den ursprungliga rotekvationens falska rot \( \displaystyle x = 4 \over 3 \), se övning 4a.