3.5 Lösning 6b
Från Mathonline
Version från den 2 februari 2015 kl. 11.09 av Taifun (Diskussion | bidrag)
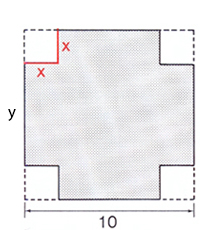
Vi inför beteckningen \( \, y \, \) för bassidan av den öppna lådan som ska byggas:
Då kan problemets bivillkor formuleras så här:
- \[ y \, = \, 10 \, - \, 2\,x \, \]
eftersom kartongens sida är \( \, 10 \; {\rm dm} \, \) lång varav \( \, 2\,x \, \) skärs ut, så att \( \, y \, \) blir bassidan av den öppna lådan som ska byggas.
Rektangelns andra sida som är parallell till muren har längden:
- \[ \, 9 \, - \, 2\,x \, \]
eftersom stängseln är \( \, 9 \; {\rm m} \, \) lång varav endast \( \, 2\,x \, \) går åt sidorna som är vinkelräta mot muren.
Därmed blir rektangelns area \( \, = \, x \cdot (9 \, - \, 2\,x) \, \)
Eftersom det är rektangelns area som ska maximeras är problemets målfunktion:
- \[ \, A(x) \, = \, x \cdot (9 \, - \, 2\,x) \, \]