Skillnad mellan versioner av "3.5 Extremvärdesproblem"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 1: | Rad 1: | ||
| − | + | __NOTOC__ | |
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
Versionen från 13 juni 2020 kl. 16.56
| << Förra avsnitt | Genomgång | Övningar |
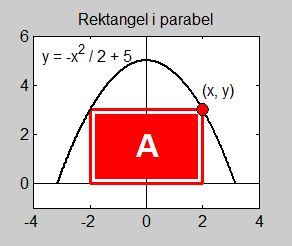
Exempel 1 Rektangel i parabel
En rektangel är inbunden i en parabel vars ekvation är given:
Punkten \( \, (x,\,y) \, \) rör sig på parabeln, se figuren. Placera den så att rektangelns area \( \, A \, \) blir maximal.
b) Bestäm \( \, x \, \) så att \( \, A(x) \, \) blir maximal. c) Beräkna rektangelns maximala area. |
|
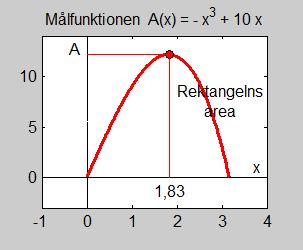
d) Bestäm definitionsmängden till funktionen \( \, A(x) \, \) och rita grafen till \( \, A(x) \). Markera maximipunkten från b) i grafen.
- Kontrollera algebraiskt om maximipunkten ligger inom definitionsmängden.
Lösning:
a) Rektangelns area kan skrivas som \( \quad A\,(x, \, {\color{Red} y}) \; = \; 2 \, \cdot x \, \cdot \, {\color{Red} y} \)
- Men \( \, A\,(x, \, {\color{Red} y}) \, \) är en funktion av två variabler som vi inte kan hantera.
- Därför måste \( A\,(x, \, {\color{Red} y}) \, \) skrivas om till en funktion \( \, A\,(x) \, \) av endast en variabel, nämligen \( \, x \).
- Detta gör vi genom att eliminera \( \, {\color{Red} y} \, \): Vi utnyttjar sambandet mellan \( \, x \, \) och \( \, {\color{Red} y} \, \) som är givet av parabelns ekvation.
- Rektangelns "rörliga" hörn \( \, (x,\,{\color{Red} y}) \, \) måste alltid ligga på parabeln. Därför måste \( \, x \, \) och \( \, y \, \) uppfylla parabelns ekvation:
\( \displaystyle {\color{Red} y} \, = \, -\,{\, x^2 \over 2} \, + \, 5 \) |
\( \qquad \) | Detta samband kallas för problemets bivillkor. |
Bivillkor för ett extremvärdesproblem
Ett extremvärdesproblems bivillkor är ett samband som bestäms av problemets givna geometriska
eller andra föreskrivna egenskaper.
Bivillkoret sätter restriktioner (begränsningar, eng. constraints) på punkten \( (x,\,y)\):s rörelsefrihet.
- I Exempel 1 är parabelns ekvation problemets bivillkor, därför att punkten \( (x,\,y) \) måste följa parabeln, se figuren ovan.
- Vi använder bivillkoret för att skriva om rektangelns area från en funktion av två variabler \( \, x \, \) och \( \, y \, \) till en funktion av en variabel \( \, x \).
- Därför sätter vi in parabelns ekvation \( \, \displaystyle {\color{Red} y} = -\,{\, x^2 \over 2} + 5 \, \) i rektangelns area \( \, A\,(x, \, {\color{Red} y}) = 2\cdot x \cdot {\color{Red} y} \, \) för att eliminera \( \, {\color{Red} y} \,\):
- \[ A\,(x, \, {\color{Red} y}) \, = \, 2 \cdot x \cdot {\color{Red} y} \, = \, 2 \cdot x \cdot \left({\color{Red} {-\,{\, x^2 \over 2} \, + \, 5}}\right) \, = \, -\,x^3 \, + \, 10\,x \]
- På så sätt får vi en funktion för rektangelns area som endast beror av \( \, x \):
\( A\,(x) \, = \, \displaystyle -\,x^3 \, + \, 10\,x \) |
\( \qquad \) | Denna funktion kallas för problemets målfunktion |
Målfunktion för ett extremvärdesproblem
Ett extremvärdesproblems målfunktion är alltid den funktion av endast en variabel som ska
maximeras eller minimeras.
Extremvärdesproblem består i regel av ett bivillkor och en målfunktion.
Bivillkoret används för att reducera målfunktionen till en funktion av endast en variabel.
- I Exempel 1 är \( A\,(x) \) problemets målfunktion, därför att det är rektangelns area som ska maximeras.
I \( A\,(x) \) är parabelns ekvation redan "inbakad".
b) För att hitta målfunktionens lokala maximum deriverar vi \( \, A(x) \, \) och bestämmer derivatans nollställen:
|
\( \qquad \) | Derivatans nollställen:
|
\( \qquad \) | \(\begin{array}{rcrcl} A'(x) & = & -3\,x^2 \, + \, 10 & = & 0 \\ & & 10 & = & 3\,x^2 \\ & & {10 \over 3} & = & x^2 \\ & & x_{1, 2} & = & \sqrt{10 \over 3} \\ & & x_1 & = & 1,83 \\ & & x_2 & = & -1,83 \end{array}\) |
\( \quad\; x_2 = -1,83 \, \) förkastas därför att arean och därmed \( \, x \, \) inte kan vara negativ, se även d).
- Vi sätter in \( \, x_1 = 1,83 \, \) i andraderivatan och använder reglerna om max/min:
\( \qquad\quad A''(1,83) = -6 \cdot 1,83 \, < \, 0 \quad \Longrightarrow \quad A(x) \, \) har ett lokalt maximum i \( \; \boxed{x \, = \, 1,83} \, \).
- För \( \, x = 1,83 \, {\rm cm} \, \) antar målfunktionen (rektangelns area) sitt maximum.
c) För att bestämma rektangelns maximala area sätter vi in \( \, x = 1,83 \, \) i målfunktionen \( \, A(x) \):
- \[ A\,(x) \, = \, \displaystyle -\,x^3 \, + \, 10\,x \]
- \[ A(1,83) = -\,1,83\,^3 \, + \, 10 \cdot 1,83 \, = \, 12,17 \]
- Rektangelns maximala area är \( \, 12,17 \, \).
|
d) Målfunktionen \( \, A\,(x) = \displaystyle -\,x^3 \, + \, 10\,x \, \) har definitionsintervallet: \( \, 0 \, \leq \, x \, \leq \, \sqrt{10} \)
|
 |
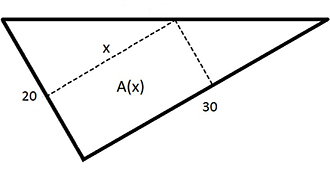
Exempel 2 Glasskiva (rektangel i triangel)
| En glasskiva har formen av en rätvinklig triangel med följande mått:
\( \qquad\qquad\qquad\quad \) Kortare kateten \( \, = \, 20 \, \) cm \( \qquad\qquad\qquad\quad \) Längre kateten \( \, = \, 30 \, \) cm En rektangulär glasplatta med maximal area ska skäras ut ur skivan. a) Formulera problemets bivillkor. b) Ställ upp problemets målfunktion. Ange dess definitionsmängd. |
 |
c) Bestäm \( \, x \, \) så att glasplattans area \( \, A(x) \, \) maximeras.
d) Beräkna glasplattans maximala area.
Lösning:
a) Vi inför beteckningen \( \; {\color{Red} y} \; \) för glasplattans andra sida, så att rektangelns area kan skrivas som \( \; A\,(x, {\color{Red} y}) \; = \; x \; \cdot \; {\color{Red} y} \)
För att skriva om funktionen ovan till en funktion \( \, A\,(x) \, \) av endast en variabel, nämligen \( \, x \, \),
måste \( \, {\color{Red} y} \, \) uttryckas med \( \, x \, \), så att \( \, {\color{Red} y} \, \) kan elimineras.
Sambandet mellan \( \, x \, \) och \( \, {\color{Red} y} \, \) bestäms av rektangelns "rörliga" hörn som är bundet till triangelns hypotenusa.
Vi inför ett koordinatsystem och sätter glasskivan i det, se bilden:
| Triangelns hypotenusa blir då en del av en rät linje.
Punkten \( \, (x, y) \, \) rör sig på denna räta linje vars ekvation är:
Lutningen \( \, k \, = \, \displaystyle {\Delta y \over \Delta x} \, = \, - \, {20 \over 30} \, = \, - \, {2 \over 3} \) Skärningspunkten med \(\,y\)-axeln: \( \quad m \, = \, 20 \) Den räta linjens ekvation blir då problemets bivillkor:
|
|
b) Det ovan formulerade bivillkoret för glasskivan sätts in i \( \; A\,(x, {\color{Red} y}) = x \cdot {\color{Red} y} \; \) för att eliminera \( \, {\color{Red} y} \,\)
och ställa upp ett uttryck för arean som endast beror av \( \, x \):
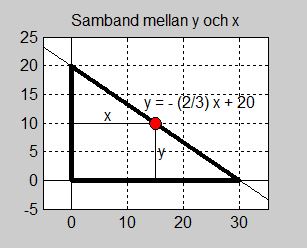
- \[ A\,(x, \, {\color{Red} y}) \, = \, x \cdot {\color{Red} y} \, = \, x \cdot \left(-\,{2 \over 3}\,x \, + \, 20\right) \, = \, -\,{2 \over 3}\,x^2 \, + \, 20\,x \]
c) För att hitta målfunktionens lokala maximum deriverar vi \( \, A(x) \, \) och bestämmer derivatans nollställen:
|
\( \qquad \) | Derivatans nollställen:
|
\( \qquad \) | \(\begin{array}{rcrcl} A'(x) & = & -{4 \over 3}\,x + 20 & = & 0 \\
& & 20 & = & {4 \over 3}\,x \\
& & {20 \, \cdot \, 3 \over 4} & = & x \\
& & x & = & 15
\end{array}\)
|
\( \, x = 15 \, \) som ligger inom målfunktionens definitionsmängd, sätts in i andraderivatan enligt reglerna om max/min:
\( A''(15) = \displaystyle -\,{4 \over 3} \,<\, 0 \quad \Longrightarrow \quad A(x) \, \) har ett lokalt maximum i \( \; \boxed{x \, = \, 15} \, \).
För \( \, x = 15 \, {\rm cm} \, \) antar målfunktionen ett maximum, dvs rektangelns area blir maximal.
d) Eftersom rektangeln får sin största area för \( \, x = 15 \, \) sätter vi in \( \, x = 15 \, \) i målfunktionen för att få största arean:
- \[ A\,(x) \, = \, \displaystyle -\,{2 \over 3}\,x^2 \, + \, 20\,x \]
- \[ A(15) = -\,{2 \over 3} \cdot 15^2 + 20 \cdot 15 = 150 \]
Glasplattans största area blir \( \, 150 \, {\rm cm}^2 \, \).
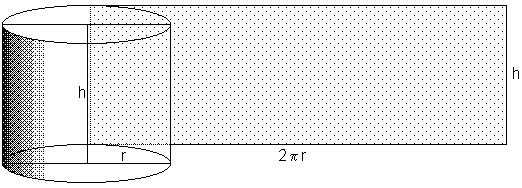
Exempel 3 Konservburk
| En cylinderformad konservburk ska produceras av en bit plåt. Vi antar:
Plåtens area \( \, = \, \) cylinderns begränsningsarea \( \, {\color{Red} {= \, 500 \, {\rm cm}^2}} \, \) efter spill. Vilka mått på cylindern måste väljas så att volymen blir maximal ?
b) Ställ upp problemets målfunktion. c) Bestäm cylinderns radie och höjd så att burkens volym
|
|
d) Ange målfunktionens definitionsmängd. Rita graferna till bivillkoret och målfunktionen. Tolka graferna.
e) Beräkna konservburkens maximala volym.
f) Vilket samband råder mellan cylinderns radie \( \, r \, \) och dess höjd \( \, h \, \) när volymen maximeras?
Lösning:
a) Begränsningsarean \( \, A \, = \, 2\,\pi\,r\,h \, + 2\,\pi\,r^2 \, = \, 500 \)
\( h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r \)
|
|
b) Cylinderns volym \( \, V \, \) är basytan \( \times \) höjden dvs: \( \qquad V\,(r, \, {\color{Red} h}) \; = \; \pi \, r^2 \; \cdot \; {\color{Red} h} \qquad \) Funktion av två variabler: \( \, r \, \) och \( \, {\color{Red} h} \, \).
För att skriva om denna funktion till en funktion av endast en variabel, sätter vi in bivillkoret från a) i \( \, V\,(r, \, {\color{Red} h}) \, \) och eliminerar \( \, {\color{Red} h} \, \):
- \[ V\,(r, \, {\color{Red} h}) \, = \, \pi \, r^2 \; \cdot \; {\color{Red} h} \, = \, \pi\,r^2\cdot \left( {\color{Red} {{250 \over \pi\,r}\,-\, r}} \right) \, = \, {250 \cdot \pi\,r^2 \over \pi\,r} \, - \, \pi\,r^3 \, = \, 250 \cdot r \, - \, \pi\,r^3 \]
c) Målfunktionen maximeras:
|
\( \qquad \) | Derivatans nollställen:
|
\( \qquad \) | \(\begin{array}{rcrcl} V'(r) & = & 250 \, - \, 3\,\pi\,r^2 & = & 0 \\ & & 250 & = & 3\,\pi\,r^2 \\ & & {250 \over 3\,\pi} & = & r^2 \\ & & r_{1, 2} & = & \pm\,\sqrt{250 \over 3\,\pi} \\ & & r & = & 5,15 \end{array}\) |
\( r_2 = -5,15 \, \) förkastas, för radien kan inte bli negativ. \( \, r = 5,15 \, > \, 0 \, \) sätts in i andraderivatan enligt reglerna om max/min:
\( V''(5,15) = -6 \,\pi\cdot 5,15 \, < \, 0 \quad \Longrightarrow \quad V(r) \, \) har ett lokalt maximum för \( \, r = 5,15 \).
För att få cylinderns höjd när volymen maximeras sätter vi in \( \, r = 5,15 \, \) i bivillkoret från a):
- \[ h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r \, = \, {250 \over \pi\cdot 5,15} \, - \, 5,15 \, = \, 10,30 \]
Cylinderns volym blir maximal för radien \( \quad \boxed{r = 5,15 \; {\rm cm}} \quad \) och höjden \( \quad \boxed{h = 10,30 \; {\rm cm}} \quad \).
d) För att bestämma målfunktionens definitionsmängd tittar undersöker vi bivillkoret: \( \qquad h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r \)
Av detta framgår att \( \, r \, \) inte får vara \( \, 0 \, \): \( \; r \, \neq \, 0 \; \). Därför är \( \, 0 \, \) en undre gräns för \( \, r \): \( \qquad r \, > \, 0 \)
För att hitta en övre gräns (största möjliga värde) för \( \; r \; \) tittar vi på cylinderns begränsningsarea:
- \[ \, A \, = \, 2\,\pi\,r\,h \, + 2\,\pi\,r^2 \, = \, 500 \]
Pga begränsningsareans konstanta värde \( \, 500 \, \) blir cylinderns radie störst när höjden blir \( \, 0 \, \).
Därför får vi radiens störst möjliga värde om vi i formeln ovan väljer \( \, h=0 \):
- \[ \, h = 0 \qquad \Longrightarrow \qquad A \, = \, 2\,\pi \cdot \left(r\right)\,^2 \, = \, 500 \qquad \Longrightarrow \qquad r \, = \, \sqrt{500 \over 2\,\pi} \, = \, 8,92 \]
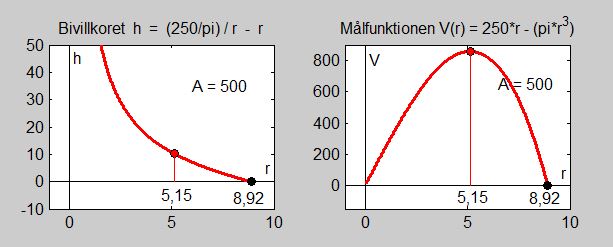
Grafen till vänster visar bivillkoret \( h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r \) och till höger målfunktionen \( V(r) \, = \, 250 \, r \, - \, \pi\,r^3 \), båda med definitionsmängden ovan.
Målfunktionens graf till höger bekräftar det algebraiska resultatet från c), nämligen att volymen blir maximal för \( \, r = 5,15 \).
Bivillkorets graf till vänster bekräftar att för \( \, r = 5,15 \, \) höjden blir \( \, \approx \, 10 \) och dessutom att \( \, r \, \) inte kan bli större än \( \, 8,92 \).
e) Resultaten från c) sätts in i målfunktionen för att få cylinderns största volym:
- \[ V(5,15) \, = \, \pi \, \cdot 5,15^2 \, \cdot 10,30 \, = \, 858,23 \]
Konservburkens maximala volym blir \( \; 858,23 \, {\rm cm}^3 \; \).
f) Följande samband råder mellan cylinderns radie \( \; r = 5,15 \, {\rm cm} \; \) och dess höjd \( \; h = 10,30 \, {\rm cm}\)
när volymen till en cylinder med en begränsningsarea på \( \, 500 \, {\rm cm}^2 \, \), maximeras:
- \( 2 \; r \; = \; h \)
Återstår frågan som är föremål för undersökning i övning 9, om samma samband även råder generellt mellan radien \( \; r \; \) och höjden \( \; h \; \) för alla konservburkar med vilken begränsningsarea som helst och maximal volym, nämligen:
- Diametern \( \; = \; \) Höjden
En annan intressant frågeställning är:
Råder även sambandet ovan om man utgår från en konservburk med fast given volym vars materialåtgång ska minimeras?
En närmare undersökning liknande lösningen till Exempel 3 kommer att visa att detta är fallet.
Dvs sambandet ovan är alltid optimalt ur ekonomisk synpunkt.
Ett ekonomiskt exempel
Se övning 7.
Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.
