Skillnad mellan versioner av "1.5 Bråkräkning"

Från Mathonline
Hoppa till: navigering, sök
m
m
Rad 9: Rad 9:
 
|}
 
|}
  
 +
 +
== <b><span style="color:#931136">Tal i bråkform</span></b> ==
 +
<br>
  
 
<math> \qquad\quad </math><div class="ovnE">
 
<math> \qquad\quad </math><div class="ovnE">
 
[[Image: Bild Tal i brakform 30.jpg]]
 
[[Image: Bild Tal i brakform 30.jpg]]
  
−
<big>Bråkstrecket betyder division<span style="color:black">:</span>
+
Bråkstrecket betyder division:
  
−
<math> \quad\; \displaystyle \frac{{\color{Limegreen} 3}}{{\color{Red} 4}} \; = \; {\color{Limegreen} 3} \, / \, {\color{Red} 4} \; = \; 0,75 </math></big>
+
<big><math> \quad\; \displaystyle \frac{{\color{Limegreen} 3}}{{\color{Red} 4}} \; = \; {\color{Limegreen} 3} \, / \, {\color{Red} 4} \; = \; 0,75 </math></big>
 
</div>
 
</div>
 +
 +
<big>
 +
Generellt:
 +
<div class="border-divblue">
 +
Alla tal i bråkform kan skrivas i decimalform, men inte tvärtom.
 +
</div>
 +
T.ex. <math> \quad\sqrt{2} = 1,4142135623730950488\ldots \quad </math> kan inte anges i bråkform eftersom det har en oändlig [[1.3_Decimaltal%2B#Icke-periodisk_decimalutveckling|<b><span style="color:blue">icke-periodisk decimalutveckling</span></b>]].
 +
 +
Alla tal som kan skrivas i bråkform kallas för <b><span style="color:red">rationella</span></b>. De som inte kan skrivas i bråkform kallas för <b><span style="color:red">irrationella</span></b>, se [[1.1_Om_tal#Olika_typer_av_tal|<b><span style="color:blue">Olika typer av tal</span></b>]].
 +
</big>
 +
 +
 +
== <b><span style="color:#931136">Blandad form</span></b> ==
 +
<br>
 +
<div class="ovnC">
 +
<big>Skriv bråket <math> \; \frac{7}{2} \; </math> till blandad form:</big>
 +
 +
<math> \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \; \color {Limegreen} 3 \,, {\rm rest} \; 1 \; = \; \boxed{\color {Limegreen} 3 \,\frac{1}{\color {Red} 2}} \quad </math>
 +
 +
<math> \quad </math> Eller använd miniräknare<span style="color:black">:</span>
 +
 +
<math> \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \quad\; 3,5 \quad\; = \; \color {Limegreen} 3 \,\frac{1}{\color {Red} 2} \quad </math>
 +
</div>
 +
 +
<big>
 +
<b><span style="color:#931136">OBS!</span></b>
 +
<div class="border-divblue">
 +
I blandade former står mellan heltalet och
 +
 +
bråket ett osynligt <big><big><span style="color:red">+</span></big></big>&nbsp;:&nbsp; <math> \quad \displaystyle \color {Limegreen} 3 \,\frac{1}{\color {Red} 2} \; = \; \color {Limegreen} 3 </math> <big><big><span style="color:red">+</span></big></big> <math> \displaystyle \frac{1}{\color {Red} 2} \quad </math>
 +
 +
Läs därför: &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; "Tre <b><span style="color:red">och</span></b> en halv"
 +
</div>
 +
 +
 +
<b><span style="color:#931136">Omvänt:</span></b></big>
 +
<div class="ovnC">
 +
<big>Skriv blandade formen till bråk:</big>
 +
 +
<math> \quad \displaystyle \boxed{\color {Limegreen} 3\,\frac{1}{\color {Red} 2}} \;\; = \;\; \frac{\color {Limegreen} 3 \, \cdot \color {Red} 2 \quad + \quad 1}{\color {Red} 2} \;\; = \;\; \frac{7}{\color {Red} 2} </math>
 +
 +
<math> \quad </math> Därför att<span style="color:black">:</span>
 +
 +
<math> \quad \displaystyle \color {Limegreen} 3\,\frac{1}{\color {Red} 2} \; = \; \color {Limegreen} 3 \; + \; \frac{1}{\color {Red} 2} = \frac{\color {Limegreen} 3}{1} + \frac{1}{\color {Red} 2} \; = </math>
 +
 +
<math> \qquad\;\;\, \displaystyle \; = \; \frac{\color {Limegreen} 3 \cdot \color {Red} 2}{1 \cdot \color {Red} 2} \; + \; \frac{1}{\color {Red} 2} \; = \; \frac{6}{\color{Red} 2} \; + \; \frac{1}{\color{Red} 2} \; = \; \frac{7}{\color{Red} 2} </math>
 +
</div>
 +
 +
 +
<big>
 +
<b><span style="color:#931136">Regeln för att skriva en blandad form till bråk:</span></b>
 +
<div class="border-divblue">
 +
 +
<math> \quad \displaystyle \color {Limegreen} a\;\frac{b}{\color {Red} c} \quad = \quad \frac{\color {Limegreen} a \, \cdot \color {Red} c \quad + \quad b}{\color {Red} c} \quad </math>
 +
</div>
 +
</big>
  
  
Rad 23: Rad 82:
 
<big>Förkorta bråken så långt som möjligt:</big>
 
<big>Förkorta bråken så långt som möjligt:</big>
  
−
<math> \qquad\quad \displaystyle \frac{2}{4} \quad = \quad \frac{2 \, \color{Red} {/ \, 2}}{4 \, \color{Red} {/ \, 2}} \quad = \quad \frac{1}{2} </math>  
+
<b>1)</b> <math> \quad \displaystyle \frac{2}{4} \; = \; \frac{1 \cdot 2}{2 \cdot 2} \; = \; \frac{1 \cdot \cancel{\color{Red} 2}}{2 \cdot \cancel{\color{Red} 2}} \; = \; \frac{1}{2} </math>  
  
−
<math> \qquad\quad \displaystyle \frac{6}{9} \quad = \quad \frac{6 \, \color{Red} {/ \, 3}}{9 \, \color{Red} {/ \, 3}} \quad = \quad \frac{2}{3} </math>  
+
<b>2)</b> <math> \quad \displaystyle \frac{6}{9} \; = \; \frac{2 \cdot 3}{3 \cdot 3} \; = \; \frac{2 \cdot \cancel{\color{Red} 3}}{3 \cdot \cancel{\color{Red} 3}}  \; = \; \frac{2}{3} </math>
 +
 
 +
<b>3)</b> <math> \quad \displaystyle \frac{10}{15} \; = \; \frac{2 \cdot 5}{3 \cdot 5} \; = \; \; \frac{2 \cdot \cancel{\color{Red} 5}}{3 \cdot \cancel{\color{Red} 5}} \; = \; \frac{2}{3} </math>
 +
 
 +
<b>4)</b> <math> \quad \displaystyle \frac{8}{24} \; = \; \frac{\cancel{\color{Red} 2} \cdot 4}{\cancel{\color{Red} 2} \cdot 12} \, = \, \frac{\cancel{\color{Red} 2} \cdot 2}{\cancel{\color{Red} 2} \cdot 6} \, = \, \frac{\cancel{\color{Red} 2} \cdot 1}{\cancel{\color{Red} 2} \cdot 3} \, = \, \frac{1}{3} </math>
  
 
<b>Metoden:</b>
 
<b>Metoden:</b>
  
−
Hitta ett tal som både täljaren och nämnaren kan
+
Hitta en gemensam [[1.1_Om_tal#Summa_.5C.28-.5C.29_Differens_.5C.28-.5C.29_Produkt_.5C.28-.5C.29_Kvot|<b><span style="color:blue">faktor</span></b>]] hos täljaren och nämna-
  
−
jämnt delas med.
+
ren. <b><span style="color:red">Dividera</span></b> både täljaren och nämnaren med
  
−
<b><span style="color:red">Dividera</span></b> både täljaren och nämnaren med detta tal.
+
samma gemensamma faktor.
 +
</div>
 +
 
 +
 
 +
<big>
 +
<b><span style="color:#931136">Rekommendation:</span></b>
 +
<div class="border-divblue">
 +
Förkorta alltid ett bråk när det är möjligt för att få
  
−
För att hitta talet läs [[1.5_Delbarhet,_primtal_och_faktorisering|<b><span style="color:blue">Delbarhetsreglerna</span></b>]].
+
mindre tal och minska risken för felräknning.  
 
</div>
 
</div>
 +
</big>
  
  
Rad 44: Rad 115:
 
<big>Förläng bråken:</big>
 
<big>Förläng bråken:</big>
  
−
<math> \quad \displaystyle \frac{3}{4} \; = \; \frac{3 {\color{Red} { \, \cdot \, 3}}}{4 {\color{Red} { \, \cdot \, 3}}}  \; = \; \frac{9}{12} </math>  
+
<b>1)</b> <math> \quad \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 3}}{4 \cdot {\color{Red} 3}}  \; = \; \frac{9}{12} </math>  
  
−
<math> \quad \displaystyle \frac{2}{3} \; = \; \frac{2 {\color{Red} { \, \cdot \, 4}}}{3 {\color{Red} { \, \cdot \, 4}}}  \; = \; \frac{8}{12} </math>  
+
<b>2)</b> <math> \quad \displaystyle \frac{2}{3} \; = \; \frac{2 \cdot {\color{Red} 4}}{3 \cdot {\color{Red} 4}}  \; = \; \frac{8}{12} </math>  
  
−
<math> \quad \displaystyle \frac{3}{4} \; = \; \frac{3 {\color{Red} { \, \cdot \, 5}}}{4 {\color{Red} { \, \cdot \, 5}}} \; = \; \frac{15}{20} \; = \; \frac{15 {\color{Red} { \, \cdot \, 5}}}{20 {\color{Red} { \, \cdot \, 5}}} \; = \; \frac{75}{100} </math>
+
<b>3)</b> <math> \quad \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 5}}{4 \cdot {\color{Red} 5}} \; = \; \frac{15}{20} \; = \; \frac{15 \cdot {\color{Red} 5}}{20 \cdot {\color{Red} 5}} \; = \; \frac{75}{100} </math>
 +
 
 +
<b>4)</b> <math> \quad \displaystyle {1 \over 8} \; = \; {1 \cdot {\color{Red} 5} \over 8 \cdot {\color{Red} 5}} \; = \; {5 \over 40} \; = \; {5 \cdot {\color{Red} 5} \over 40 \cdot {\color{Red} 5}} \; = \; {25 \over 200} \; = </math>
 +
 
 +
<math> \qquad\quad\; \displaystyle = \; {25 \cdot {\color{Red} 5} \over 200 \cdot {\color{Red} 5}} \; = \; {125 \over 1\,000} </math>
  
 
<b>Metoden:</b>
 
<b>Metoden:</b>
  
−
<b><span style="color:red">Multiplicera</span></b> täljaren och nämnaren med samma tal
+
<b><span style="color:red">Multiplicera</span></b> täljaren och nämnaren med samma tal.
 +
</div>
 +
 
 +
 
 +
== <b><span style="color:#931136">Varför förlängning?</span></b> ==
 +
<br>
 +
<div class="ovnA">
 +
Exemplen <b>1)</b> och <b>2)</b> visar att bråken genom förläng-
 +
 
 +
ning kan få samma nämnare, vilket gör att man t.ex.
 +
 
 +
kan jämföra dem med varandra<span style="color:black">:</span> <math> \quad\;\; \displaystyle \frac{9}{12} \, > \, \frac{8}{12} </math>
 +
 
 +
och därmed avgöra<span style="color:black">:</span> <math> \qquad\qquad\qquad\; \displaystyle \frac{3}{4} \, > \, \frac{2}{3} </math>
 +
 
 +
Dessutom kam man addera och subtrahera dem.
 +
 
 +
Exemplen <b>3)</b> och <b>4)</b> visar att bråken genom förläng-
 +
 
 +
ning kan få en <math> \, 10</math>-potens i nämnaren, vilket t.ex.
  
−
tills du får önskad nämnare.
+
gör att man direkt kan skriva dem till decimaltal.
 
</div>
 
</div>
 +
 +
 +
<big>
 +
<b><span style="color:#931136">Slutsats:</span></b>
 +
<div class="border-divblue">
 +
Både förkortning och förlängning bibehåller
 +
 +
bråkets <b><span style="color:red">värde</span></b>.
 +
</div>
 +
</big>
  
  
Rad 64: Rad 168:
 
<math> \quad \displaystyle \frac{1}{\color{Red} 5} \; + \; \frac{3}{\color{Red} 5} \; = \; \frac{4}{\color{Red} 5} </math>  
 
<math> \quad \displaystyle \frac{1}{\color{Red} 5} \; + \; \frac{3}{\color{Red} 5} \; = \; \frac{4}{\color{Red} 5} </math>  
  
−
<math> \quad \displaystyle \frac{11}{\color{Red} {12}} \; - \; \frac{5}{\color{Red} {12}} \; = \; \frac{6}{\color{Red} {12}} \; = \; \frac{6 \, / \, 6}{\color{Red} {12} \, / \, 6} \; = \; \frac{1}{2} </math>  
+
<math> \quad \displaystyle \frac{11}{\color{Red} {12}} \; - \; \frac{5}{\color{Red} {12}} \; = \; \frac{6}{\color{Red} {12}} \; = \; \frac{1 \cdot \cancel{6}}{2 \cdot \cancel{6}} \; = \; \frac{1}{2} </math>  
  
 
<math> \quad \displaystyle \frac{5}{\color{Red} {11}} + \frac{13}{\color{Red} {11}} - \frac{9}{\color{Red} {11}} = \frac{5+13-9}{\color{Red} {11}} = \frac{9}{\color{Red} {11}} \quad </math>  
 
<math> \quad \displaystyle \frac{5}{\color{Red} {11}} + \frac{13}{\color{Red} {11}} - \frac{9}{\color{Red} {11}} = \frac{5+13-9}{\color{Red} {11}} = \frac{9}{\color{Red} {11}} \quad </math>  
Rad 104: Rad 208:
 
<b><span style="color:red">sam nämnare</span></b> (oftast nämnarnas produkt).
 
<b><span style="color:red">sam nämnare</span></b> (oftast nämnarnas produkt).
  
−
Använd sedan <b><span style="color:#931136">regeln för add./subtr. av</span></b>
+
Använd <b><span style="color:#931136">regeln för add./subtr. av bråk</span></b>
  
−
<b><span style="color:#931136">bråk med <span style="color:red">lika</span> nämnare (Fall 1)</span></b>.
+
<b><span style="color:#931136">med <span style="color:red">lika</span> nämnare</span></b>.
 
</div>
 
</div>
 
</big>
 
</big>
Rad 118: Rad 222:
 
<math> \quad \displaystyle \frac{2}{3} \; \cdot \; \frac{4}{7} \; = \; \frac{2 \cdot 4}{3 \cdot 7} \; = \; \frac{8}{21} </math>  
 
<math> \quad \displaystyle \frac{2}{3} \; \cdot \; \frac{4}{7} \; = \; \frac{2 \cdot 4}{3 \cdot 7} \; = \; \frac{8}{21} </math>  
  
−
<math> \quad \displaystyle \frac{3}{4} \; \cdot \; \frac{2}{3} \; = \; \frac{3 \cdot 2}{4 \cdot 3} \; = \; \frac{6}{12} \; = \; \frac{6 \, / \, 6}{12 \, / \, 6} \; = \; \frac{1}{2} </math>  
+
<math> \quad \displaystyle \frac{3}{4} \; \cdot \; \frac{2}{3} \; = \; \frac{3 \cdot 2}{4 \cdot 3} \; = \; \frac{6}{12} \; = \; \frac{1 \cdot \cancel{6}}{2 \cdot \cancel{6}} \; = \; \frac{1}{2} </math>  
 
</div>
 
</div>
  
Rad 150: Rad 254:
 
<math> \quad \displaystyle \frac{1}{2} \; \Big/ \; \frac{3}{4} \; = \; \frac{1}{2} \; {\color{Red} {\cdot \; \frac{4}{3}}} \; = \; \frac{1 \cdot 4}{2 \cdot 3} \; = \; \frac{4}{6} \; = \; </math>
 
<math> \quad \displaystyle \frac{1}{2} \; \Big/ \; \frac{3}{4} \; = \; \frac{1}{2} \; {\color{Red} {\cdot \; \frac{4}{3}}} \; = \; \frac{1 \cdot 4}{2 \cdot 3} \; = \; \frac{4}{6} \; = \; </math>
  
−
<math> \qquad\qquad\; \displaystyle \; = \; \frac{4 \, / \, 2}{6 \, / \, 2} \; = \; \frac{2}{3} </math>  
+
<math> \qquad\qquad\; \displaystyle \; = \; \frac{\cancel{2} \cdot 2}{\cancel{2} \cdot 3} \; = \; \frac{2}{3} </math>  
  
 
<math> \quad \displaystyle \frac{2}{3} \; \Big/ \; \frac{5}{7} \; = \; \frac{2}{3} \; {\color{Red} {\cdot \; \frac{7}{5}}} \; = \; \frac{2 \cdot 7}{3 \cdot 5} \; = \; \frac{14}{15} </math>
 
<math> \quad \displaystyle \frac{2}{3} \; \Big/ \; \frac{5}{7} \; = \; \frac{2}{3} \; {\color{Red} {\cdot \; \frac{7}{5}}} \; = \; \frac{2 \cdot 7}{3 \cdot 5} \; = \; \frac{14}{15} </math>
Rad 226: Rad 330:
  
 
<big>
 
<big>
−
<b><span style="color:#931136">Regel för multiplikation av bråk med heltal:</span></b>
+
<b><span style="color:#931136">Regel:</span></b>
 
<div class="border-divblue">
 
<div class="border-divblue">
 
Ta täljaren <math> \times </math> heltalet, bibehåll nämnaren.
 
Ta täljaren <math> \times </math> heltalet, bibehåll nämnaren.
Rad 256: Rad 360:
 
</div>
 
</div>
  
−
 
−
== <b><span style="color:#931136">Tal i blandad form</span></b> ==
 
−
<br>
 
−
<big><math> {\color{Limegreen} {\text{Täljaren}}} \; > \; {\color{red} {\text{nämnaren}}} \; </math><b>:</b></big>
 
−
 
−
<div class="ovnC">
 
−
<div class="exempel"><big>
 
−
<math> \displaystyle \frac{7}{2} \; </math> kan skrivas i <b><span style="color:#931136">blandad form</span></b> <math> \; \displaystyle \boxed{3 \,\frac{1}{2}} \; </math>.
 
−
</big>
 
−
</div>
 
−
 
−
Metoden<span style="color:black">:</span>
 
−
 
−
<math> \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \; \color {Limegreen} 3 \,, {\rm rest} \; 1 \; = \; \boxed{\color {Limegreen} 3 \,\frac{1}{\color {Red} 2}} \quad </math>
 
−
 
−
<math> \quad \color {Red} 2 \; </math> ryms <math> \; \color {Limegreen} 3 \; </math> gånger i <math> \; 7 \; </math> med rest <math> \; 1 \; </math>.
 
−
 
−
Eller med miniräknaren<span style="color:black">:</span>
 
−
 
−
<math> \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \quad\; 3,5 \quad\; = \; \color {Limegreen} 3 \,\frac{1}{\color {Red} 2} \quad </math>
 
−
</div>
 
−
 
−
 
−
 
−
<big>Omvänt:</big>
 
−
 
−
<div class="ovnC">
 
−
<big>Skriv blandade formen till bråk:</big>
 
−
 
−
<math> \quad \displaystyle \boxed{\color {Limegreen} 3\,\frac{1}{\color {Red} 2}} \;\; = \;\; \frac{\color {Limegreen} 3 \, \cdot \color {Red} 2 \quad + \quad 1}{\color {Red} 2} \;\; = \;\; \frac{7}{\color {Red} 2} </math>
 
−
 
−
<math> \;\; </math> Därför att<span style="color:black">:</span>
 
−
 
−
<math> \quad \displaystyle \color {Limegreen} 3\,\frac{1}{\color {Red} 2} \; = \; \color {Limegreen} 3 \; + \; \frac{1}{\color {Red} 2} = \frac{\color {Limegreen} 3}{1} + \frac{1}{\color {Red} 2} \; = </math>
 
−
 
−
<math> \qquad\;\;\, \displaystyle \; = \; \frac{\color {Limegreen} 3 \cdot \color {Red} 2}{1 \cdot \color {Red} 2} \; + \; \frac{1}{\color {Red} 2} \; = \; \frac{6}{\color{Red} 2} \; + \; \frac{1}{\color{Red} 2} \; = \; \frac{7}{\color{Red} 2} </math>
 
−
</div>
 
−
 
−
 
−
<big>
 
−
<b><span style="color:#931136">Slutsats:</span></b>
 
−
<div class="border-divblue">
 
−
I blandade former står mellan heltalet
 
−
 
−
och bråket ett osynligt &nbsp; <big><big><span style="color:red">+</span></big></big> &nbsp; .
 
−
</div>
 
−
</big>
 
−
 
−
 
−
<big>
 
−
<b><span style="color:#931136">Metoden för omvandling av blandad form till bråk:</span></b>
 
−
<div class="border-divblue">
 
−
 
−
<math> \quad \displaystyle \color {Limegreen} a\;\frac{b}{\color {Red} c} \quad = \quad \frac{\color {Limegreen} a \, \cdot \color {Red} c \quad + \quad b}{\color {Red} c} \quad </math>
 
−
</div>
 
−
</big>
 
  
  

Versionen från 8 september 2019 kl. 15.48

        <<  Förra demoavsnitt          Genomgång          Övningar          Nästa demoavsnitt  >>      


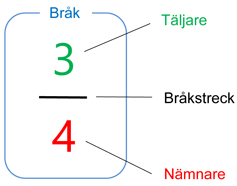
Tal i bråkform


\( \qquad\quad \)

Bild Tal i brakform 30.jpg

Bråkstrecket betyder division:

\( \quad\; \displaystyle \frac{{\color{Limegreen} 3}}{{\color{Red} 4}} \; = \; {\color{Limegreen} 3} \, / \, {\color{Red} 4} \; = \; 0,75 \)

Generellt:

Alla tal i bråkform kan skrivas i decimalform, men inte tvärtom.

T.ex. \( \quad\sqrt{2} = 1,4142135623730950488\ldots \quad \) kan inte anges i bråkform eftersom det har en oändlig icke-periodisk decimalutveckling.

Alla tal som kan skrivas i bråkform kallas för rationella. De som inte kan skrivas i bråkform kallas för irrationella, se Olika typer av tal.


Blandad form


Skriv bråket \( \; \frac{7}{2} \; \) till blandad form:

\( \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \; \color {Limegreen} 3 \,, {\rm rest} \; 1 \; = \; \boxed{\color {Limegreen} 3 \,\frac{1}{\color {Red} 2}} \quad \)

\( \quad \) Eller använd miniräknare:

\( \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \quad\; 3,5 \quad\; = \; \color {Limegreen} 3 \,\frac{1}{\color {Red} 2} \quad \)

OBS!

I blandade former står mellan heltalet och

bråket ett osynligt + :  \( \quad \displaystyle \color {Limegreen} 3 \,\frac{1}{\color {Red} 2} \; = \; \color {Limegreen} 3 \) + \( \displaystyle \frac{1}{\color {Red} 2} \quad \)

Läs därför:                       "Tre och en halv"


Omvänt:

Skriv blandade formen till bråk:

\( \quad \displaystyle \boxed{\color {Limegreen} 3\,\frac{1}{\color {Red} 2}} \;\; = \;\; \frac{\color {Limegreen} 3 \, \cdot \color {Red} 2 \quad + \quad 1}{\color {Red} 2} \;\; = \;\; \frac{7}{\color {Red} 2} \)

\( \quad \) Därför att:

\( \quad \displaystyle \color {Limegreen} 3\,\frac{1}{\color {Red} 2} \; = \; \color {Limegreen} 3 \; + \; \frac{1}{\color {Red} 2} = \frac{\color {Limegreen} 3}{1} + \frac{1}{\color {Red} 2} \; = \)

\( \qquad\;\;\, \displaystyle \; = \; \frac{\color {Limegreen} 3 \cdot \color {Red} 2}{1 \cdot \color {Red} 2} \; + \; \frac{1}{\color {Red} 2} \; = \; \frac{6}{\color{Red} 2} \; + \; \frac{1}{\color{Red} 2} \; = \; \frac{7}{\color{Red} 2} \)


Regeln för att skriva en blandad form till bråk:

\( \quad \displaystyle \color {Limegreen} a\;\frac{b}{\color {Red} c} \quad = \quad \frac{\color {Limegreen} a \, \cdot \color {Red} c \quad + \quad b}{\color {Red} c} \quad \)


Förkortning av bråk


Förkorta bråken så långt som möjligt:

1) \( \quad \displaystyle \frac{2}{4} \; = \; \frac{1 \cdot 2}{2 \cdot 2} \; = \; \frac{1 \cdot \cancel{\color{Red} 2}}{2 \cdot \cancel{\color{Red} 2}} \; = \; \frac{1}{2} \)

2) \( \quad \displaystyle \frac{6}{9} \; = \; \frac{2 \cdot 3}{3 \cdot 3} \; = \; \frac{2 \cdot \cancel{\color{Red} 3}}{3 \cdot \cancel{\color{Red} 3}} \; = \; \frac{2}{3} \)

3) \( \quad \displaystyle \frac{10}{15} \; = \; \frac{2 \cdot 5}{3 \cdot 5} \; = \; \; \frac{2 \cdot \cancel{\color{Red} 5}}{3 \cdot \cancel{\color{Red} 5}} \; = \; \frac{2}{3} \)

4) \( \quad \displaystyle \frac{8}{24} \; = \; \frac{\cancel{\color{Red} 2} \cdot 4}{\cancel{\color{Red} 2} \cdot 12} \, = \, \frac{\cancel{\color{Red} 2} \cdot 2}{\cancel{\color{Red} 2} \cdot 6} \, = \, \frac{\cancel{\color{Red} 2} \cdot 1}{\cancel{\color{Red} 2} \cdot 3} \, = \, \frac{1}{3} \)

Metoden:

Hitta en gemensam faktor hos täljaren och nämna-

ren. Dividera både täljaren och nämnaren med

samma gemensamma faktor.


Rekommendation:

Förkorta alltid ett bråk när det är möjligt för att få

mindre tal och minska risken för felräknning.


Förlängning av bråk


Förläng bråken:

1) \( \quad \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 3}}{4 \cdot {\color{Red} 3}} \; = \; \frac{9}{12} \)

2) \( \quad \displaystyle \frac{2}{3} \; = \; \frac{2 \cdot {\color{Red} 4}}{3 \cdot {\color{Red} 4}} \; = \; \frac{8}{12} \)

3) \( \quad \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 5}}{4 \cdot {\color{Red} 5}} \; = \; \frac{15}{20} \; = \; \frac{15 \cdot {\color{Red} 5}}{20 \cdot {\color{Red} 5}} \; = \; \frac{75}{100} \)

4) \( \quad \displaystyle {1 \over 8} \; = \; {1 \cdot {\color{Red} 5} \over 8 \cdot {\color{Red} 5}} \; = \; {5 \over 40} \; = \; {5 \cdot {\color{Red} 5} \over 40 \cdot {\color{Red} 5}} \; = \; {25 \over 200} \; = \)

\( \qquad\quad\; \displaystyle = \; {25 \cdot {\color{Red} 5} \over 200 \cdot {\color{Red} 5}} \; = \; {125 \over 1\,000} \)

Metoden:

Multiplicera täljaren och nämnaren med samma tal.


Varför förlängning?


Exemplen 1) och 2) visar att bråken genom förläng-

ning kan få samma nämnare, vilket gör att man t.ex.

kan jämföra dem med varandra: \( \quad\;\; \displaystyle \frac{9}{12} \, > \, \frac{8}{12} \)

och därmed avgöra: \( \qquad\qquad\qquad\; \displaystyle \frac{3}{4} \, > \, \frac{2}{3} \)

Dessutom kam man addera och subtrahera dem.

Exemplen 3) och 4) visar att bråken genom förläng-

ning kan få en \( \, 10\)-potens i nämnaren, vilket t.ex.

gör att man direkt kan skriva dem till decimaltal.


Slutsats:

Både förkortning och förlängning bibehåller

bråkets värde.


Addition och subtraktion av bråk


Fall 1   Lika nämnare

\( \quad \displaystyle \frac{1}{\color{Red} 5} \; + \; \frac{3}{\color{Red} 5} \; = \; \frac{4}{\color{Red} 5} \)

\( \quad \displaystyle \frac{11}{\color{Red} {12}} \; - \; \frac{5}{\color{Red} {12}} \; = \; \frac{6}{\color{Red} {12}} \; = \; \frac{1 \cdot \cancel{6}}{2 \cdot \cancel{6}} \; = \; \frac{1}{2} \)

\( \quad \displaystyle \frac{5}{\color{Red} {11}} + \frac{13}{\color{Red} {11}} - \frac{9}{\color{Red} {11}} = \frac{5+13-9}{\color{Red} {11}} = \frac{9}{\color{Red} {11}} \quad \)


Regeln för add./subtr. av bråk med lika nämnare:

Bibehåll och ta över den gemensamma

nämnaren. Addera/subtrahera täljarna.


Fall 2   Olika nämnare

\( \quad \displaystyle \frac{1}{2} \; + \; \frac{1}{3} \; = \; \frac{1 \cdot {\color{Limegreen} 3}}{2 \cdot {\color{Limegreen} 3}} \; + \; \frac{1 \cdot {\color{Limegreen} 2}}{3 \cdot {\color{Limegreen} 2}} \; = \; \)

\( \qquad\qquad\;\; \displaystyle \; = \; \frac{3}{\color{Red} 6} \; + \; \frac{2}{\color{Red} 6} \; = \; \frac{5}{\color{Red} 6} \)

\( \quad \displaystyle \frac{2}{3} \; + \; \frac{1}{5} \; = \; \frac{2 \cdot {\color{Limegreen} 5}}{3 \cdot {\color{Limegreen} 5}} \; + \; \frac{1 \cdot {\color{Limegreen} 3}}{5 \cdot {\color{Limegreen} 3}} \; = \; \)

\( \qquad\qquad\;\; \displaystyle \; = \; \frac{10}{\color{Red} {15}} \; + \; \frac{3}{\color{Red} {15}} \; = \; \frac{13}{\color{Red} {15}} \)

\( \quad \displaystyle \frac{7}{4} \; - \; \frac{5}{3} \; = \; \frac{7 \cdot {\color{Limegreen} 3}}{4 \cdot {\color{Limegreen} 3}} \; - \; \frac{5 \cdot {\color{Limegreen} 4}}{3 \cdot {\color{Limegreen} 4}} \; = \; \)

\( \qquad\qquad\;\; \displaystyle \; = \; \frac{21}{\color{Red} {12}} \; - \; \frac{20}{\color{Red} {12}} \; = \; \frac{1}{\color{Red} {12}} \quad \)


Regeln för add./subtr. av bråk med olika nämnare:

Förläng bråken så att de får en gemen-

sam nämnare (oftast nämnarnas produkt).

Använd regeln för add./subtr. av bråk

med lika nämnare.


Multiplikation av bråk


\( \quad \displaystyle \frac{1}{2} \; \cdot \; \frac{3}{4} \; = \; \frac{1 \cdot 3}{2 \cdot 4} \; = \; \frac{3}{8}\)

\( \quad \displaystyle \frac{2}{3} \; \cdot \; \frac{4}{7} \; = \; \frac{2 \cdot 4}{3 \cdot 7} \; = \; \frac{8}{21} \)

\( \quad \displaystyle \frac{3}{4} \; \cdot \; \frac{2}{3} \; = \; \frac{3 \cdot 2}{4 \cdot 3} \; = \; \frac{6}{12} \; = \; \frac{1 \cdot \cancel{6}}{2 \cdot \cancel{6}} \; = \; \frac{1}{2} \)


Regeln för multiplikation av bråk:

Multiplicera:   täljarna   med   varandra,
  nämnarna   med   varandra.


Allmän regel för redovisning av bråkuppgifter:

Förkorta dina svar så långt som möjligt.


Division av bråk


\( \quad \displaystyle \frac{1}{2} \; \Big/ \; \frac{3}{4} \; = \; \frac{1}{2} \; {\color{Red} {\cdot \; \frac{4}{3}}} \; = \; \frac{1 \cdot 4}{2 \cdot 3} \; = \; \frac{4}{6} \; = \; \)

\( \qquad\qquad\; \displaystyle \; = \; \frac{\cancel{2} \cdot 2}{\cancel{2} \cdot 3} \; = \; \frac{2}{3} \)

\( \quad \displaystyle \frac{2}{3} \; \Big/ \; \frac{5}{7} \; = \; \frac{2}{3} \; {\color{Red} {\cdot \; \frac{7}{5}}} \; = \; \frac{2 \cdot 7}{3 \cdot 5} \; = \; \frac{14}{15} \)

\( \quad \displaystyle \frac{4}{7} \; \Big/ \; \frac{3}{5} \; = \; \frac{4}{7} \; {\color{Red} {\cdot \; \frac{5}{3}}} \; = \; \frac{4 \cdot 5}{7 \cdot 3} \; = \; \frac{20}{21} \)


Regeln för division av bråk:

Ersätt \( / \) med \( {\color{Red} {\cdot}} \) och invertera det bråk som

man skulle dividera med (dvs det andra).

Använd regeln för multiplikation av bråk.

Att invertera t.ex. \( \, \displaystyle \frac{3}{4} \, \) ger \( \, \displaystyle {\color{Red} {\frac{4}{3}}} \; \).


Dubbelbråk


\( \;\; \displaystyle \frac{\frac{{\color{Red} 2}}{{\color{Limegreen} 5}}}{\frac{{\color{Limegreen} 4}}{{\color{Red} 9}}} \) \( \displaystyle \; = \; \frac{{\color{Red} 2} \cdot {\color{Red} 9}}{{\color{Limegreen} 5} \cdot {\color{Limegreen} 4}} \; = \; \frac{\cancel{2} \cdot 9}{5 \cdot 2 \cdot \cancel{2}} \; = \; \frac{9}{5 \cdot 2} \; = \; \frac{9}{10} \)

\( \;\; \) Förkorta även på vägen till svaret om möjligt.


Regeln för dubbelbråk:

Ta de "yttersta" (\( \, {\color{Red} 2} \, \) och \( \, {\color{Red} 9} \, \)) till täljaren.

Ta de "innersta" (\( \, {\color{Limegreen} 5} \, \) och \( \, {\color{Limegreen} 4} \, \)) till nämnaren.


Heltal som bråk


\( \qquad \displaystyle 9 \; = \; \frac{9}{1} \qquad \)


Generellt:

Alla heltal kan skrivas i bråkform

genom att ge dem nämnaren \( \, {\color{Red} 1} \, \).


Bråk gånger heltal


\( \displaystyle \frac{2}{3} \cdot 9 \; = \; \frac{2}{3} \cdot \frac{9}{1} \; = \; \frac{2 \cdot 9}{3 \cdot 1} \; = \; \frac{2 \cdot 3 \cdot \cancel{3}}{\cancel{3}} \; = \; 6 \)

Snabbare:

\( \displaystyle \frac{2}{3} \cdot 9 \; = \; \frac{2 \cdot 9}{3} \; = \; \frac{18}{3} \; = \; 6 \)

\( \displaystyle 2 \cdot \frac{5}{7} \; = \; \frac{2 \cdot 5}{7} \; = \; \frac{10}{7} \)


Regel:

Ta täljaren \( \times \) heltalet, bibehåll nämnaren.


Bråkdel av ett tal


Bestäm \( \; \displaystyle \frac{5}{6} \; \) av \( \; 12 \; \).

\( \quad \displaystyle \frac{5}{6} \; \) \( {\color {Red} {\cdot}} \) \( \; \displaystyle 12 \; = \; \frac{5 \cdot 12}{6} \; = \; \frac{5 \cdot 2 \cdot \cancel{6}}{\cancel{6}} \; = \; 10 \quad \)


Regel:

Översätt av till gånger.


Bestäm \( \; \displaystyle \frac{4}{5} \; \) av \( \; \displaystyle \frac{7}{8} \; \).

\( \quad \displaystyle \frac{4}{5} \; \) \( {\color {Red} {\cdot}} \) \( \; \displaystyle \frac{7}{8} \; = \; \frac{4 \cdot 7}{5 \cdot 8} \; = \; \frac{\cancel{4} \cdot 7}{5 \cdot 2 \cdot \cancel{4}} \; = \; \frac{7}{10} \quad \)




Copyright © 2019 TechPages AB. All Rights Reserved.

Hämtad från "https://minidemo.mathonline.se/index.php?title=1.5_Bråkräkning&oldid=28560"