Skillnad mellan versioner av "1.5 Bråkräkning"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 318: | Rad 318: | ||
| − | [[Matte:Copyrights|Copyright]] © | + | [[Matte:Copyrights|Copyright]] © 2019 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved. |
Versionen från 17 april 2019 kl. 08.51
| << Förra demoavsnitt | Genomgång | Övningar | Nästa demoavsnitt >> |
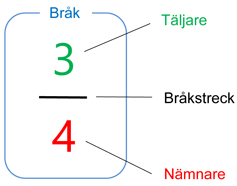
Bråkstrecket betyder division:
\( \quad\; \displaystyle \frac{{\color{Limegreen} 3}}{{\color{Red} 4}} \; = \; {\color{Limegreen} 3} \, / \, {\color{Red} 4} \; = \; 0,75 \)
Förkortning av bråk
Förkorta bråken så långt som möjligt:
\( \qquad\quad \displaystyle \frac{2}{4} \quad = \quad \frac{2 \, \color{Red} {/ \, 2}}{4 \, \color{Red} {/ \, 2}} \quad = \quad \frac{1}{2} \)
\( \qquad\quad \displaystyle \frac{6}{9} \quad = \quad \frac{6 \, \color{Red} {/ \, 3}}{9 \, \color{Red} {/ \, 3}} \quad = \quad \frac{2}{3} \)
Metoden:
Hitta ett tal som både täljaren och nämnaren kan
jämnt delas med.
Dividera både täljaren och nämnaren med detta tal.
För att hitta talet läs Delbarhetsreglerna.
Förlängning av bråk
Förläng bråken:
\( \quad \displaystyle \frac{3}{4} \; = \; \frac{3 {\color{Red} { \, \cdot \, 3}}}{4 {\color{Red} { \, \cdot \, 3}}} \; = \; \frac{9}{12} \)
\( \quad \displaystyle \frac{2}{3} \; = \; \frac{2 {\color{Red} { \, \cdot \, 4}}}{3 {\color{Red} { \, \cdot \, 4}}} \; = \; \frac{8}{12} \)
\( \quad \displaystyle \frac{3}{4} \; = \; \frac{3 {\color{Red} { \, \cdot \, 5}}}{4 {\color{Red} { \, \cdot \, 5}}} \; = \; \frac{15}{20} \; = \; \frac{15 {\color{Red} { \, \cdot \, 5}}}{20 {\color{Red} { \, \cdot \, 5}}} \; = \; \frac{75}{100} \)
Metoden:
Multiplicera täljaren och nämnaren med samma tal
tills du får önskad nämnare.
Addition och subtraktion av bråk
Fall 1 Lika nämnare
\( \quad \displaystyle \frac{1}{\color{Red} 5} \; + \; \frac{3}{\color{Red} 5} \; = \; \frac{4}{\color{Red} 5} \)
\( \quad \displaystyle \frac{11}{\color{Red} {12}} \; - \; \frac{5}{\color{Red} {12}} \; = \; \frac{6}{\color{Red} {12}} \; = \; \frac{6 \, / \, 6}{\color{Red} {12} \, / \, 6} \; = \; \frac{1}{2} \)
\( \quad \displaystyle \frac{5}{\color{Red} {11}} + \frac{13}{\color{Red} {11}} - \frac{9}{\color{Red} {11}} = \frac{5+13-9}{\color{Red} {11}} = \frac{9}{\color{Red} {11}} \quad \)
Regeln för add./subtr. av bråk med lika nämnare:
Bibehåll och ta över den gemensamma
nämnaren. Addera/subtrahera täljarna.
Fall 2 Olika nämnare
\( \quad \displaystyle \frac{1}{2} \; + \; \frac{1}{3} \; = \; \frac{1 \cdot {\color{Limegreen} 3}}{2 \cdot {\color{Limegreen} 3}} \; + \; \frac{1 \cdot {\color{Limegreen} 2}}{3 \cdot {\color{Limegreen} 2}} \; = \; \)
\( \qquad\qquad\;\; \displaystyle \; = \; \frac{3}{\color{Red} 6} \; + \; \frac{2}{\color{Red} 6} \; = \; \frac{5}{\color{Red} 6} \)
\( \quad \displaystyle \frac{2}{3} \; + \; \frac{1}{5} \; = \; \frac{2 \cdot {\color{Limegreen} 5}}{3 \cdot {\color{Limegreen} 5}} \; + \; \frac{1 \cdot {\color{Limegreen} 3}}{5 \cdot {\color{Limegreen} 3}} \; = \; \)
\( \qquad\qquad\;\; \displaystyle \; = \; \frac{10}{\color{Red} {15}} \; + \; \frac{3}{\color{Red} {15}} \; = \; \frac{13}{\color{Red} {15}} \)
\( \quad \displaystyle \frac{7}{4} \; - \; \frac{5}{3} \; = \; \frac{7 \cdot {\color{Limegreen} 3}}{4 \cdot {\color{Limegreen} 3}} \; - \; \frac{5 \cdot {\color{Limegreen} 4}}{3 \cdot {\color{Limegreen} 4}} \; = \; \)
\( \qquad\qquad\;\; \displaystyle \; = \; \frac{21}{\color{Red} {12}} \; - \; \frac{20}{\color{Red} {12}} \; = \; \frac{1}{\color{Red} {12}} \quad \)
Regeln för add./subtr. av bråk med olika nämnare:
Förläng bråken så att de får en gemen-
sam nämnare (oftast nämnarnas produkt).
Använd sedan regeln för add./subtr. av
bråk med lika nämnare (Fall 1).
Multiplikation av bråk
\( \quad \displaystyle \frac{1}{2} \; \cdot \; \frac{3}{4} \; = \; \frac{1 \cdot 3}{2 \cdot 4} \; = \; \frac{3}{8}\)
\( \quad \displaystyle \frac{2}{3} \; \cdot \; \frac{4}{7} \; = \; \frac{2 \cdot 4}{3 \cdot 7} \; = \; \frac{8}{21} \)
\( \quad \displaystyle \frac{3}{4} \; \cdot \; \frac{2}{3} \; = \; \frac{3 \cdot 2}{4 \cdot 3} \; = \; \frac{6}{12} \; = \; \frac{6 \, / \, 6}{12 \, / \, 6} \; = \; \frac{1}{2} \)
Regeln för multiplikation av bråk:
| Multiplicera: | täljarna | med | varandra, |
| nämnarna | med | varandra. |
Allmän regel för redovisning av bråkuppgifter:
Förkorta dina svar så långt som möjligt.
Division av bråk
\( \quad \displaystyle \frac{1}{2} \; \Big/ \; \frac{3}{4} \; = \; \frac{1}{2} \; {\color{Red} {\cdot \; \frac{4}{3}}} \; = \; \frac{1 \cdot 4}{2 \cdot 3} \; = \; \frac{4}{6} \; = \; \)
\( \qquad\qquad\; \displaystyle \; = \; \frac{4 \, / \, 2}{6 \, / \, 2} \; = \; \frac{2}{3} \)
\( \quad \displaystyle \frac{2}{3} \; \Big/ \; \frac{5}{7} \; = \; \frac{2}{3} \; {\color{Red} {\cdot \; \frac{7}{5}}} \; = \; \frac{2 \cdot 7}{3 \cdot 5} \; = \; \frac{14}{15} \)
\( \quad \displaystyle \frac{4}{7} \; \Big/ \; \frac{3}{5} \; = \; \frac{4}{7} \; {\color{Red} {\cdot \; \frac{5}{3}}} \; = \; \frac{4 \cdot 5}{7 \cdot 3} \; = \; \frac{20}{21} \)
Regeln för division av bråk:
Ersätt \( / \) med \( {\color{Red} {\cdot}} \) och invertera det bråk som
man skulle dividera med (dvs det andra).
Använd regeln för multiplikation av bråk.
Att invertera t.ex. \( \, \displaystyle \frac{3}{4} \, \) ger \( \, \displaystyle {\color{Red} {\frac{4}{3}}} \; \).
Dubbelbråk
\( \;\; \displaystyle \frac{\frac{{\color{Red} 2}}{{\color{Limegreen} 5}}}{\frac{{\color{Limegreen} 4}}{{\color{Red} 9}}} \) \( \displaystyle \; = \; \frac{{\color{Red} 2} \cdot {\color{Red} 9}}{{\color{Limegreen} 5} \cdot {\color{Limegreen} 4}} \; = \; \frac{\cancel{2} \cdot 9}{5 \cdot 2 \cdot \cancel{2}} \; = \; \frac{9}{5 \cdot 2} \; = \; \frac{9}{10} \)
\( \;\; \) Förkorta även på vägen till svaret om möjligt.
Regeln för dubbelbråk:
Ta de "yttersta" (\( \, {\color{Red} 2} \, \) och \( \, {\color{Red} 9} \, \)) till täljaren.
Ta de "innersta" (\( \, {\color{Limegreen} 5} \, \) och \( \, {\color{Limegreen} 4} \, \)) till nämnaren.
Heltal som bråk
\( \qquad \displaystyle 9 \; = \; \frac{9}{1} \qquad \)
Generellt:
Alla heltal kan skrivas i bråkform
genom att ge dem nämnaren \( \, {\color{Red} 1} \, \).
Bråk gånger heltal
\( \displaystyle \frac{2}{3} \cdot 9 \; = \; \frac{2}{3} \cdot \frac{9}{1} \; = \; \frac{2 \cdot 9}{3 \cdot 1} \; = \; \frac{2 \cdot 3 \cdot \cancel{3}}{\cancel{3}} \; = \; 6 \)
Snabbare:
\( \displaystyle \frac{2}{3} \cdot 9 \; = \; \frac{2 \cdot 9}{3} \; = \; \frac{18}{3} \; = \; 6 \)
\( \displaystyle 2 \cdot \frac{5}{7} \; = \; \frac{2 \cdot 5}{7} \; = \; \frac{10}{7} \)
Regel för multiplikation av bråk med heltal:
Ta täljaren \( \times \) heltalet, bibehåll nämnaren.
Bråkdel av ett tal
Bestäm \( \; \displaystyle \frac{5}{6} \; \) av \( \; 12 \; \).
\( \quad \displaystyle \frac{5}{6} \; \) \( {\color {Red} {\cdot}} \) \( \; \displaystyle 12 \; = \; \frac{5 \cdot 12}{6} \; = \; \frac{5 \cdot 2 \cdot \cancel{6}}{\cancel{6}} \; = \; 10 \quad \)
Regel:
Översätt av till gånger.
Bestäm \( \; \displaystyle \frac{4}{5} \; \) av \( \; \displaystyle \frac{7}{8} \; \).
\( \quad \displaystyle \frac{4}{5} \; \) \( {\color {Red} {\cdot}} \) \( \; \displaystyle \frac{7}{8} \; = \; \frac{4 \cdot 7}{5 \cdot 8} \; = \; \frac{\cancel{4} \cdot 7}{5 \cdot 2 \cdot \cancel{4}} \; = \; \frac{7}{10} \quad \)
Tal i blandad form
\( {\color{Limegreen} {\text{Täljaren}}} \; > \; {\color{red} {\text{nämnaren}}} \; \):
\( \displaystyle \frac{7}{2} \; \) kan skrivas i blandad form \( \; \displaystyle \boxed{3 \,\frac{1}{2}} \; \).
Metoden:
\( \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \; \color {Limegreen} 3 \,, {\rm rest} \; 1 \; = \; \boxed{\color {Limegreen} 3 \,\frac{1}{\color {Red} 2}} \quad \)
\( \quad \color {Red} 2 \; \) ryms \( \; \color {Limegreen} 3 \; \) gånger i \( \; 7 \; \) med rest \( \; 1 \; \).
Eller med miniräknaren:
\( \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \quad\; 3,5 \quad\; = \; \color {Limegreen} 3 \,\frac{1}{\color {Red} 2} \quad \)
Omvänt:
Skriv blandade formen till bråk:
\( \quad \displaystyle \boxed{\color {Limegreen} 3\,\frac{1}{\color {Red} 2}} \;\; = \;\; \frac{\color {Limegreen} 3 \, \cdot \color {Red} 2 \quad + \quad 1}{\color {Red} 2} \;\; = \;\; \frac{7}{\color {Red} 2} \)
\( \;\; \) Därför att:
\( \quad \displaystyle \color {Limegreen} 3\,\frac{1}{\color {Red} 2} \; = \; \color {Limegreen} 3 \; + \; \frac{1}{\color {Red} 2} = \frac{\color {Limegreen} 3}{1} + \frac{1}{\color {Red} 2} \; = \)
\( \qquad\;\;\, \displaystyle \; = \; \frac{\color {Limegreen} 3 \cdot \color {Red} 2}{1 \cdot \color {Red} 2} \; + \; \frac{1}{\color {Red} 2} \; = \; \frac{6}{\color{Red} 2} \; + \; \frac{1}{\color{Red} 2} \; = \; \frac{7}{\color{Red} 2} \)
Slutsats:
I blandade former står mellan heltalet
och bråket ett osynligt + .
Metoden för omvandling av blandad form till bråk:
\( \quad \displaystyle \color {Limegreen} a\;\frac{b}{\color {Red} c} \quad = \quad \frac{\color {Limegreen} a \, \cdot \color {Red} c \quad + \quad b}{\color {Red} c} \quad \)
Copyright © 2019 TechPages AB. All Rights Reserved.