Skillnad mellan versioner av "1.5 Fördjupning till Kontinuerliga och diskreta funktioner"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 15: | Rad 15: | ||
I genomgången sades att kontinuerlig (motsatsen till diskret) betydde sammanhängande. | I genomgången sades att kontinuerlig (motsatsen till diskret) betydde sammanhängande. | ||
| − | Definitionsmängder till kontinuerliga funktioner är kontinuerliga mängder som t.ex. de rationella eller de reella talen. Som [[1.5_Kontinuerliga_och_diskreta_funktioner#Exempel_2_Kontinuerlig_funktion|< | + | Definitionsmängder till kontinuerliga funktioner är kontinuerliga mängder som t.ex. de rationella eller de reella talen. Som [[1.5_Kontinuerliga_och_diskreta_funktioner#Exempel_2_Kontinuerlig_funktion|<b><span style="color:blue">exempel</span></b>]] på en kontinuerlig funktion ritades grafen till en linjär funktion med en genomdragen rät linje. Kontinuerliga funktioners grafer kan man rita utan att lyfta pennan. Allt detta är fortfarande sant, men alla dessa resonemang är intuitiva. Här följer en mer exakt matematisk definition: |
| − | + | ||
| − | Här följer en mer exakt matematisk definition: | + | |
</div> <!-- tolv1 --> | </div> <!-- tolv1 --> | ||
| − | |||
== <b><span style="color:#931136">Allmän definition för kontinuerliga funktioner</span></b> == | == <b><span style="color:#931136">Allmän definition för kontinuerliga funktioner</span></b> == | ||
| Rad 26: | Rad 23: | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
| − | En funktion <math> \, y = f(x) \, </math> är < | + | En funktion <math> \, y = f(x) \, </math> är <b><span style="color:red">kontinuerlig för</span></b> <math> {\color{Red} {x = a}} \, </math> om: |
::::<math> f(x) \to f(a) \quad {\rm när} \quad x \to a </math> | ::::<math> f(x) \to f(a) \quad {\rm när} \quad x \to a </math> | ||
| Rad 34: | Rad 31: | ||
Läs den andra raden i definitionen så här <math> \; {\rm " }f(x) \, </math> går mot <math> f(a)\, </math> när <math> x\, </math> går mot <math> a \, {\rm "} </math>. | Läs den andra raden i definitionen så här <math> \; {\rm " }f(x) \, </math> går mot <math> f(a)\, </math> när <math> x\, </math> går mot <math> a \, {\rm "} </math>. | ||
| − | Observera att definitionen är punktvis, dvs den talar om när en funktion är kontinuerlig < | + | Observera att definitionen är punktvis, dvs den talar om när en funktion är kontinuerlig <b><span style="color:red">för ett visst</span></b> <math> {\color{Red} x}\, </math><b><span style="color:red">-värde</span></b> nämligen för <math> {\color{Red} {x = a}}\, </math>. |
Man skulle kunna lägga till att en funktion i sin helhet är kontinuerlig om den är kontinuerlig för alla <math> \, x\, </math>. Då måste även kontinuitet prövas för varje <math> \, x\, </math>. | Man skulle kunna lägga till att en funktion i sin helhet är kontinuerlig om den är kontinuerlig för alla <math> \, x\, </math>. Då måste även kontinuitet prövas för varje <math> \, x\, </math>. | ||
| Rad 40: | Rad 37: | ||
| − | <div class=" | + | <div class="ovnC"> |
==== <b><span style="color:#931136">Exempel 1</span></b> ==== | ==== <b><span style="color:#931136">Exempel 1</span></b> ==== | ||
| Rad 49: | Rad 46: | ||
<div class="exempel"> | <div class="exempel"> | ||
| − | < | + | <b><span style="color:#931136">a)</span></b> Är denna funktion enligt definition kontinuerlig för <math> {\color{Red} {x = 1}}\, </math>? |
I definitionen ersätter vi <big><math> \, {\color{Red} a} \, </math></big> med <math> \, {\color{Red} 1} </math> och <math> \, f(x) \, </math> med <math> \displaystyle{5 \over x \, - \, 1}</math>. | I definitionen ersätter vi <big><math> \, {\color{Red} a} \, </math></big> med <math> \, {\color{Red} 1} </math> och <math> \, f(x) \, </math> med <math> \displaystyle{5 \over x \, - \, 1}</math>. | ||
| Rad 59: | Rad 56: | ||
Dvs <math> \, f(1) = \displaystyle{5 \over 1 \, - \, 1} </math> är inte ens definierad. Så, <math> \, f(x) = \displaystyle{5 \over x \, - \, 1} \, </math> kan inte gå mot något som inte är definierat. Därmed är definitionens krav inte uppfyllt. | Dvs <math> \, f(1) = \displaystyle{5 \over 1 \, - \, 1} </math> är inte ens definierad. Så, <math> \, f(x) = \displaystyle{5 \over x \, - \, 1} \, </math> kan inte gå mot något som inte är definierat. Därmed är definitionens krav inte uppfyllt. | ||
| − | < | + | <b><span style="color:#931136">Slutsats:</span></b> Funktionen <math> \, y = \displaystyle{5 \over x \, - \, 1} \, </math> är inte kontinuerlig för <math> \, x = 1 </math>. |
</div> | </div> | ||
| Rad 69: | Rad 66: | ||
<div class="exempel"> | <div class="exempel"> | ||
| − | < | + | <b><span style="color:#931136">b)</span></b> Är samma funktion enligt definition kontinuerlig för <math> {\color{Red} {x = 2}}\, </math>? |
I definitionen ersätter vi <big><math> \, {\color{Red} a} \, </math></big> med <math> \, {\color{Red} 2} </math> och <math> \, f(x) \, </math> med <math> \displaystyle{5 \over x \, - \, 1}</math>. | I definitionen ersätter vi <big><math> \, {\color{Red} a} \, </math></big> med <math> \, {\color{Red} 2} </math> och <math> \, f(x) \, </math> med <math> \displaystyle{5 \over x \, - \, 1}</math>. | ||
| Rad 77: | Rad 74: | ||
Vi kontrollerar detta i funktionsuttrycket: Låter vi <math> \, x \, </math> gå mot <math> \, 2 \, </math>, går <math> \, y \, </math> mot värdet <math> \, 5 </math>, och slutligen är <math> \, f(2) = 5 </math>. Därmed är dfinitionens krav uppfyllt. | Vi kontrollerar detta i funktionsuttrycket: Låter vi <math> \, x \, </math> gå mot <math> \, 2 \, </math>, går <math> \, y \, </math> mot värdet <math> \, 5 </math>, och slutligen är <math> \, f(2) = 5 </math>. Därmed är dfinitionens krav uppfyllt. | ||
| − | < | + | <b><span style="color:#931136">Slutsats:</span></b> Funktionen <math> \, y = \displaystyle{5 \over x \, - \, 1} \, </math> är kontinuerlig för <math> x = 2\, </math>. |
</div> | </div> | ||
| Rad 95: | Rad 92: | ||
Resultatet kan också ses i grafen: Endast i <math> \, x \, = \, 1 \, </math> skenar kurvorna iväg mot oändligheten, den ena mot <math> \, + \infty\, </math>, den andra mot <math> \, - \infty\, </math>, annars är de sammanhängande. | Resultatet kan också ses i grafen: Endast i <math> \, x \, = \, 1 \, </math> skenar kurvorna iväg mot oändligheten, den ena mot <math> \, + \infty\, </math>, den andra mot <math> \, - \infty\, </math>, annars är de sammanhängande. | ||
| − | </div> <!-- | + | </div> <!-- ovnE Exempel 1 --> |
| − | <div class=" | + | <div class="ovnC"> |
==== <b><span style="color:#931136">Exempel 2</span></b> ==== | ==== <b><span style="color:#931136">Exempel 2</span></b> ==== | ||
| − | Inom datateknik används en funktion som heter [http://sv.wikipedia.org/wiki/Heavisides_stegfunktion < | + | Inom datateknik används en funktion som heter [http://sv.wikipedia.org/wiki/Heavisides_stegfunktion <b><span style="color:blue">Heavisidefunktionen</span></b>]. Funktionens skapare [http://sv.wikipedia.org/wiki/Oliver_Heaviside <b><span style="color:blue">Oliver Heaviside</span></b>] använde den för att modellera strömmen genom elektriska kretsar. Så här definieras funktionen: |
<div class="border-div"><math> y \, = \, H(x) \, = \, \begin{cases} -1 & \mbox{om } x < 0 \\ | <div class="border-div"><math> y \, = \, H(x) \, = \, \begin{cases} -1 & \mbox{om } x < 0 \\ | ||
| Rad 131: | Rad 128: | ||
<div class="exempel"> | <div class="exempel"> | ||
| − | Låt oss nu med hjälp av den [[1.5_Fördjupning_till_Kontinuerliga_och_diskreta_funktioner#Allm.C3.A4n_definition|< | + | Låt oss nu med hjälp av den [[1.5_Fördjupning_till_Kontinuerliga_och_diskreta_funktioner#Allm.C3.A4n_definition|<b><span style="color:blue">allmänna definitionen</span></b>]] för kontinuerliga funktioner undersöka om Heavisidefunktionen är kontinuerlig för <math> \, {\color{Red} {x = 0}} </math>. |
Enligt definitionen borde då <math> \; H(x) \to H(0) \quad {\rm när} \quad x \to 0 </math>. | Enligt definitionen borde då <math> \; H(x) \to H(0) \quad {\rm när} \quad x \to 0 </math>. | ||
| Rad 174: | Rad 171: | ||
<div class="tolv"> <!-- tolv4 --> | <div class="tolv"> <!-- tolv4 --> | ||
| − | I [[1.5_Fördjupning_till_Kontinuerliga_och_diskreta_funktioner#Exempel_1|< | + | I [[1.5_Fördjupning_till_Kontinuerliga_och_diskreta_funktioner#Exempel_1|<b><span style="color:blue">Exempel 1</span></b>]] är funktionen inte kontinuerlig för <math> \, x = 1 \, </math> därför att <math> \, \displaystyle{y = {5 \over x \, - \, 1}} \, </math> överhuvudtaget inte är definierad för <math> x = 1\, </math>. Kurvorna skenar iväg mot oändligheten, den ena mot <math> \, + \infty \, </math>, den andra mot <math> \, - \infty </math>. Detta beror förstås på funktionsuttrycket som inte är definierad för <math> \, x = 1 </math>. Vi har ett slags <b><span style="color:red">oändlighetsställe</span></b> i <math> x = 1\, </math> vilket är ganska typiskt för rationella funktioner. Den här typen av diskontinuitet är en konsekvens av funktionens icke-definierbarhet i <math> \, x = 1\, </math>. Annars är funktionen kontinuerlig i sin definitionsmängd. |
</div class="tolv"> <!-- tolv3 --> | </div class="tolv"> <!-- tolv3 --> | ||
| Rad 181: | Rad 178: | ||
<div class="tolv"> <!-- tolv4 --> | <div class="tolv"> <!-- tolv4 --> | ||
| − | I [[1.5_Fördjupning_till_Kontinuerliga_och_diskreta_funktioner#Exempel_2|< | + | I [[1.5_Fördjupning_till_Kontinuerliga_och_diskreta_funktioner#Exempel_2|<b><span style="color:blue">Exempel 2</span></b>]] är Heavisidefunktionen inte kontinuerlig för <math> \, x = 0\, </math> därför att <math> \, H(x) \, </math> har ett <b><span style="color:red">hopp</span></b> i sitt förlopp just i <math> \, x = 0 </math>. Den har ett väl definierat värde för <math> \, x = 0 </math>, nämligen <math> \, H(0) = 0 </math>. Men hoppet från <math> \, -1 \, </math> till <math> \, 0 \, </math> och vidare från <math> \, 0 \, </math> till <math> \, 1 \, </math> gör att det uppstår en diskontinuitet just där. Att denna diskontinuitet är av en annan typ än oändlighetsstället i [[1.5_Fördjupning_till_Kontinuerliga_och_diskreta_funktioner#Exempel_1|<b><span style="color:blue">Exempel 1</span></b>]] är uppenbart. Till skillnad från Exempel 1 är funktionen i alla fall beräknebar, trots diskontinuiteten. Ja, den är t.o.m en bra modell för verkligheten, för så beter sig en signal när den hoppar från noll till ett, nämligen diskontinuerligt. |
| − | Det finns även andra typer av diskontinuitet, men < | + | Det finns även andra typer av diskontinuitet, men <b><span style="color:red">oändlighetsställe</span></b> och <b><span style="color:red">hopp</span></b> är de oftast förekommande hos kontinuerliga funktioner. |
</div class="tolv"> <!-- tolv5 --> | </div class="tolv"> <!-- tolv5 --> | ||
Versionen från 1 oktober 2016 kl. 21.44
| \( \pmb{\gets} \) Förra demoavsnitt | Genomgång | Övningar | Fördjupning | Nästa demoavsnitt \( \pmb{\to} \) |
Lektion 9 Kontinuerliga & diskreta funktioner
I genomgången sades att kontinuerlig (motsatsen till diskret) betydde sammanhängande.
Definitionsmängder till kontinuerliga funktioner är kontinuerliga mängder som t.ex. de rationella eller de reella talen. Som exempel på en kontinuerlig funktion ritades grafen till en linjär funktion med en genomdragen rät linje. Kontinuerliga funktioners grafer kan man rita utan att lyfta pennan. Allt detta är fortfarande sant, men alla dessa resonemang är intuitiva. Här följer en mer exakt matematisk definition:
Allmän definition för kontinuerliga funktioner
En funktion \( \, y = f(x) \, \) är kontinuerlig för \( {\color{Red} {x = a}} \, \) om:
- \[ f(x) \to f(a) \quad {\rm när} \quad x \to a \]
Läs den andra raden i definitionen så här \( \; {\rm " }f(x) \, \) går mot \( f(a)\, \) när \( x\, \) går mot \( a \, {\rm "} \).
Observera att definitionen är punktvis, dvs den talar om när en funktion är kontinuerlig för ett visst \( {\color{Red} x}\, \)-värde nämligen för \( {\color{Red} {x = a}}\, \).
Man skulle kunna lägga till att en funktion i sin helhet är kontinuerlig om den är kontinuerlig för alla \( \, x\, \). Då måste även kontinuitet prövas för varje \( \, x\, \).
Exempel 1
Låt oss titta på följande rationell funktion:
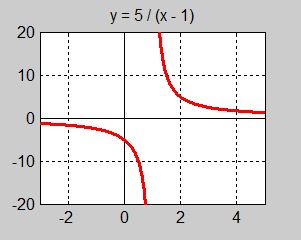
a) Är denna funktion enligt definition kontinuerlig för \( {\color{Red} {x = 1}}\, \)?
I definitionen ersätter vi \( \, {\color{Red} a} \, \) med \( \, {\color{Red} 1} \) och \( \, f(x) \, \) med \( \displaystyle{5 \over x \, - \, 1}\).
Definitionen säger: \( \, f(x) = \displaystyle{5 \over x \, - \, 1} \, \) är kontinuerlig för \( \, {\color{Red} {x = 1}}\, \) om \( \, \displaystyle{5 \over x \, - \, 1} \to f(1) \quad {\rm när} \quad x \to 1 \).
Vi kontrollerar detta både i funktionsuttrycket och i grafen: Låter vi \( \, x \, \) gå mot \( \, 1 \, \), går \( \, y\, \) mot \( +\infty \) eller \( -\infty \).
Dvs \( \, f(1) = \displaystyle{5 \over 1 \, - \, 1} \) är inte ens definierad. Så, \( \, f(x) = \displaystyle{5 \over x \, - \, 1} \, \) kan inte gå mot något som inte är definierat. Därmed är definitionens krav inte uppfyllt.
Slutsats: Funktionen \( \, y = \displaystyle{5 \over x \, - \, 1} \, \) är inte kontinuerlig för \( \, x = 1 \).
Exemplet visar att en funktion måste åtminstone vara definierad för ett visst \( \, x \), för att den ska vara kontinuerlig för detta \( \, x \).
Att vara definierad är en förutsättning för att en funktion ska vara kontinuerlig.
b) Är samma funktion enligt definition kontinuerlig för \( {\color{Red} {x = 2}}\, \)?
I definitionen ersätter vi \( \, {\color{Red} a} \, \) med \( \, {\color{Red} 2} \) och \( \, f(x) \, \) med \( \displaystyle{5 \over x \, - \, 1}\).
Definitionen säger: \( \, f(x) = \displaystyle{5 \over x \, - \, 1} \, \) är kontinuerlig för \( \, {\color{Red} {x = 2}}\, \) om \( \, \displaystyle{5 \over x \, - \, 1} \to f(2) = \displaystyle{5 \over 2 \, - \, 1} = 5 \quad {\rm när} \quad x \to 2 \).
Vi kontrollerar detta i funktionsuttrycket: Låter vi \( \, x \, \) gå mot \( \, 2 \, \), går \( \, y \, \) mot värdet \( \, 5 \), och slutligen är \( \, f(2) = 5 \). Därmed är dfinitionens krav uppfyllt.
Slutsats: Funktionen \( \, y = \displaystyle{5 \over x \, - \, 1} \, \) är kontinuerlig för \( x = 2\, \).
På samma sätt kan man undersöka om funktionen är kontinuerlig för andra \( \, x \). Sammanfattningsvis blir resultatet:
Resultatet kan också ses i grafen: Endast i \( \, x \, = \, 1 \, \) skenar kurvorna iväg mot oändligheten, den ena mot \( \, + \infty\, \), den andra mot \( \, - \infty\, \), annars är de sammanhängande.
Exempel 2
Inom datateknik används en funktion som heter Heavisidefunktionen. Funktionens skapare Oliver Heaviside använde den för att modellera strömmen genom elektriska kretsar. Så här definieras funktionen:
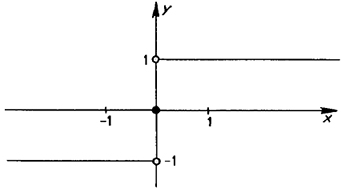
De ihåliga ringarna i grafen vid \( \, y = 1 \, \) och \( \, y = -1 \, \) betyder att dessa värden inte tillhör funktionens värdemängd, dvs \( \, H(0) \, \neq \, 1 \, \) och \( \, H(0) \, \neq \, -1 \).
Den ifyllda ringen vid origo innebär att detta värde tillhör värdemängden, dvs \( \, H(0) \, = \, 0 \).
Grafen visar en signal vars amplitud skiftar från 0 till 1 \(-\) en egenskap som liknar impulserna inom datornätverk med ettor och nollor.
Precis som hos Fibonaccis funktion har man definierat en och samma funktion med olika funktionsuttryck i olika delar av dess definitionsmängd.
Kanske kan formeln ovan samt grafen, inkl. de ihåliga och ifyllda ringarna, förstås bättre med följande förenkling (OBS! Matematiskt inte korrekt):
- \[\begin{array}{rcl} H(\mbox{negativa}\; x) & = & -1 \\ H(0) & = & 0 \\ H(\mbox{positiva}\; x) & = & 1 \end{array}\]
Dvs \( \, H(x) \, \) har för negativa \( \, x \, \) värdet \( \, -1 \, \), för \( \, x = 0 \, \) värdet \( \, 0 \, \) och för positiva \( \, x \, \) värdet \( \, 1 \, \).
Låt oss nu med hjälp av den allmänna definitionen för kontinuerliga funktioner undersöka om Heavisidefunktionen är kontinuerlig för \( \, {\color{Red} {x = 0}} \).
Enligt definitionen borde då \( \; H(x) \to H(0) \quad {\rm när} \quad x \to 0 \).
Närmar man sig \( \, 0 \, \) på \( \, x\)-axeln från höger närmar sig \( \, H(x) \, \) värdet \( \, 1 \).
Närmar man sig \( \, 0 \, \) från vänster närmar sig \( \, H(x) \, \) värdet \( \, -1 \).
Dvs \( \, H(x) \to 1 \, \) och \( \to -1\, \) när \( \, x \to 0 \).
Men \( \, H(0) = 0 \, \). \( \, H(x) \, \) går dock inte mot \( \, H(0) = 0 \, \) när \( \, x \to 0 \), vilket den borde göra om den hade varit kontinuerlig för \( \, x = 0 \).
Därmed är definitionens krav inte uppfyllt. Funktionen \( \, H(x) \, \) är inte kontinuerlig för \( \, x = 0 \).
Undersökar man vidare kontinuiteten för andra \( x\, \) kommer det att visa sig att \( H(x)\, \) är kontinuerlig för alla andra \( x\, \):
Resultatet kan också ses i grafen: Endast i \( \, x=0 \, \) har den ett hopp, annars är den sammanhängande.
Olika typer av diskontinuitet
Jämför man Exempel 1 med Exempel 2 kan man konstatera: Båda funktionerna är kontinuerliga för alla \( \, x \, \) förutom för en isolerad punkt. Men funktionernas definition \(-\) och även graferna \(-\) visar ändå en ganska markant skillnad. Faktiskt handlar det om två helt olika typer av diskontinuitet i de isolerade punkterna:
Diskontinuitet av typ oändlighetsställe
I Exempel 1 är funktionen inte kontinuerlig för \( \, x = 1 \, \) därför att \( \, \displaystyle{y = {5 \over x \, - \, 1}} \, \) överhuvudtaget inte är definierad för \( x = 1\, \). Kurvorna skenar iväg mot oändligheten, den ena mot \( \, + \infty \, \), den andra mot \( \, - \infty \). Detta beror förstås på funktionsuttrycket som inte är definierad för \( \, x = 1 \). Vi har ett slags oändlighetsställe i \( x = 1\, \) vilket är ganska typiskt för rationella funktioner. Den här typen av diskontinuitet är en konsekvens av funktionens icke-definierbarhet i \( \, x = 1\, \). Annars är funktionen kontinuerlig i sin definitionsmängd.
Diskontinuitet av typ hopp
I Exempel 2 är Heavisidefunktionen inte kontinuerlig för \( \, x = 0\, \) därför att \( \, H(x) \, \) har ett hopp i sitt förlopp just i \( \, x = 0 \). Den har ett väl definierat värde för \( \, x = 0 \), nämligen \( \, H(0) = 0 \). Men hoppet från \( \, -1 \, \) till \( \, 0 \, \) och vidare från \( \, 0 \, \) till \( \, 1 \, \) gör att det uppstår en diskontinuitet just där. Att denna diskontinuitet är av en annan typ än oändlighetsstället i Exempel 1 är uppenbart. Till skillnad från Exempel 1 är funktionen i alla fall beräknebar, trots diskontinuiteten. Ja, den är t.o.m en bra modell för verkligheten, för så beter sig en signal när den hoppar från noll till ett, nämligen diskontinuerligt.
Det finns även andra typer av diskontinuitet, men oändlighetsställe och hopp är de oftast förekommande hos kontinuerliga funktioner.
Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.