Skillnad mellan versioner av "1.3 Decimaltal"
Taifun (Diskussion | bidrag) (Skapade sidan med '{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | style="border-bottom:1px solid #797979" width="5px" | {{Not selected tab|1.2 Räkneordning| <...') |
(Ingen skillnad)
|
Versionen från 19 oktober 2015 kl. 10.51
| <-- Förra avsnitt | Genomgång | Avrundning & värdesiffror | Övningar | Nästa avsnitt --> |
Tal mellan två heltal
Decimaltal \(-\) eller tal i decimalform \(-\) är tal som ligger mellan två heltal.
För att visa decimaltal fortsätter man med det decimala positionssystemet.
Heltalens framställning i det decimala positionssystemet förklarades i avsnittet Om tal, Exempel 1.
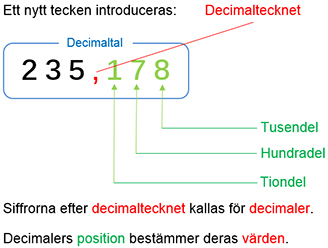
Till heltalsdelen \( 235\):s lägger man till några bråkdelar av \( \, 1 \, \) efter decimaltecknet, närmare bestämt decimalerna \( \, \ldots{\bf{\color{Red},}}{\color{LimeGreen} {178}} \, \).
På så sätt hamnar decimaltalets värde mellan heltalen \( \, 235 \, \) och \( \, 236 \).
Exempel 1
Bestäm decimalernas värden i decimaltalet \( \, 235{\bf{\color{Red},}}{\color{LimeGreen} {178}} \, \). Beräkna decimaltalets värde utgående från decimalernas värden.
Lösning:
- Första decimalen \( \, {\color{LimeGreen} 1} \, \) är en tiondelssiffra och har därmed värdet \( \, {\color{LimeGreen} 1} \cdot 0,1 \;\;\;\; = \, {\color{Red}{0,1}} \, \).
- Andra decimalen \( \, {\color{LimeGreen} 7} \, \) är en hundradelssiffra och har därmed värdet \( \, {\color{LimeGreen} 7} \cdot 0,01 \;\; = \, {\color{Red}{0,07}} \, \).
- Tredje decimalen \( \, {\color{LimeGreen} 8} \, \) är en tusendelssiffra och har därmed värdet \( \, {\color{LimeGreen} 8} \cdot 0,001 \, = \, {\color{Red}{0,008}} \, \).
Summerar man alla decimalers värden beräknas decimaltalets värde till:
- \[ 235 \quad {\bf+} \quad {\color{Red}{0,1 \, + \, 0,07 \, + \, 0,008}} \quad = \quad 235\,{\bf{\color{Red},}}\,{\color{LimeGreen} {178}} \]
Samma regel som gällde för heltal, gäller för decimaltal, fast lite annorlunda formulerad:
I det decimala positionssystemet har varje position ett \( \, 10 \, \) gånger mindre värde än positionen till vänster.
Praktiska slutsatser ur denna regel:
Exempel 2
- \[ 235\,{\bf{\color{Red},}}\,178 \, \cdot \, 0,1 \, = \, 23\,{\bf{\color{Red},}}\,5178 \]
- \[ 235\,{\bf{\color{Red},}}\,178 \, \cdot \, 0,01 \, = \, 2\,{\bf{\color{Red},}}\,35178 \]
- \[ 235\,{\bf{\color{Red},}}\,178 \, \cdot \, 0,001 \, = \, 0\,{\bf{\color{Red},}}\,235\,178 \]
Att multiplicera med \( \, 0,1 \, \) innebär att förminska med faktorn \( \, 10 \, \) dvs att flytta decimaltecknet \( \, 1 \, \) position till vänster.
Att multiplicera med \( \, 0,01 \, \) innebär att förminska med faktorn \( \, 100 \, \) dvs att flytta decimaltecknet \( \, 2 \, \)positioner till vänster.
Att multiplicera med \( \, 0,001 \, \) innebäratt förminska med faktorn \( \, 1\,000 \, \) dvs att flytta decimaltecknet \( \, 3 \, \)positioner till vänster.
Kan ett heltal vara decimaltal?
Om decimaltal ligger mellan två heltal, hur ligger det till med heltalen själva?
Exempel 3
Är \( \, 7\,142 \, \) ett heltal eller ett decimaltal? Motivera.
Svar:
- \( \, 7\,142 \, \) är både heltal och decimaltal.
- Heltal, därför att det inte finns något decimaltecken i det.
- Decimaltal, därför att man kan sätta ett decimaltecken och skriva: \( \qquad 7\,142 \; = \; 7\,142 \, {\bf{\color{Red},}} \, {\color{LimeGreen} {000\, \ldots}} \)
Detta är bara ett exempel på följande generell egenskap:
Alla heltal är decimaltal, men inte tvärtom.
Praktiskt taget kan man tillfoga till alla heltal ett decimaltecken följt av nollor, så att man ser att heltalet också är decimaltal. Ett annat sätt att uttrycka det är att betrakta talen som mängder:
Mängden av alla heltal är en delmängd av alla decimaltal, se bilden i Olika typer av tal, där decimaltal \( \, = \, \) rationella & reella tal.
En praktisk konsekvens av Exempel 3 är följande regel:
Alla nollor efter decimaltecknet kan utelämnas, om ingen siffra \( \neq 0 \, \) följer efter nollorna.
Placering av decimaltal på tallinjen
Kunskapen om decimaltalens värde ska hjälpa oss att ha en uppfattning om decimaltalens storlek och deras korrekta placering på tallinjen.
Exempel 4
Vilket decimaltal pekar pilen på? \(\quad \) 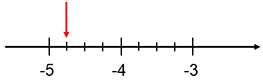
Lösning:
Förklaring:
- Vi befinner oss på den negativa delen av tallinjen.
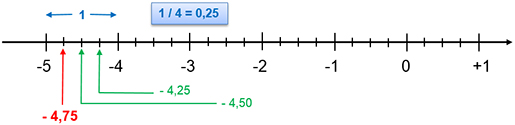
- Skalans minsta steg på tallinjen är: \( \; 1 \,/\, 4 \, = \, \displaystyle{{1 \over 4} \, = \, {1 \cdot {\color{Red} 5} \over 4 \cdot {\color{Red} 5}} \, = \, {5 \over 20} \, = \, {5 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \, = \, {25 \over 100}} \, = \, 0,25 \)
- Det sökta decimaltalet ligger mellan heltalen \( \, -4 \, \) och \( \, -5 \).
- Utgående från \( \, -4 \, \) rör vi oss tre steg till vänster för att hitta det sökta decimaltalet: \( \, -4 \,-\, 0,25 \,-\, 0,25 \,-\, 0,25 \, = \, {\color{Red} {-4,75}}\).
Omvandlingen av \( \, 1 \,/\, 4 \, \) till \( \, 0,25 \, \) i förklaringen ovan är ett exempel på användningen av viktiga decimaltal. Här sammanfattas några:
Viktiga decimaltal
|
|
|
|
I exemplen ovan kan man skilja åt tre grupper: decimaltal med s.k.
- ändlig decimalutveckling, t.ex. \( \, 0,75 \, \) och alla decimaltal i de två första kolumnerna ovan.
- periodisk decimalutveckling, t.ex. \( \, 333\,333\,\ldots \, \) och alla decimaltal i den tredje kolumnen.
- icke-periodisk decimalutveckling, t.ex. \( \, \pi \, = \, 3,141592653589793\,\ldots \, \) och alla decimaltal i den fjärde kolumnen.
De två första grupperna bildar de rationella talen, medan den tredje gruppen tillhör de reella talen, se Olika typer av tal.
Alla ändliga och periodiska decimalutvecklingar kan man skriva i bråkform (rationella), medan det inte längre går med de icke-periodiska (reella).
Ändlig decimalutveckling
Så kallas decimaltal med ändligt många decimaler \(-\) den vanligaste typen av decimaltal \(-\) om man följer den redan nämnda regeln att utelämna nollorna efter decimaltecknet, t.ex. \( \,0,75\,000\,000\,\ldots \, = \, 0,75 \, \).
Ändliga decimalutvecklingar kan alltid skrivas om till bråk. Omvänt kan bråk alltid skrivas om till ändliga eller periodiska decimalutvecklingar.
För att skriva decimaltal till bråk skrivs decimaltalet som ett bråk med en \( \, 10\)-potens (\( \, 1 \, \) med nollor) i nämnaren och förkortas så långt som möjligt:
Exempel 5
a) Skriv \( \; 0,75 \; \) i bråkform.
Lösning: \( \; 0,75 \, = \, \displaystyle{{75 \over 100} \, = \, {15 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \, = \, {3 \cdot {\color{Red} {5 \cdot 5}} \over 4 \cdot {\color{Red} {5 \cdot 5}}} \, = \, {3 \cdot \cancel{\color{Red} {5 \cdot 5}} \over 4 \cdot \cancel{\color{Red} {5 \cdot 5}}} \, = \, {3 \over 4} } \)
b) Skriv \( \; 0,125 \; \) i bråkform.
Lösning: \( \; 0,125 \, = \, \displaystyle{{125 \over 1000} \, = \, {25 \cdot {\color{Red} 5} \over 200 \cdot {\color{Red} 5}} \, = \, {5 \cdot {\color{Red} {5 \cdot 5}} \over 40 \cdot {\color{Red} {5 \cdot 5}}} \, = \, {1 \cdot {\color{Red} {5 \cdot 5 \cdot 5}} \over 8 \cdot {\color{Red} {5 \cdot 5 \cdot 5}}} \, = \, {1 \cdot \cancel{\color{Red} {5 \cdot 5 \cdot 5}} \over 8 \cdot \cancel{\color{Red} {5 \cdot 5 \cdot 5}}} \, = \, {1 \over 8} } \)
Omvänt: För att skriva bråk till decimaltal förlängs bråket med målet att åstadkomma en \( \, 10\)-potens (\( \, 1 \, \) med nollor) i nämnaren. Är detta möjligt kan ändlig decimalutveckling uppnås. Annars är endast periodisk decimalutveckling möjlig som kan åstadkommas med metoder liknande Exempel 7.
Exempel 6
a) Skriv \( \; \displaystyle{3 \over 4} \; \) till decimaltal.
Lösning: \( \; \displaystyle{{3 \over 4} \, = \, {3 \cdot {\color{Red} 5} \over 4 \cdot {\color{Red} 5}} \, = \, {15 \over 20} \, = \, {15 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \, = \, {75 \over 100}} \, = \, 0,75 \)
b) Skriv \( \; \displaystyle{1 \over 8} \; \) till decimaltal.
Lösning: \( \; \displaystyle{{1 \over 8} \, = \, {1 \cdot {\color{Red} 5} \over 8 \cdot {\color{Red} 5}} \, = \, {5 \over 40} \, = \, {5 \cdot {\color{Red} 5} \over 40 \cdot {\color{Red} 5}} \, = \, {25 \cdot {\color{Red} 5} \over 200 \cdot {\color{Red} 5}} \, = \, {125 \over 1000}} \, = \, 0,125 \)
Periodisk decimalutveckling
Så kallas decimaltal med oändligt många decimaler där decimalerna upprepas enligt ett mönster antingen som en enskild siffra eller gruppvis. Mönstret kallas för period. T.ex. har den periodiska decimalutvecklingen \( \, 0,333\,333\,\ldots \, \) perioden \( \, 3 \, \), medan \( \, 0,363636 \ldots \, \) har perioden \( \, 36 \, \).
Periodiska decimalutvecklingar kan inte skrivas om till bråk med en \( \, 10\)-potens i nämnaren, därför att de har oändligt många decimaler. Deras nämnare kan därför inte vara en \( \, 10\)-potens. Andra hjälpmedel än för ändliga decimalutvecklingar måste användas för att åstadkomma denna omskrivning:
Exempel 7
a) Skriv \( \; 0,333\,333\,\ldots \; \) i bråkform.
Lösning: \( \quad \quad\; 10 \; \cdot \; 0,333\,333\,\ldots \; = \; 3,333\,333\,\ldots \qquad\qquad {\rm (I)} \)
Lösning: \( \quad\;\;\, \underline{\quad\; 1 \;\, \cdot \; 0,333\,333\,\ldots \; = \; 0,333\,333\,\ldots} \qquad\qquad {\rm (II)} \)
- \[{\rm (I)-(II)} \quad\quad\! 9 \;\; \cdot \; 0,333\,333\,\ldots \; = \; 3 \]
- \[ \quad\, 0,333\,333\,\ldots \: = \: \displaystyle{3 \over 9} \; = \; {1 \cdot \cancel{\color{Red} 3} \over 3 \cdot \cancel{\color{Red} 3}} \]
- \[ \quad\, 0,333\,333\,\ldots \: = \: \displaystyle{1 \over 3} \]
b) Skriv \( \; \displaystyle{1 \over 3} \; \) till decimaltal.
Lösning:
Låt miniräknaren dividera \( \, 1 \,/\, 3 \, \) så får du:
- \[ \quad\, \displaystyle{1 \over 3} \: = \: 0,333\,333\,\ldots \]
Samma resultat skulle även manuell division \( \, 1 \,/\, 3 \, \) ge, vilket vi dock inte vill genomföra här.
Icke-periodisk decimalutveckling
Så kallas decimaltal som har oändligt många decimaler utan något upprepande mönster (utan period), t.ex.:
- \[\sqrt{2} \; = \; 1,4142135623730950488016887\ldots \, \]
Detta decimaltal är en icke-periodisk decimalutveckling, för det har inte bara oändligt många decimaler. Det har framför allt inga grupper av siffror som upprepas, dvs det har ingen period. Därför kan decimaltalet inte skrivas i bråkform.
Därmed är \( \sqrt{2} \, \) inget rationellt utan ett irrationellt tal, se även Olika typer av tal. Ändå är \( \, \sqrt{2} \cdot \sqrt{2} \; = \; 2 \, \) dvs ett heltal.
Ett annat exempel är talet \( \, \pi \). Det finns oändligt många irrationella tal. Inget sådant kan skrivas i bråkform.
Det enda sättet att praktiskt hantera dem är att avrunda dem. Hur man gör det och lite mer visas i underavsnittet Avrundning och värdesiffror.
Internetlänkar
https://www.elevspel.se/amnen/matematik/539-decimaltal.html
http://www.youtube.com/watch?v=6aGAzibVJ5M
http://nomp.se/nomp/#/!/matematik/52/braktal/ova-pa-skriv-braktal-som-decimaltal/52.FRACTIONS.3
https://www.youtube.com/watch?v=kTWP-n9-PEM
Copyright © 2011-2015 Math Online Sweden AB. All Rights Reserved.