Skillnad mellan versioner av "1.1 Fördjupning till Polynom"

Versionen från 15 maj 2015 kl. 16.08

Repetition: Ekvationer & Potenser

Genomgång

Övningar

Fördjupning

Nästa demoavsnitt -->

Lektion 1 Polynom

Lektion 2 Polynom: Fördjupning

Digital beräkning av nollställen

Här ska vi lära oss att använda vår grafritande miniräknare för att bestämma ett polynoms nollställe. Detta sker i flera steg:

Bestämma lämpliga min-/max-värden för att kunna se polynomfunktionens graf i räknarens displayfönster.

Rita grafen och avläsa närmevärden för nollställena från grafen.

Använda räknarens ekvationslösare för att utgående från ett närmevärde bestämma nollstället med den noggrannhet som krävs.

Exempel

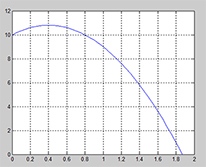
Marie tävlar i simhopp från 10-meterstorn. Hennes hopp följer en bana som beskrivs av funktionen:

\[ y = 10 + 4\,x - 5\,x^2 \]

där \( \, y \, \) är hennes höjd över vattnet i meter och \( \, x \, \) är tiden i sekunder efter hon lämnat brädan.

a) Vilken maximal höjd når Marie?

Använd din grafritande räknare för att genomföra följande uppgifter:

b) Undersök vilka min- och max-värden samt vilken skala man lämpligast bör använda på \( \, x\)- och \( \, y\)-axeln för att rita funktionens graf. Ange min-/max-värdena i din räknares WINDOW.

c) Rita funktionens graf i din räknare.

d) När slår Marie i vattnet? Använd din räknares ekvationslösare för att bestämma polynomets nollställe dvs lösa 2:a gradspolynomekvationen:

\[ - 5\,x^2 + 4\,x + 10 = 0 \]

Ange svaret med 4 decimaler.

Lösning

a) Maries bana följer en parabel eftersom den beskrivs av 2:a gradspolynomfunktionen:

\[ y = - 5\,x^2 + 4\,x + 10 \]

Eftersom den kvadratiska termen har negativ koefficient är grafen en parabel som är öppen nedåt och har därmed ett maximum. Parabler är alltid symmetriska kring symmetrilinjen som går genom maximipunkten. Så för hitta maximipunkten måste vi ställa upp symmetrilinjens ekvation. Det in sin tur kräver att vi skriver 2:a gradspolynomekvationen ovan i normalform, dvs så att koefficienten till den kvadratiska termen blir \( \, 1 \). Därför:

\[\begin{align} - 5\,x^2 + 4\,x + 10 & = 0 & | \;\; / (-5) \\ x^2 - 0,8\,x - 2 & = 0 \end{align}\]

Detta är normalformen med \( p = -0,8\, \). Formeln för symmetrilinjens ekvation är:

\[ x = -{p \over 2} \]

Därmed blir symmetrilinjens ekvation:

\[ x = -{-0,8 \over 2} = 0,4 \]

Maximipunkten har alltså koordinaterna:

\[\begin{align} x & = 0,4 \\ y & = (- 5) \cdot 0,4\,^2 + 4 \cdot 0,4 + 10 = 10,8 \end{align}\]

Maries maximala höjd blir \( \underline{10,8\,\,{\rm m}}\).

b) Tittar man på Maries bana kan man se att höjden \( \, y \, \) är \( \, 10 \, \) när tiden \( \, x \, \) är \( \, 0 \):

\[ y = - 5\,x^2 + 4\,x + 10 \]

Eftersom både höjden och tiden är positiva kommer banan stanna i koordinatsystemets första kvadrant. Därför är det lämpligt att välja för både \( \, x\)- och \( \, y\)-axelns min-värdet \( \, 0 \):

\[ x_{min}\, = 0 \]

\[ y_{min}\, = 0 \]

Eftersom Marie enligt a) når en maximalhöjd på \( \, 10,8 \) m kan man välja ett lite större max-värde på \( \, y\)-axeln, säg \( \, 12 \, \). Om x-axeln vet vi bara att symmetrilinjen går genom x = 0,4. Om hon efter 0,4 sek når sin maximala höjd gissar vi att hon slår i vattnet kanske innan 2 sek. Därför:

\[ x_{max}\, = 2 \]

\[ y_{max}\, = 12 \]

Pga de lite annorlunda storleksordningar på x- och \( \, y\)-axeln är det kanske lämpligt att välja skalan \( \, 1 \, \) på \( \, x\)- och \( \, 10 \, \) på \( \, y\)-axeln:

\[ x_{scl}\, = 1 \]

\[ y_{scl}\, = 10 \]

Alla dessa värden är inte exakta och kan variera lite beroende på räknarens typ. Samma sak är det med instruktioner som följer.

Hur som helst, tryck på knappen WINDOW i räknaren och ange där inställningarna ovan. Låt resten stå.

c) Nu är vi redo att rita grafen.

Tryck på knappen Y= och skriv in funktionsuttrycket där markören står.

Efter inmatningen ska stå där:

Y1=(-)5X^2+4X+10

Tryck på ENTER.

Tryck på knappen GRAPH.

Grafen till höger borde ritas om allt har gått bra:

Din räknares display har kanske ett lite annorlunda utseende. Men kurvan borde vara den samma.

Framför allt borde kurvans skärningspunkt med \( \, x\)-axeln visa det samma ungefärliga värdet, nämligen \( \, 1,9 \, \). Dvs polynomets nollställe är \(\,\approx 1,9 \) eller höjden y är 0 (Marie slår i vattnet) efter \( \, x\, \approx 1,9 \, \) sek.

Vi kan använda detta närmevärde i nästa steg som startvärde för kalkylatorns ekvationslösare som kommer att precisera polynomets nollställe.

d) Tryck i miniräknaren på knappen MATH.

Gå med piltangentern till Solver...

Tryck på ENTER.

Mata in polynomet där markören står så att det efteråt står följande två rader i displayen:

EQUATION SOLVER

eqn:0=(-)5X^2+4X+10

Tryck först på knappen ALPHA (orange) och sedan på SOLVE (i orange ovanpå ENTER).

Mata in startvärdet \( x\, \approx 1,9 \) som vi fick fram i c) och tryck en gång till på först ALPHA och sedan SOLVE.

Värdet x = 1,8696938456... visas i displayen vilket betyder:

Marie slår i vattnet efter \( \underline{1,8697\,\,{\rm sek}}\).

Polynomfunktioner av högre grad

När ett polynom tilldelas en annan variabel, säg \( \, y \, \) bildas en polynomfunktion. I Matte 1-kursen hade vi bara linjära eller 1:a gradsfunktioner av typ:

\[ y = 4\,x + 12 \]

Till höger om likhetstecknet står ett polynom där \( \, x \, \) förekommer som 1:a gradspotens dvs med exponenten \( \, 1 \, \). Därför kallas \( \, 4\,x \, \) polynomets linjära term. Polynomets konstanta term är \( \, 12 \). Grafen till denna 1:a gradsfunktion är en rät linje. I Matte 2-kursen gick vi ett steg vidare och sysslade med 2:a gradsfunktioner av typ:

\[ y = 3\,x^2 + 5\,x - 16 \]

Här är graden \( \, 2 \). Den kvadratiska termen är \( \, 3\,x^2 \, \), den linjära termen \( \, 5\,x\, \) och den konstanta termen \( \, -16 \). Grafen till denna 2:a gradfunktion är en parabel. Dessa funktioner kallas polynomfunktioner därför att uttrycken till höger om likhetstecken är polynom, dvs summor av termer där exponenterna till \( \, x\)-potenserna är positiva heltal eller \( \, 0 \). I Matte 3-kursen ska vi nu lära oss att hantera även polynom av högre grad än \( \, 2 \).

Exempel på polynomfunktion av högre grad

Vi tar som exempel följande 4:e gradspolynomfunktion:

\[ y = x^4 - 29\;x^2 + 100 \]

vars graf till höger är mer komplicerad än en parabel.

Den har framför allt fler minima, maxima och nollställen.

Funktionens fyra nollställen är identiska med lösningarna till 4:e gradsekvationen:

\[ x^4 - 29\;x^2 + 100 = 0 \]

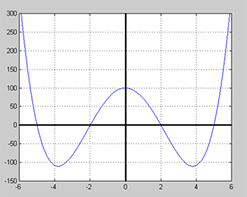
Ett polynoms grad är ett mått på dess komplexitet. För att se hur komplexiteten växer med graden ska vi titta på följande sex polynom vars grafer är ritade i samma koordinatsystem. Man ser att kurvorna svänger oftare och får fler maxima/minima ju högre deras grad är:

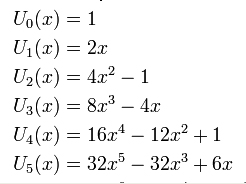Fil:Chebyshev Polyn 2nd 60.jpg

Polynomen \(U_n(x)\,\) bildar en familj eller följd av polynom där varje polynom har ett index \( \, n \,\) som samtidigt är polynomets grad.

De nedsänkta indexen \(_0,\,_1,\,_2,\,_3,\,_4,\,_5\) i beteckningarna \(U_0, U_1, U_2, U_3, U_4, U_5\,\) används här både för att relatera indexet till polynomets grad och kunna sedan (några rader längre fram) skriva en formel för dessa polynom som kommer att visa hur de hänger ihop som en familj.

Dessa polynom kallas efter den ryske matematikern Chebyshev som presenterade dem 1854. De är relaterade till varandra med följande rekursionsformel:

\( U_n(x) = 2\,x\,\cdot\,U_{n-1}(x)\,-\,U_{n-2}(x) \qquad\qquad n = 2, 3, ... \)

\( U_0(x) = 1, \quad U_1(x) = 2\,x \)

Denna formel ger oss möjligheten att ta fram Chebyshevpolynomen rekursivt (successivt). Detta betyder att vi kan ställa upp ett polynom med hjälp av de två föregående. De första två Chebyshevpolynomen \( \, U_0, \, U_1 \, \) är explicit angivna (i den andra raden). Det tredje Chebyshevpolynomet \(U_2\,\) får man genom att sätta in \( \, U_0, \, U_1 \,\) i högerledet av rekursionsformeln (i den första raden). Det fjärde Chebyshevpolynomet \( \, U_3 \, \) får man genom att sätta in \( \, U_1, \, U_2 \, \) i högerledet osv.

Alla Chebyshevpolynom definieras och genereras av rekursionsformeln ovan därför att de kan beräknas utgående från de två första. Ett exempel visas nedan. Förfarandet är rekursivt eftersom man ställer upp nästa polynom med hjälp av de två föregående.

Exempel på räkning med polynom

Ställ upp de Chebyshevpolynomen \( \, U_2, \, U_3, \, U_4\,\) med hjälp av de två första \( \, U_0, \, U_1 \).

\[ \displaystyle U_0(x) = \underline{1} \]

\[ U_1(x) = \underline{2\,x} \]

För \(n = 2\,\) ger rekursionsformeln:

\[ U_2(x) = 2\,x\,\cdot\,U_1(x)\,-\,U_0(x) = 2\,x\,\cdot\,2\,x\,-\,1 = \underline{4\,x^2\,-\,1} \]

Sedan kan vi få fram \( U_3(x) \) genom att att sätta in n = 3 i rekursionsformeln:

\[ U_3(x) = 2\,x\,\cdot\;U_2(x)\,-\,U_1(x) = 2\,x\,\cdot\,(4\,x^2\,-\,1)\,-\,2\,x = 8\,x^3\,-\,2\,x\,-\,2\,x = \underline{8\,x^3\,-\,4\,x} \]

För \(n = 4\,\) ger rekursionsformeln \( U_4(x) \) osv.:

\[ U_4(x) = 2\,x\,\cdot\,U_3(x)\,-\,U_2(x) = 2\,x\,\cdot\,(8\,x^3\,-\,4\,x)\,-\,(4\,x^2\,-\,1) = 16\,x^4\,-\,8\,x^2\,-\,4\,x^2\,+\,1 = \underline{16\,x^4\,-\,12\,x^2\,+\,1} \]

Jämförelse av koefficienter

Jämförelse av koefficienter är en teknik eller en metod som vi kommer att använda för att lösa högre gradsekvationer genom att faktorisera polynom av högre grad än 2, se övningarna 10-12. Metoden bygger på begreppet likhet mellan polynom.

Definition: \( \quad \) Två polynom

\[ \; P(x) = a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad \ldots \quad + a_1 \cdot x + a_0 \]

\[ \; Q(x) = b_n \cdot x^n + b_{n-1} \cdot x^{n-1} + \quad \ldots \quad + b_1 \cdot x + b_0 \]

är lika med varandra om de har samma grad och om alla deras motsvarande koefficienter, dvs om:

\[ \; a_n = b_n, \qquad a_{n-1} = b_{n-1}, \qquad \ldots \qquad a_1 = b_1, \qquad a_0 = b_0 \]

Exempel 1

Följande två polynom är givna där \( a\, \) och \( b\, \) är konstanter medan \( x\, \) är polynomens oberoende variabel:

\[ P(x) = a \cdot x + 2\,a + b \]

\[ Q(x) = 2\,x + 1\!\, \]

För vilka värden på \( a\, \) och \( b\, \) är de två polynomen lika med varandra?

Lösning:

Vi skriver \( P(x),\, \) och \( Q(x)\, \) så att vi lättare kan se motsvarande koefficienter:

\[ P(x) = a \cdot x^1 + (2\,a + b) \cdot x^0 \]

\[ Q(x) = 2 \cdot x^1 + \quad\;\; 1 \quad\;\; \cdot x^0 \]

Jämförelse av koefficienterna till \( x^1\, \) leder till:

\[ a = 2\,\]

Jämförelse av koefficienterna till \( x^0 \,\) leder till:

\[ 2\,a + b = 1\!\,\]

Sätter man in \( a = 2\, \) i denna relation får man \( b = -3\, \).

Polynomen \( P(x)\, \) och \( Q(x)\, \) är lika med varandra för:

\[ a = 2\, \]

\[ b = -3\, \]

Exempel 2

Följande 3:e gradspolynom är givet

\[ P(x) = x^3 + 4\,x^2 + x - 26 \]

Hitta ett 2:a gradspolynom \( Q(x)\, \) så att:

\[ Q(x)\cdot (x-2) = P(x) \]

Lösning:

Det 2:a gradspolynomet \( Q(x)\, \) kan skrivas så här:

\[ Q(x) = a\,x^2 + b\,x + c \]

Vi bestämmer koefficienterna \( a\, , \, b\, \) och \( c\, \) så att \( {\color{White} x} Q(x)\cdot (x-2) \, = \, P(x) \)

\[\begin{array}{rclc} Q(x) \cdot (x - 2) & = & (a\,x^2 + b\,x + c)\cdot (x - 2) & = \\ & = & a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c & = \\ & = & a\,x^3 + (-2\,a + b)\,x^2 + (-2\,b + c)\,x - 2\,c & = \\ & = & a \cdot x^3 + (-2\,a + b) \cdot x^2 + (-2\,b + c) \cdot x - 2\,c \cdot x^0 & \\ P(x) & = & 1 \cdot x^3 + \quad\;\;\;\;4 \quad\;\; \cdot x^2 + \quad\;\;\;\,1 \quad\;\; \cdot x - 26 \cdot x^0 \end{array} \]

Jämförelse av koefficienterna till \( x^3 \)-termen ger:

\[ a = 1 \]

Jämförelse av koefficienterna till \( x^2 \)-termen ger:

\[\begin{align} -2\,a + b & = 4 \\ -2\cdot 1 + b & = 4 \\ - 2 + b & = 4 \\ b & = 6 \\ \end{align} \]

Jämförelse av koefficienterna till \( x^1 \)-termen ger:

\[\begin{align} -2\,b + c & = 1 \\ -2\cdot 6 + c & = 1 \\ -12 + c & = 1 \\ c & = 13 \\ \end{align} \]

Jämförelse av koefficienterna till \( x^0 \, \)-termen bekräftar värdet på \( c \, \):

\[\begin{align} - 2\,c & = - 26 \\ c & = 13 \\ \end{align} \]

Vi får \( a = 1\, , \, b = 6\, \) och \( c = 13\, \) och därmed:

\[ Q(x) = x^2 + 6 \, x + 13 \]

Anmärkningar

I litteraturen förekommer även ett annat namn för den metod som beskrevs ovan. Istället för jämförelse av koefficienter som vi använder pratar man om metoden med obestämda koefficienter (eng.: the method of undetermined coefficients). Med obestämda koefficienter menar man den ansats som man i början gör med obestämda koefficienter som man sedan bestämmer under metodens gång.

I några kursböcker behandlas polynomdivision istället för jämförelse av koefficienter, för att åstadkomma faktorisering av högre gradspolynom. Vi menar att det algebraiskt är besvärligare med polynomdivision. Jämförelse av koefficienter åstadkommer samma sak med mindre arbete och ger dessutom mer insikt i polynomens struktur.

@@ Rad 34: / Rad 34: @@
 :::<math> y = 10 + 4\,x - 5\,x^2 </math>
-där y är hennes höjd över vattnet i meter och x är tiden i sekunder efter hon lämnat brädan.
+där <math> \, y \, </math> är hennes höjd över vattnet i meter och <math> \, x \, </math> är tiden i sekunder efter hon lämnat brädan.
 <b>a)</b> &nbsp; Vilken maximal höjd når Marie?
@@ Rad 40: / Rad 40: @@
 Använd din grafritande räknare för att genomföra följande uppgifter:
-<b>b)</b> &nbsp; Undersök vilka min- och max-värden samt vilken skala man lämpligast bör använda på x- och y-axeln för att rita funktionens graf. Ange min-/max-värdena i din räknares WINDOW.
+<b>b)</b> &nbsp; Undersök vilka min- och max-värden samt vilken skala man lämpligast bör använda på <math> \, x</math>- och <math> \, y</math>-axeln för att rita funktionens graf. Ange min-/max-värdena i din räknares WINDOW.
 <b>c)</b> &nbsp; Rita funktionens graf i din räknare.
@@ Rad 60: / Rad 60: @@
 :::<math> y = - 5\,x^2 + 4\,x + 10 </math>
-Eftersom den kvadratiska termen har negativ koefficient är grafen en parabel som är öppen nedåt och har därmed ett maximum. Parabler är alltid symmetriska kring symmetrilinjen som går genom maximipunkten. Så för hitta maximipunkten måste vi ställa upp symmetrilinjens ekvation. Det in sin tur kräver att vi skriver 2:a gradspolynomekvationen ovan i normalform, dvs så att koefficienten till den kvadratiska termen blir 1. Därför:
+Eftersom den kvadratiska termen har negativ koefficient är grafen en parabel som är öppen nedåt och har därmed ett maximum. Parabler är alltid symmetriska kring symmetrilinjen som går genom maximipunkten. Så för hitta maximipunkten måste vi ställa upp symmetrilinjens ekvation. Det in sin tur kräver att vi skriver 2:a gradspolynomekvationen ovan i normalform, dvs så att koefficienten till den kvadratiska termen blir <math> \, 1 </math>. Därför:
 :::<math>\begin{align} - 5\,x^2 + 4\,x + 10 & = 0   & | \;\; / (-5) \\
@@ Rad 94: / Rad 94: @@
 :::<math> y_{min}\, = 0 </math>
-Eftersom Marie enligt <b>a)</b> når en maximalhöjd på <math> \, 10,8 </math> m kan man välja ett lite större max-värde på y-axeln, säg <math> \, 12 \, </math>. Om x-axeln vet vi bara att symmetrilinjen går genom x = 0,4. Om hon efter 0,4 sek når sin maximala höjd gissar vi att hon slår i vattnet kanske innan 2 sek. Därför:
+Eftersom Marie enligt <b>a)</b> når en maximalhöjd på <math> \, 10,8 </math> m kan man välja ett lite större max-värde på <math> \, y</math>-axeln, säg <math> \, 12 \, </math>. Om x-axeln vet vi bara att symmetrilinjen går genom x = 0,4. Om hon efter 0,4 sek når sin maximala höjd gissar vi att hon slår i vattnet kanske innan 2 sek. Därför:
 :::<math> x_{max}\, = 2 </math>
@@ Rad 100: / Rad 100: @@
 :::<math> y_{max}\, = 12 </math>
-Pga de lite annorlunda storleksordningar på x- och y-axeln är det kanske lämpligt att välja skalan <math> \, 1 \, </math> på <math> \, x</math>- och <math> \, 10 \, </math> på <math> \, y</math>-axeln:
+Pga de lite annorlunda storleksordningar på x- och <math> \, y</math>-axeln är det kanske lämpligt att välja skalan <math> \, 1 \, </math> på <math> \, x</math>- och <math> \, 10 \, </math> på <math> \, y</math>-axeln:
 :::<math> x_{scl}\, = 1 </math>