Skillnad mellan versioner av "1.1 Lösning 5a"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 1: | Rad 1: | ||
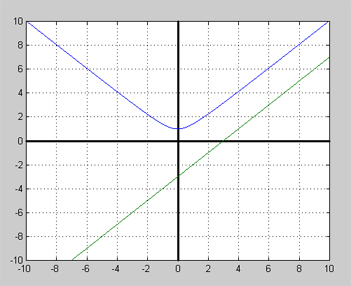
| − | Lösningen av övning 4b visar graferna till <math> y_1 = \sqrt{x^2 + 1} </math> (blå kurva) och <math> | + | Lösningen av övning 4b visar att ekvationen <math> \sqrt{x^2 + 1} = x - 3 </math> saknar lösning. Därför skär graferna till <math> y_1 = \sqrt{x^2 + 1} </math> (blå kurva) och <math> y_2 = x - 3\, </math> (grön linje) inte varandra: |
[[Image: Rotekv_Övn_4bR.jpg]] | [[Image: Rotekv_Övn_4bR.jpg]] | ||
| − | Den räta linjens lutning är 1. Grafen visar att man behöver bara höja denna lutning för att få en skärningspunkt mellan kurvan och linjen. En höjning av lutningen till t.ex. 3 skulle räcka för en skärningspunkt. Därför borde följande rotekvation | + | Den räta linjens lutning är 1. Grafen visar att man endast behöver bara höja denna lutning för att få en skärningspunkt mellan kurvan och linjen. En höjning av lutningen till t.ex. 3 skulle räcka för en skärningspunkt. Därför borde följande rotekvation ha en sann rot: |
<math> \sqrt{x^2 + 1} = 3\,x - 3 </math> | <math> \sqrt{x^2 + 1} = 3\,x - 3 </math> | ||
Versionen från 30 januari 2011 kl. 21.50
Lösningen av övning 4b visar att ekvationen \( \sqrt{x^2 + 1} = x - 3 \) saknar lösning. Därför skär graferna till \( y_1 = \sqrt{x^2 + 1} \) (blå kurva) och \( y_2 = x - 3\, \) (grön linje) inte varandra:
Den räta linjens lutning är 1. Grafen visar att man endast behöver bara höja denna lutning för att få en skärningspunkt mellan kurvan och linjen. En höjning av lutningen till t.ex. 3 skulle räcka för en skärningspunkt. Därför borde följande rotekvation ha en sann rot\[ \sqrt{x^2 + 1} = 3\,x - 3 \]