Skillnad mellan versioner av "3.5 Lösning 8a"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 1: | Rad 1: | ||
| − | |||
| − | |||
<table> | <table> | ||
<tr> | <tr> | ||
| Rad 7: | Rad 5: | ||
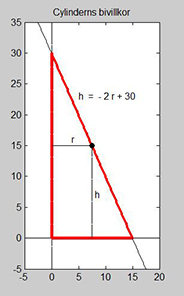
uppgiftens figur i den. Vi väljer cylinders radie <math> \, r \, </math> som horisontell | uppgiftens figur i den. Vi väljer cylinders radie <math> \, r \, </math> som horisontell | ||
| − | och dess höjd <math> \, h \, </math> som vertikal axel. | + | och dess höjd <math> \, h \, </math> som vertikal axel. Kons mantellinje |
| − | + | (från basytans kant till konens spets) blir då en rät linje. Cylinderns | |
| − | + | övre högra hörn (svarta punkten i figuren) rör sig på denna räta linje | |
| − | ::<math> {\color{Red} | + | vars ekvation är: |
| + | |||
| + | ::<math> {\color{Red} h} \, = \, k\,r \, + \, m </math> | ||
Lutningen <math> \, k \, = \, \displaystyle {\Delta y \over \Delta x} \, = \, - \, {20 \over 30} \, = \, - \, {2 \over 3} </math> | Lutningen <math> \, k \, = \, \displaystyle {\Delta y \over \Delta x} \, = \, - \, {20 \over 30} \, = \, - \, {2 \over 3} </math> | ||
Versionen från 3 februari 2015 kl. 20.32
| Vi inför ett koordinatsystem och sätter den röda triangeln från
uppgiftens figur i den. Vi väljer cylinders radie \( \, r \, \) som horisontell och dess höjd \( \, h \, \) som vertikal axel. Kons mantellinje (från basytans kant till konens spets) blir då en rät linje. Cylinderns övre högra hörn (svarta punkten i figuren) rör sig på denna räta linje vars ekvation är:
Lutningen \( \, k \, = \, \displaystyle {\Delta y \over \Delta x} \, = \, - \, {20 \over 30} \, = \, - \, {2 \over 3} \) Skärningspunkten med \(\,y\)-axeln: \( \quad m \, = \, 20 \) Den räta linjens ekvation blir då:
|
 |
Detta samband mellan \( \, x \, \) och \( \, {\color{Red} y} \,\) är problemets bivillkor.
