Skillnad mellan versioner av "3.5 Extremvärdesproblem"
Taifun (Diskussion | bidrag) m (→Exempel 1 Glasskiva) |
Taifun (Diskussion | bidrag) m (→Exempel 1 Glasskiva) |
||
| Rad 31: | Rad 31: | ||
'''Lösning:''' | '''Lösning:''' | ||
| − | a) | + | a) Vi inför beteckningen <math> \; {\color{Red} y} \; </math> för glasplattans andra sida, så att rektangelns area kan skrivas som: |
| − | + | ||
| − | Vi inför beteckningen <math> \; {\color{Red} y} \; </math> för glasplattans andra sida, så att rektangelns area kan skrivas som: | + | |
::::<math> A\,(x, {\color{Red} y}) \; = \; x \; \cdot \; {\color{Red} y} </math> | ::::<math> A\,(x, {\color{Red} y}) \; = \; x \; \cdot \; {\color{Red} y} </math> | ||
| Rad 51: | Rad 49: | ||
Den räta linjens ekvation i <math>\,k</math>-form: | Den räta linjens ekvation i <math>\,k</math>-form: | ||
| − | ::<math> y \, = \, k\,x \, + \, m </math> | + | ::<math> {\color{Red} y} \, = \, k\,x \, + \, m </math> |
Lutningen <math> \, k \, = \, \displaystyle {\Delta y \over \Delta x} \, = \, - \, {20 \over 30} \, = \, - \, {2 \over 3} </math> | Lutningen <math> \, k \, = \, \displaystyle {\Delta y \over \Delta x} \, = \, - \, {20 \over 30} \, = \, - \, {2 \over 3} </math> | ||
| Rad 57: | Rad 55: | ||
Skärningspunkten med <math>\,y</math>-axeln<span style="color:black">:</span> <math> \quad m \, = \, 20 </math> | Skärningspunkten med <math>\,y</math>-axeln<span style="color:black">:</span> <math> \quad m \, = \, 20 </math> | ||
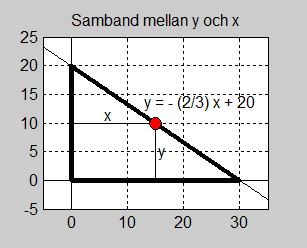
| − | Den räta linjens ekvation blir då<span style="color:black">:</span> <math> \quad \displaystyle y \, = \, - \, {2 \over 3}\,x \, + \, 20 </math> | + | Den räta linjens ekvation blir då<span style="color:black">:</span> <math> \quad \displaystyle {\color{Red} y} \, = \, - \, {2 \over 3}\,x \, + \, 20 </math> |
Denna ekvation kan uppfattas som det samband mellan <math> \, {\color{Red} y} \,</math> och <math> \, x \, </math>. | Denna ekvation kan uppfattas som det samband mellan <math> \, {\color{Red} y} \,</math> och <math> \, x \, </math>. | ||
| Rad 67: | Rad 65: | ||
Vi sätter in sambandet ovan i <math> \; A\,(x, {\color{Red} y}) = x \cdot {\color{Red} y} \; </math> för att eliminera <math> \, {\color{Red} y} \,</math> och ställa upp ett uttryck för arean som endast beror av <math> \, x </math>: | Vi sätter in sambandet ovan i <math> \; A\,(x, {\color{Red} y}) = x \cdot {\color{Red} y} \; </math> för att eliminera <math> \, {\color{Red} y} \,</math> och ställa upp ett uttryck för arean som endast beror av <math> \, x </math>: | ||
| − | ::<math> A(x) \, = \, x \cdot y \, = \, x \cdot (-\,{2 \over 3}\,x \, + \, 20) \, = \, -\,{2 \over 3}\,x^2 \, + \, 20\,x </math> | + | ::<math> A\,(x, {\color{Red} y}) \, = \, x \cdot {\color{Red} y} \, = \, x \cdot (-\,{2 \over 3}\,x \, + \, 20) \, = \, -\,{2 \over 3}\,x^2 \, + \, 20\,x </math> |
Versionen från 25 januari 2015 kl. 14.54
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
Lektion 33 Extremvärdesproblem I
Lektion 34 Extremvärdesproblem II
Innehåll
Exempel 1 Glasskiva
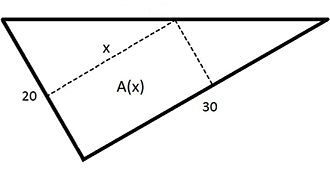
En glasskiva har formen av en rätvinklig triangel med följande mått i cm:
Ur skivan ska en rektangulär glasplatta skäras ut så att glasplattans area \( \, A(x) \, \) blir maximal.
a) Ställ upp arean \( \, A(x) \, \) som en funktion som endast beror av \( \, x \, \).
b) Bestäm \( \, x \, \) så att funktionen \( \, A(x) \, \) antar sitt maximum.
c) Beräkna glasplattans maximala area.
Lösning:
a) Vi inför beteckningen \( \; {\color{Red} y} \; \) för glasplattans andra sida, så att rektangelns area kan skrivas som:
- \[ A\,(x, {\color{Red} y}) \; = \; x \; \cdot \; {\color{Red} y} \]
Men här är \( \, A\,(x, {\color{Red} y}) \, \) en funktion av två variabler som vi inte kan jobba med. För att skriva om den till en funktion av endast en variabel, nämligen \( \, x \, \), måste vi hitta ett samband mellan \( \, x \, \) och \( \, {\color{Red} y} \, \). Dvs \( \, {\color{Red} y} \, \) måste uttryckas med \( \, x \, \) och på så sätt elimineras.
Detta samband bestäms rektangelns "fria" hörn som är bunden till triangelns hypotenusa. Det hörnet måste ju alltid ligga på hypotenusan.
Vi sätter in sambandet ovan i \( \; A\,(x, {\color{Red} y}) = x \cdot {\color{Red} y} \; \) för att eliminera \( \, {\color{Red} y} \,\) och ställa upp ett uttryck för arean som endast beror av \( \, x \):
- \[ A\,(x, {\color{Red} y}) \, = \, x \cdot {\color{Red} y} \, = \, x \cdot (-\,{2 \over 3}\,x \, + \, 20) \, = \, -\,{2 \over 3}\,x^2 \, + \, 20\,x \]