Skillnad mellan versioner av "3.3 Lösning 5b"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 2: | Rad 2: | ||
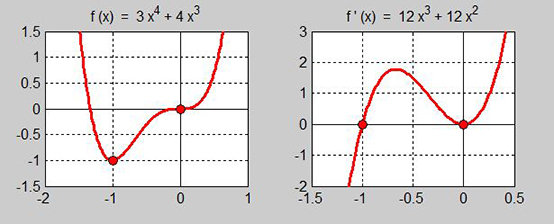
| − | Funktionens graf till vänster visar att <math> f(x) \;\; {\rm har\;i} \;\; (0, 0) \;\; {\rm | + | Funktionens graf till vänster visar att <math> f(x) \;\; {\rm har\;en\;terasspunkt\;i} \;\; (0, 0) \;\; {\rm och\;en\;minimipunkt\;i} \;\; (-1, -1) </math>. |
Derivatans graf till höger visar att <math> f'(x) \;\; {\rm har\;nollställen\;i} \;\; x = 0 \;\; {\rm och\;i} \;\; x = -1 </math>. | Derivatans graf till höger visar att <math> f'(x) \;\; {\rm har\;nollställen\;i} \;\; x = 0 \;\; {\rm och\;i} \;\; x = -1 </math>. | ||
Versionen från 10 januari 2015 kl. 13.21
Funktionens graf till vänster visar att \( f(x) \;\; {\rm har\;en\;terasspunkt\;i} \;\; (0, 0) \;\; {\rm och\;en\;minimipunkt\;i} \;\; (-1, -1) \).
Derivatans graf till höger visar att \( f'(x) \;\; {\rm har\;nollställen\;i} \;\; x = 0 \;\; {\rm och\;i} \;\; x = -1 \).
Derivatans nollställe i \( \, x = 0 \, \) är en dubbelrot vilket tyder på att funktionen har en terasspunkt där.
Derivatans nollställe i \( \, x = -1 \, \) är av enkel typ vilket tyder på att funktionen har en minimipunkt där.