Skillnad mellan versioner av "3.2 Lösning 10a"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 5: | Rad 5: | ||
På så sätt blir hypotenusan del av en rät linje med negativ lutning. Vi kallar rektangelns andra sida för <math> \, y \,</math>. Punkten <math> \, (x, y) \, </math> rör sig på denna rät linje. | På så sätt blir hypotenusan del av en rät linje med negativ lutning. Vi kallar rektangelns andra sida för <math> \, y \,</math>. Punkten <math> \, (x, y) \, </math> rör sig på denna rät linje. | ||
| − | Den räta linjens ekvation i <math>\,k</math>-form | + | Den räta linjens ekvation i <math>\,k</math>-form: |
::<math> y \, = \, k\,x \, + \, m </math> | ::<math> y \, = \, k\,x \, + \, m </math> | ||
| Rad 17: | Rad 17: | ||
::<math> m \, = \, 20 </math> | ::<math> m \, = \, 20 </math> | ||
| − | + | Den räta linjens ekvation blir då: | |
::<math> y \, = \, - \, {2 \over 3}\,x \, + \, 20 </math> | ::<math> y \, = \, - \, {2 \over 3}\,x \, + \, 20 </math> | ||
| − | + | Denna ekvation kan uppfattas som sambandet mellan <math> \, y \,</math> och <math> \, x \, </math> som bestäms av att rektangelns "fria" hörn är bunden till rektangelns hypotenusa. | |
| − | + | Vi använder sambandet ovan för att ställa upp ett uttryck för arean <math> \, A(x) \, </math> som endast beror av <math> \, x \, </math>. | |
::<math> A(x) \, = \, x \cdot y \, = \, x \cdot (- \, {2 \over 3}\,x \, + \, 20) \, = \, </math> | ::<math> A(x) \, = \, x \cdot y \, = \, x \cdot (- \, {2 \over 3}\,x \, + \, 20) \, = \, </math> | ||
Versionen från 26 december 2014 kl. 12.03
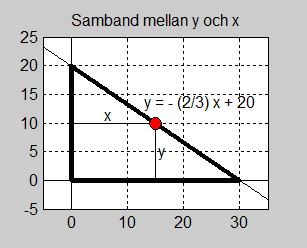
Vi inför ett koordinatsystem så att triangelns längre katet faller på \( x\)- och den kortare på \( y\)-axeln och den räta vinkeln hamnar i origo:
På så sätt blir hypotenusan del av en rät linje med negativ lutning. Vi kallar rektangelns andra sida för \( \, y \,\). Punkten \( \, (x, y) \, \) rör sig på denna rät linje.
Den räta linjens ekvation i \(\,k\)-form:
- \[ y \, = \, k\,x \, + \, m \]
Lutningen \(\,k\):
- \[ k \, = \, - \, {20 \over 30} \, = \, - \, {2 \over 3} \]
Skärningspunkten med \(\,y\)-axeln:
- \[ m \, = \, 20 \]
Den räta linjens ekvation blir då:
- \[ y \, = \, - \, {2 \over 3}\,x \, + \, 20 \]
Denna ekvation kan uppfattas som sambandet mellan \( \, y \,\) och \( \, x \, \) som bestäms av att rektangelns "fria" hörn är bunden till rektangelns hypotenusa.
Vi använder sambandet ovan för att ställa upp ett uttryck för arean \( \, A(x) \, \) som endast beror av \( \, x \, \).
- \[ A(x) \, = \, x \cdot y \, = \, x \cdot (- \, {2 \over 3}\,x \, + \, 20) \, = \, \]