Skillnad mellan versioner av "3.1 Lösning 8d"
Från Mathonline
Taifun (Diskussion | bidrag) (Skapade sidan med 'Från a)-c) vet vi: För alla <math> {\color{White} x} x < 3 {\color{White} x} </math> är <math>\, f(x) </math> avtagande. För alla <math> {\color{White} x} x > 3 {\...') |
Taifun (Diskussion | bidrag) m |
||
| Rad 1: | Rad 1: | ||
Från a)-c) vet vi: | Från a)-c) vet vi: | ||
| − | För alla <math> {\color{White} | + | För alla <math> {\color{White} {xxxxxx}} x < 1 \; </math> är <math>\, f(x) </math> växande. |
| − | För alla | + | I intervallet <math> \; 1 < x < 5 \; </math> är <math> \, f(x) </math> avtagande. |
| + | |||
| + | För alla <math> {\color{White} {xxxxxx}} x > 5 \; </math> är <math>\, f(x) </math> växande. | ||
<math> f(x) \, </math> har ett minimum i derivatans nollställe <math> \, x = 3 \, </math>. | <math> f(x) \, </math> har ett minimum i derivatans nollställe <math> \, x = 3 \, </math>. | ||
Versionen från 5 december 2014 kl. 11.02
Från a)-c) vet vi:
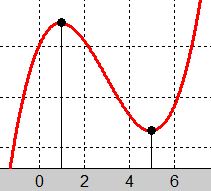
För alla \( {\color{White} {xxxxxx}} x < 1 \; \) är \(\, f(x) \) växande.
I intervallet \( \; 1 < x < 5 \; \) är \( \, f(x) \) avtagande.
För alla \( {\color{White} {xxxxxx}} x > 5 \; \) är \(\, f(x) \) växande.
\( f(x) \, \) har ett minimum i derivatans nollställe \( \, x = 3 \, \).
\( \, f(x) \, \) kan vara en tredjegradsfunktion.
Dessa informationer ger följande skiss: