Skillnad mellan versioner av "1.5a Lösning 10c"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 1: | Rad 1: | ||
[[Image: Övn 10.png]] | [[Image: Övn 10.png]] | ||
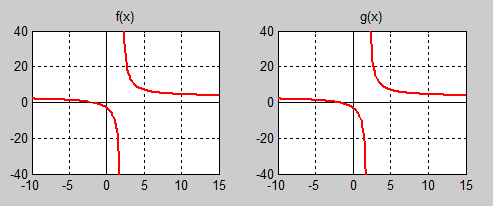
| − | Till synes visar resultatet helt identiska kurvor. Men | + | Till synes visar resultatet helt identiska kurvor. Men från övningens a)-del vet vi: |
| + | |||
| + | Funktionen <math> f(x)\, </math> har två diskontinuiteter: | ||
| + | |||
| + | <math> x_1 = -2 {\color{White} x} </math> är en hävbar diskontinuitet. | ||
| + | |||
| + | <math> x_2 = 2 \, {\color{White} xx} </math> är en icke-hävbar diskontinuitet. | ||
| + | |||
| + | Den hävbara diskontinuiteten <math> x_1 = -2\, </math> ses | ||
| + | |||
| + | |||
| + | |||
| + | är funktionen <math> f(x)\, </math> inte är definierad för <math> x = -3\, </math> och har en diskontinuitet där. Därför har dess graf (kurvan till vänster) ett "hål" eller en "lucka" i <math> x = -3\, </math> som man inte ser med blotta ögat. Så grafen lurar oss. Vi måste hålla oss till <math> f(x)\, </math>:s funktionsuttryck ovan som klart visar <u>två</u> diskontinuiteter, en i <math> x = -3\, </math> och den andra i <math> x = 3\, </math>. Den första som vi lyckades få bort genom förkortning, är en s.k. <strong><span style="color:red">hävbar diskontinuitet</span></strong> medan den andra är icke-hävbar. | ||
Versionen från 17 juli 2014 kl. 12.02
Till synes visar resultatet helt identiska kurvor. Men från övningens a)-del vet vi:
Funktionen \( f(x)\, \) har två diskontinuiteter\[ x_1 = -2 {\color{White} x} \] är en hävbar diskontinuitet.
\( x_2 = 2 \, {\color{White} xx} \) är en icke-hävbar diskontinuitet.
Den hävbara diskontinuiteten \( x_1 = -2\, \) ses
är funktionen \( f(x)\, \) inte är definierad för \( x = -3\, \) och har en diskontinuitet där. Därför har dess graf (kurvan till vänster) ett "hål" eller en "lucka" i \( x = -3\, \) som man inte ser med blotta ögat. Så grafen lurar oss. Vi måste hålla oss till \( f(x)\, \):s funktionsuttryck ovan som klart visar två diskontinuiteter, en i \( x = -3\, \) och den andra i \( x = 3\, \). Den första som vi lyckades få bort genom förkortning, är en s.k. hävbar diskontinuitet medan den andra är icke-hävbar.