Skillnad mellan versioner av "1.5 Övningar till Kontinuerliga och diskreta funktioner"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m (→Övning 4) |
||
| Rad 68: | Rad 68: | ||
::<math> y = x^2\, </math> | ::<math> y = x^2\, </math> | ||
| − | vars definitionsmängd är alla heltal mellan -5 och 5 dvs <math> -5 \leq x \ | + | vars definitionsmängd är alla heltal mellan -5 och 5 dvs <math> -5 \leq x \leq 5 </math>. |
Undersök om din grafräknare kan rita diskreta funktioner, annars rita manuellt på rutat papper. | Undersök om din grafräknare kan rita diskreta funktioner, annars rita manuellt på rutat papper. | ||
</div>{{#NAVCONTENT:Svar 4|1.5a Svar 4|Lösning 4|1.5a Lösning 4}} | </div>{{#NAVCONTENT:Svar 4|1.5a Svar 4|Lösning 4|1.5a Lösning 4}} | ||
Versionen från 11 juli 2014 kl. 10.52
| <-- Förra avsnitt | Teori | Övningar | Fördjupning | Nästa avsnitt --> |
E-övningar: 1-6
Övning 1
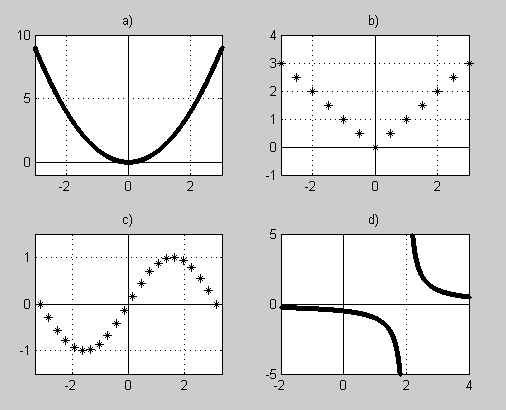
Bestäm för varje graf om den visar en diskret eller en kontinuerlig funktion.
Ange även om och i så fall för vilka \( x \, \) funktionerna har diskontinuiteter.
Motivera dina svar.
Övning 2
Anta att varje ruta i grafen nedan har längdenheten \( 1\, \).
a) Är funktionen \( f(x)\, \) diskret eller kontinuerlig?
b) Vilket värde kan du läsa av från grafen för funktionen \( f(x)\, \) för \( x = 4\, \)?
c) För vilka \( x\, \) är funktionen \( f(x)\, \) inte definierad i det ritade intervallet?
d) För vilka \( x\, \) är funktionen \( f(x)\, \) inte kontinuerlig i det ritade intervallet?
Motivera dina svar.
Övning 3
Anta att varje ruta i grafen nedan har längdenheten \( 1\, \).
a) Vilket värde kan du läsa av från grafen för funktionen \( f(x)\, \) för \( x = 4\, \)?
b) Är funktionen \( f(x)\, \) definierad för alla \( x\, \) i det ritade intervallet?
c) Är funktionen \( f(x)\, \) kontinuerlig för alla \( x\, \) i det ritade intervallet?
d) För vilka \( x\, \) är funktionen \( f(x)\, \) kontinuerlig och för vilka är den diskontinuerlig?.
Motivera dina svar.
Övning 4
Rita grafen till den diskreta funktionen:
- \[ y = x^2\, \]
vars definitionsmängd är alla heltal mellan -5 och 5 dvs \( -5 \leq x \leq 5 \).
Undersök om din grafräknare kan rita diskreta funktioner, annars rita manuellt på rutat papper.
 Hämtar...
Hämtar...