Skillnad mellan versioner av "2.3 Gränsvärde"

Från Mathonline
Hoppa till: navigering, sök
m
m
Rad 11: Rad 11:
  
  
−
[[File: Lektion_14_Gransvarde_Ruta.pdf|<b><span style="color:blue">Lektion 14 Gränsvärde</span></b>]]
+
[[Media: Lektion_14_Gransvarde_Rutac.pdf|<b><span style="color:blue">Lektion 14 Gränsvärde</span></b>]]
 +
 
  
 
<big>
 
<big>
−
Förutsättning i detta avsnitt är att alla funktioner <math> \; y \, = \, f(x) \; </math> är [[1.5_Kontinuerliga_och_diskreta_funktioner|<b><span style="color:blue">kontinuerliga</span></b>]] i alla punkter av det betraktade området.
+
Vårt mål i detta kapitel är att förstå begreppet <b><span style="color:red">derivata</span></b>. Men eftersom derivata är ett gränsvärde, måste vi först behandla begreppet gränsvärde.
 +
 
 +
 
 +
<big><b><span style="color:#931136">Introduktion till gränsvärde</span></b></big> <!-- &nbsp; <b>Uppgift 3438 (3c-boken, sid 190):</b> -->
 +
<table>
 +
<tr>
 +
<td><div class="ovnE0">
 +
<small>En fallskärmshoppare faller fritt med hastigheten
 +
 
 +
<math> \qquad\quad\;\;\; </math> <div class="smallBoxVariant"><math> v(t) = 80\,(1 - 0,88\,^t) </math></div>
 +
 
 +
där <math> \, t = \, </math> tiden i sek. Finns det en maximal hastighet
 +
 
 +
<math> \, v_{max} \, </math> som hopparen inte kan överskrida?
 +
 
 +
Om ja, bestäm den.</small>
 +
</div>
 +
</td>
 +
  <td><math> \quad </math></td>
 +
  <td>[[Image: 5_186_Uppg_3438_Fritt_fall_250.jpg]]
 +
</td>
 +
</tr>
 +
</table>
 +
<b>Grafisk och fysikalisk tolkning:</b>
 +
 
 +
Grafen till <math> \, v(t) \, </math> visar att det finns en maximal hastighet som hopparen inte kan överskrida:
 +
 
 +
Efter ca. 40 sek blir hopparens hastighet konstant<span style="color:black">:</span> <math> \;\; v \, \approx \, v_{max} = 80 </math> m/s. <math> \;\; </math> [https://www.naturvetenskap.org/fysik/gymnasiefysik/kraft/newtons-1a-lag/ <b><span style="color:blue">Newtons fösta lag</span></b>]:
 +
 
 +
När ett föremål är i vila eller rör sig med konstant hastighet är summan av alla krafter <math> \, = 0 \, </math> (och omvänt).
 +
 
 +
Därav följer<span style="color:black">:</span> <math> \qquad </math> Luftmotstånd <math> \, \approx \, </math> gravitation <math> \qquad </math> dvs <math> \qquad </math> rörelsen är ett fritt fall med luftmotstånd.
 +
 
 +
<b>Matematisk beskrivning:</b>
 +
 
 +
<div class="border-divblue"><b><span style="color:red">Gränsvärdet</span></b>&nbsp; för <math> \, 80\,(1 - 0,88\,^t) \, </math>,&nbsp; då <math> \,t \, </math> går mot <math> \, \infty \; </math>,&nbsp; <b><span style="color:red">är <math> \, 80</math></span></b>.<br>Man skriver<span style="color:black">:</span> <math> \quad </math> <div class="smallBoxVariant"><math> \displaystyle {\color{Red} {\lim_{t \to \infty}}}\,{\left(80\,(1 - 0,88\,^t)\right)} \color{Red} { \; = \; 80} </math></div> <math> \quad </math> och läser<span style="color:black">:</span>
 +
 
 +
<math> \qquad\;\; </math> Limes av <math> \, 80\,(1 - 0,88\,^t) \, </math>, då <math> t </math> går mot <math> \infty \, </math>, är <math> 80 </math>.
 +
 
 +
<math> \quad\;\;\, {\color{Red} {\lim}} \, </math> står för det latinska ordet <math> \, {\color{Red} {\rm limes}} \, </math> som betyder gräns.
 +
</div>
 +
 
 +
<b>Limes kan beräknas:</b>
 +
 
 +
<math> v_{max} \, = \, \displaystyle \lim_{t \to \infty}\,{(80\,(1 - 0,88\,^t))} \, = \, \lim_{t \to \infty}\,{(80 - 80\cdot0,88\,^t)} \, = \, \lim_{t \to \infty}\,{80} - \lim_{t \to \infty}\,{(80\cdot0,88\,^t)} \, = \, 80 \, - \, 0 \, = \, \color{Red} {80} \, </math>,
 +
 
 +
eftersom <math> \qquad\;\; \displaystyle \lim_{t \to \infty}\,{(80\cdot0,88\,^t)} \, = \, \lim_{t \to \infty}\,{80} \cdot \lim_{t \to \infty}\,{(0,88\,^t)} \, = \, 80 \cdot 0 \, = \, 0 \quad </math> pga <math> \quad 0,88 \, < \, 1 \; </math>.
  
−
Vårt mål är att definiera begreppet <b><span style="color:red">derivata</span></b>. Men eftersom derivata är ett gränsvärde, måste vi förstå vad ett gränsvärde är för något, närmare bestämt:
 
  
 
=== <b><span style="color:#931136">Gränsvärde för en funktion</span></b> ===
 
=== <b><span style="color:#931136">Gränsvärde för en funktion</span></b> ===
 +
Vi förutsätter att alla funktioner <math> \, y = f(x) \, </math> i detta avsnitt är [[1.5_Kontinuerliga_och_diskreta_funktioner|<b><span style="color:blue">kontinuerliga</span></b>]] för alla <math> \, x \, </math> i det betraktade området.
  
 
<div class="exempel">
 
<div class="exempel">
Rad 33: Rad 80:
 
<math> \quad\qquad\qquad\qquad\, \displaystyle {\color{Red} {\lim_{x \to \infty}}}\,{10 \over x\,-\,2} {\color{Red} { \; = \; 0}} </math>
 
<math> \quad\qquad\qquad\qquad\, \displaystyle {\color{Red} {\lim_{x \to \infty}}}\,{10 \over x\,-\,2} {\color{Red} { \; = \; 0}} </math>
 
</div>
 
</div>
−
:Läs så här<span style="color:black">:</span> <math> \qquad {\rm Limes\;\,av} \; \displaystyle{10 \over x\,-\,2} \; , \;\; {\rm då} \; x \; {\rm går\;mot} \, \infty \; , \;\; {\rm är} \;\, 0 {\rm .}</math>
 
  
−
:Symbolen&nbsp;&nbsp;<math> {\color{Red} {\lim}} </math>&nbsp;&nbsp;står för det latinska ordet&nbsp;&nbsp;<math> {\color{Red} {\rm limes}} </math>&nbsp; som betyder gräns.
+
 
 +
'''Grafiskt''':&nbsp; Kurvan närmar sig <math> \, x </math>-axeln när <math> \, x \, </math> växer, dvs <math> \, y\, </math> blir allt mindre ju större <math> \, x \, </math> blir.
 +
 
 +
Men kurvan skär aldrig <math> \, x </math>-axeln. Funktionen går mot <math> \, 0\, </math> utan att nå <math> \, 0 </math>.  
 
</td>
 
</td>
 
</tr>
 
</tr>
 
</table>
 
</table>
−
'''Grafiskt''':&nbsp; Kurvan närmar sig <math> \, x </math>-axeln när <math> \, x \, </math> växer, dvs <math> \, y\, </math> blir allt mindre ju större <math> \, x \, </math> blir. Men kurvan skär aldrig <math> \, x </math>-axeln. Funktionen går mot <math> \, 0\, </math> utan att nå <math> \, 0 </math>.
+
'''Analytiskt''':&nbsp; Ekvationen <math> \, \displaystyle {10 \over x\,-\,2} \, = \, 0 \, </math> saknar lösning, därför att täljaren <math> \, 10\, </math> är en konstant som aldrig kan bli <math> \, 0 </math>. Så kan inte heller hela uttrycket i vänsterled bli <math> \, 0 \, </math> oavsett <math> \, x </math>. Nämnaren växer däremot obegränsat när <math> \, x \, </math> växer. Därför går hela uttrycket i vänsterled mot <math> \, 0 </math>.
−
 
+
−
'''Algebraiskt''':&nbsp; Ekvationen <math> \, \displaystyle {10 \over x\,-\,2} \, = \, 0 \, </math> saknar lösning, därför att täljaren <math> \, 10\, </math> är en konstant som aldrig kan bli <math> \, 0 </math>. Så kan inte heller hela uttrycket i vänsterled bli <math> \, 0 \, </math> oavsett <math> \, x </math>. Nämnaren växer däremot obegränsat när <math> \, x \, </math> växer. Därför går hela uttrycket i vänsterled mot <math> \, 0 </math>.
+
  
 
Man säger<span style="color:black">:</span> <math> \; \displaystyle {10 \over x\,-\,2} \; {\rm går\;mot} \, 0 \; {\rm när} \; x \; {\rm går\;mot} \, \infty \, </math>, kort<span style="color:black">:</span> <math> \;\; \displaystyle {10 \over x\,-\,2} \to 0 \quad {\rm när} \quad x \to \infty \;\; </math>, bättre uttryckt<span style="color:black">:</span> <math> \, \boxed{ \displaystyle \lim_{x \to \infty}\,{10 \over x\,-\,2} \, = \, 0} \, </math>.
 
Man säger<span style="color:black">:</span> <math> \; \displaystyle {10 \over x\,-\,2} \; {\rm går\;mot} \, 0 \; {\rm när} \; x \; {\rm går\;mot} \, \infty \, </math>, kort<span style="color:black">:</span> <math> \;\; \displaystyle {10 \over x\,-\,2} \to 0 \quad {\rm när} \quad x \to \infty \;\; </math>, bättre uttryckt<span style="color:black">:</span> <math> \, \boxed{ \displaystyle \lim_{x \to \infty}\,{10 \over x\,-\,2} \, = \, 0} \, </math>.
Rad 51: Rad 98:
  
  
−
"Paradoxen" att funktionen allt mer närmar sig <math> \, 0 \, </math> utan att någonsin bli <math> \, 0 </math>, löses upp och kan därmed hanteras algebraiskt med hjälp av <b><span style="color:red">limes</span></b> som generellt beskriver fenomenet att närma sig ett värde allt mer utan att nå det någonsin.  
+
"Paradoxen" att funktionen allt mer närmar sig <math> \, 0 \, </math> utan att någonsin bli <math> \, 0 </math>, löses upp och kan därmed hanteras analytiskt med hjälp av <b><span style="color:red">limes</span></b> som generellt beskriver fenomenet att närma sig ett värde allt mer utan att nå det någonsin.  
  
−
Limesbegreppet är centralt inom <b><span style="color:red">Analys</span></b><math>-</math> den gren av matematiken som [https://sv.wikipedia.org/wiki/Isaac_Newton <b><span style="color:blue">Newton</span></b>] och [https://sv.wikipedia.org/wiki/Gottfried_Wilhelm_von_Leibniz <b><span style="color:blue">Leibniz</span></b>] på 1700-talet la grunden till, även kallad <b><span style="color:red">Differential- och Integralkalkyl</span></b>, på engelska <b><span style="color:red">Calculus</span></b>.  
+
Limesbegreppet är centralt inom <b><span style="color:red">Analys</span></b><math>-</math> den gren av matematiken som [https://sv.wikipedia.org/wiki/Isaac_Newton <b><span style="color:blue">Newton</span></b>] och [https://sv.wikipedia.org/wiki/Gottfried_Wilhelm_von_Leibniz <b><span style="color:blue">Leibniz</span></b>] på 1700-talet la grunden till, även kallad <b><span style="color:red">Differential- och Integralkalkyl</span></b>, på engelska <b><span style="color:red">Calculus</span></b>. Det är därför vi numera använder begreppet "analytiskt" istället för "algebraiskt".
  
−
I detta kapitel kommer vi att använda limes för att definiera derivatan algebraiskt som ett gränsvärde. För att kunna göra det måste vi lära oss att <b><span style="color:red">beräkna</span></b> gränsvärden.
+
I detta kapitel kommer vi att använda limes för att definiera derivatan analytiskt som ett gränsvärde. För att kunna göra det måste vi lära oss att <b><span style="color:red">beräkna</span></b> gränsvärden.
 
</big>
 
</big>
  
Rad 142: Rad 189:
 
::<math> x^2 - x - 6 = 0 \, </math>
 
::<math> x^2 - x - 6 = 0 \, </math>
  
−
<math>p</math>-<math> q</math>-formeln kan användas, men enligt [[Detta avsnitt ingår inte i demon.|<b><span style="color:blue">Vieta</span></b>]] gäller för lösningarna <math> \, x_1\,</math> och <math> \, x_2 \, </math> (går snabbare) <span style="color:black">:</span>
+
<math>p</math>-<math> q</math>-formeln kan användas, men enligt [[1.2_Repetition_Faktorisering_%26_Vieta_från_Matte_2#Vietas_formler_-_samband_mellan_koefficienter_och_nollst.C3.A4llen|<b><span style="color:blue">Vieta</span></b>]] gäller för lösningarna <math> \, x_1\,</math> och <math> \, x_2 \, </math> (går snabbare) <span style="color:black">:</span>
  
 
::<math> \begin{align} x_1  +  x_2 & = -(-1) = 1  \\
 
::<math> \begin{align} x_1  +  x_2 & = -(-1) = 1  \\
Rad 226: Rad 273:
 
Jämför även med förra avsnittets [[2.2_Genomsnittlig_förändringshastighet#Exempel_2_Kvadratisk_funktion|<b><span style="color:blue">Exempel 2 Kvadratisk funktion</span></b>]]<span style="color:black">:</span>
 
Jämför även med förra avsnittets [[2.2_Genomsnittlig_förändringshastighet#Exempel_2_Kvadratisk_funktion|<b><span style="color:blue">Exempel 2 Kvadratisk funktion</span></b>]]<span style="color:black">:</span>
  
−
<math> y \, = \, \boxed{2\,x} \, </math> är derivatan av <math> \, y \, = \, x^2 \, </math>, se [[Detta avsnitt ingår inte i demon.|<b><span style="color:blue">derivatan som en ny funktion</span></b>]].
+
<math> y \, = \, \boxed{2\,x} \, </math> är derivatan av <math> \, y \, = \, x^2 \, </math>, se [[2.4_Derivatans_definition#Derivatan_som_en_ny_funktion|<b><span style="color:blue">derivatan som en ny funktion</span></b>]].
 
</div>
 
</div>
−
 
−
 
−
<big>
 
−
=== <b><span style="color:#931136">Existens av gränsvärden</span></b> ===
 
−
 
−
Inledningsvis bestämdes i detta avsnitt [[2.3_Gränsvärde#Exempel|<b><span style="color:blue">gränsvärdet</span></b>]] av <math> \, \displaystyle \lim_{x \to \infty}\,{10 \over x\,-\,2} \, </math> till <math> \, 0 \, </math> utan att fråga om den överhuvudtaget ''existerade''. Själva bestämmandet av gränsvärdet <math> \, 0 \, </math> bevisade ju existensen. Men det finns faktiskt fall där ett gränsvärde ''inte'' existerar och därför inte heller kan bestämmas.
 
−
 
−
Som exempel tar vi samma funktion som i det inledande [[2.3_Gränsvärde#Exempel|<b><span style="color:blue">exemplet</span></b>]], men byter frågeställningen: 
 
−
 
−
<div class="exempel">
 
−
==== <b><span style="color:#931136">Exempel på att gränsvärde saknas</span></b> ====
 
−
 
−
Funktionen <math> y = f(x) = \displaystyle {10 \over x\,-\,2} </math> är given<span style="color:black">:</span> <math> \qquad\qquad\qquad </math> <b><span style="color:red">Vad händer med <math> \, y \, </math> när <math> \; x \to 2 \; </math>?</span></b>
 
−
<table>
 
−
<tr>
 
−
  <td>Dvs bestäm <math> \qquad\quad \displaystyle \lim_{\color{Red} {x \to 2}}\,{10 \over x\,-\,2} </math>
 
−
 
−
'''Svar:''' <math> \quad\;\; f(x)\, </math> är inte definierad för <math> x = 2\, </math>.
 
−
 
−
<math> \qquad\qquad\qquad\qquad\quad \Downarrow </math>
 
−
 
−
<div class="border-divblue"><math> \displaystyle \lim_{\color{Red} {x \to 2}}\,{10 \over x\,-\,2} \quad </math> <b>existerar inte</b>&nbsp;&nbsp;&nbsp;<span style="color:black">:</span>
 
−
 
−
 
−
<math> \qquad </math> <b><span style="color:red">Gränsvärde saknas.</span></b>
 
−
</div>
 
−
</td>
 
−
  <td><math> \qquad </math></td>
 
−
  <td>[[Image: Ex 2 Gransvarde.jpg]]</td>
 
−
</tr>
 
−
</table>
 
−
 
−
Grafen visar att kurvan skjuter upp i höjden å ena sidan och ner i "djupet" å andra sidan av punkten <math> \, x = 2 </math>.
 
−
 
−
Algebraiskt är <math> \, f(x)\, </math> inte definierad för <math> x = 2\, </math>, för <math> \displaystyle{10 \over x\,-\,2} </math>:s nämnare blir <math> \, 0\, </math> för <math> \, x = 2 </math>.
 
−
 
−
Dessutom finns det två olika resultat beroende på om <math> \, x </math> går mot <math> \, 2 </math> från höger eller från vänster<span style="color:black">:</span>
 
−
 
−
<math> f(x)\, </math> går mot <math> +\, \infty </math> när man närmar sig <math> \, x = 2 </math> från höger och mot <math> -\, \infty </math> när man närmar sig <math> \, x = 2 </math> från vänster. Med pilar<span style="color:black">:</span>
 
−
 
−
<math> y \;\; {\rm går\;mot} \, +\infty \; {\rm när} \; x \; {\rm går\;mot} \, 2 \;{\rm från\;höger:} \; \qquad\quad y \to +\infty \quad {\rm när} \quad x \to 2^+ </math>
 
−
 
−
<math> y \;\; {\rm går\;mot} \, -\infty \; {\rm när} \; x \; {\rm går\;mot} \, 2 \;{\rm från\;vänster:} \; \qquad\; y \to -\infty \quad {\rm när} \quad x \to 2^- </math>
 
−
 
−
där <math> x \to 2^+ </math> betyder att närma sig <math> \, x = 2 </math> från höger (<math> \, x > 2 </math>) och <math> x \to 2^- </math> att närma sig <math> \, x = 2 </math> från vänster (<math> \, x < 2 </math>).
 
−
</div>
 
−
 
−
 
−
Följande modifierad variant av [[2.3_Gränsvärde#Exempel_2|<b><span style="color:blue">Exempel 2</span></b>]] (<math> \, {\color{Red} {x \to 0}} \, </math> istället för <math> \, x \to \infty </math>) visar samma sak:
 
−
</big>
 
−
 
−
 
−
<div class="ovnE">
 
−
 
−
==== <b><span style="color:#931136">Exempel 2 a</span></b> ====
 
−
 
−
Bestäm <math> \qquad \displaystyle \lim_{x \to 0}\, {4\,x\,+\,5 \over x} </math>
 
−
 
−
<b>Lösning:</b>
 
−
 
−
::<math> \lim_{x \to 0^+}\, {4\,x\,+\,5 \over x} \, = \, \lim_{x \to 0^+}\, \left(4 \,+\, {5 \over x}\right) \,= \, +\infty </math>
 
−
 
−
::<math> \lim_{x \to 0^-}\, {4\,x\,+\,5 \over x} \, = \, \lim_{x \to 0^-}\, \left(4 \,+\, {5 \over x}\right) \,= \, -\infty </math>
 
−
 
−
där <math> x \to 0^+ </math> betyder att närma sig <math> \, x = 0 </math> från höger (<math> \, x > 0 </math>) och <math> x \to 0^- </math> att närma sig <math> \, x = 0 </math> från vänster (<math> \, x < 0 </math>).
 
−
 
−
<b>Anmärkning:</b> Sättet att skriva limes som ovan förklaras nedan i [[2.3_Gr%C3%A4nsv%C3%A4rde#Ensidiga_och_oegentliga_gr.C3.A4nsv.C3.A4rden|<b><span style="color:blue">Ensidiga och oegentliga gränsvärden</span></b>]].
 
−
 
−
<b>Svar:</b> <math> \qquad\;\; </math> Gränsvärde saknas.
 
−
</div>
 
−
 
−
 
−
<big>
 
−
Men även om en funktion skulle gå mot t.ex. mot <math> +\,\infty </math>, för ett visst <math> \, x </math> både från höger och vänster, t.ex. <math> \displaystyle {f(x) = {1 \over x^2}} </math> för <math> \, x = 0 </math>, skulle det strikt matematiskt inte vara korrekt att säga att limes existerar och är <math> +\,\infty </math>, därför att <math> \infty </math> inte är något värde. Med andra ord: 
 
−
 
−
 
−
<div class="border-divblue">Ett gränsvärde måste, för att existera, vara både entydigt och ändligt.</div>
 
−
 
−
 
−
Därför är det matematiskt korrekt att säga: Gränsvärdena <math> \; \displaystyle {\lim_{x \to 2}\,{10 \over x - 2}} \; </math> och <math> \; \displaystyle {\lim_{x \to 0}\,{1 \over x^2}} \;</math> existerar inte.
 
−
</big>
 
−
 
−
 
−
<div class="ovnA">
 
−
=== <b><span style="color:#931136">Ensidiga och oegentliga gränsvärden</span></b> ===
 
−
 
−
Skiljer man närmandet från höger till <math> \, x = 2 \, </math> från närmandet från vänster kan man bilda s.k. <b><span style="color:red">ensidiga gränsvärden</span></b>:
 
−
 
−
:::<math> \lim_{x \to 2^{+}}\,{10 \over x - 2}\,=\,+\,\infty \qquad\quad \; {\rm och} \; \qquad\quad \lim_{x \to 2^{-}}\,{10 \over x - 2}\,=\,-\,\infty </math>
 
−
 
−
där <math> x \to 2^+ </math> betyder att närma sig <math> \, x = 2 </math> från höger (<math> \, x > 2 </math>) och <math> x \to 2^- </math> att närma sig <math> \, x = 2 </math> från vänster (<math> \, x < 2 </math>).
 
−
 
−
Man pratar om höger- och vänstergränsvärdet genom att skilja mellan de två sätten att närma sig talet <math> \, 2 </math> på <math> \, x</math>-axeln: från höger <math> x \to 2^+ </math> och från vänster <math> x \to 2^- </math>, därav beteckningen <b><span style="color:red">ensidig</span></b>. I vårt exempel ger de också två olika resultat.
 
−
 
−
Gränsvärden av funktioner som går mot oändligheten (och därmed strikt talat inte existerar), men ändå skrivs med limessymbolen, kallar man <b><span style="color:red">oegentliga gränsvärden</span></b>.
 
−
 
−
<div class="exempel">
 
−
==== <b><span style="color:#931136">Exempel</span></b> ====
 
−
<table>
 
−
<tr>
 
−
  <td>
 
−
 
−
<math> \qquad\qquad\qquad\qquad\qquad \displaystyle {\lim_{x \to 0}\,{1 \over x^2}}\,=\,+\,\infty </math>
 
−
 
−
 
−
Grafen visar att funktionen <math> \displaystyle f(x) = {1 \over x^2} </math> går mot <math> +\,\infty </math> både
 
−
 
−
när <math> \, x \to 0 </math> från höger (<math> \, x > 0 </math>) och från vänster (<math> \, x < 0 </math>). Visserligen
 
−
 
−
är gränsvärdet entydigt, men det är oändligt och kallas därför <b><span style="color:red">oegentligt</span></b>. 
 
−
 
−
 
−
Däremot är <math> \displaystyle \lim_{x \to 2}\,{10 \over x - 2} </math> varken entydigt eller ändligt. Därför existerar det inte.
 
−
</td>
 
−
  <td><math> \qquad </math></td>
 
−
  <td>[[Image: y = 1 genom x^2.jpg]]</td>
 
−
</tr>
 
−
</table>
 
−
 
−
Att man använder det ovannämnda skrivsättet för ensidiga och oegentliga gränsvärden sker av praktiska skäl. Man ersätter pilarna som vi använde inledningsvis med att beskriva gränsprocessen med limessymbolen istället. Det är bekvämt att använda en enhetlig notation för att beskriva gränsprocesser. Är man medveten om att limes enligt den strikta definitionen inte existerar, är det o.k.
 
−
 
−
OBS! Av skrivsättet för ensidiga och oegentliga gränsvärden följer fortfarande <b><span style="color:red">inte</span></b> att <math> \; \displaystyle {\lim_{x \to 2}\,{10 \over x - 2}} \; </math> eller <math> \; \displaystyle {\lim_{x \to 0}\,{1 \over x^2}} \; </math> <b><span style="color:red">existerar</span></b>.
 
−
</div>
 
−
 
−
 
−
</div>
 
−
 
−
 
−
 
  
  
Rad 366: Rad 284:
  
 
https://www.youtube.com/watch?v=fPOX0QX8AH0
 
https://www.youtube.com/watch?v=fPOX0QX8AH0
−
</big>
 
  
  
Rad 374: Rad 291:
  
  
−
[[Matte:Copyrights|Copyright]] © 2011-2016 Taifun Alishenas. All Rights Reserved.
+
 
 +
 
 +
 
 +
[[Matte:Copyrights|Copyright]] © 2011-2017 Taifun Alishenas. All Rights Reserved.

Versionen från 21 oktober 2017 kl. 15.40

        <<  Förra avsnitt          Genomgång          Övningar          Fördjupning          Nästa demoavsnitt  >>      


Lektion 14 Gränsvärde


Vårt mål i detta kapitel är att förstå begreppet derivata. Men eftersom derivata är ett gränsvärde, måste vi först behandla begreppet gränsvärde.


Introduktion till gränsvärde

En fallskärmshoppare faller fritt med hastigheten

\( \qquad\quad\;\;\; \)
\( v(t) = 80\,(1 - 0,88\,^t) \)

där \( \, t = \, \) tiden i sek. Finns det en maximal hastighet

\( \, v_{max} \, \) som hopparen inte kan överskrida?

Om ja, bestäm den.

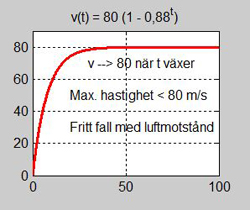
\( \quad \) 5 186 Uppg 3438 Fritt fall 250.jpg

Grafisk och fysikalisk tolkning:

Grafen till \( \, v(t) \, \) visar att det finns en maximal hastighet som hopparen inte kan överskrida:

Efter ca. 40 sek blir hopparens hastighet konstant: \( \;\; v \, \approx \, v_{max} = 80 \) m/s. \( \;\; \) Newtons fösta lag:

När ett föremål är i vila eller rör sig med konstant hastighet är summan av alla krafter \( \, = 0 \, \) (och omvänt).

Därav följer: \( \qquad \) Luftmotstånd \( \, \approx \, \) gravitation \( \qquad \) dvs \( \qquad \) rörelsen är ett fritt fall med luftmotstånd.

Matematisk beskrivning:

Gränsvärdet  för \( \, 80\,(1 - 0,88\,^t) \, \),  då \( \,t \, \) går mot \( \, \infty \; \),  är \( \, 80\).
Man skriver: \( \quad \)
\( \displaystyle {\color{Red} {\lim_{t \to \infty}}}\,{\left(80\,(1 - 0,88\,^t)\right)} \color{Red} { \; = \; 80} \)
\( \quad \) och läser:

\( \qquad\;\; \) Limes av \( \, 80\,(1 - 0,88\,^t) \, \), då \( t \) går mot \( \infty \, \), är \( 80 \).

\( \quad\;\;\, {\color{Red} {\lim}} \, \) står för det latinska ordet \( \, {\color{Red} {\rm limes}} \, \) som betyder gräns.

Limes kan beräknas:

\( v_{max} \, = \, \displaystyle \lim_{t \to \infty}\,{(80\,(1 - 0,88\,^t))} \, = \, \lim_{t \to \infty}\,{(80 - 80\cdot0,88\,^t)} \, = \, \lim_{t \to \infty}\,{80} - \lim_{t \to \infty}\,{(80\cdot0,88\,^t)} \, = \, 80 \, - \, 0 \, = \, \color{Red} {80} \, \),

eftersom \( \qquad\;\; \displaystyle \lim_{t \to \infty}\,{(80\cdot0,88\,^t)} \, = \, \lim_{t \to \infty}\,{80} \cdot \lim_{t \to \infty}\,{(0,88\,^t)} \, = \, 80 \cdot 0 \, = \, 0 \quad \) pga \( \quad 0,88 \, < \, 1 \; \).


Gränsvärde för en funktion

Vi förutsätter att alla funktioner \( \, y = f(x) \, \) i detta avsnitt är kontinuerliga för alla \( \, x \, \) i det betraktade området.

Exempel

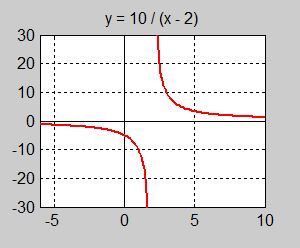
Funktionen \( y = f(x) = \displaystyle {10 \over x\,-\,2} \) är given: \( \qquad\qquad \) Vad händer med \( \, y \, \) när \( \; x \to \infty \; \)?

\( \quad \)Ex 1 Gransvarde.jpg \( \quad \)
Gränsvärdet  för \( \, \displaystyle {10 \over x\,-\,2} \, \),  då \( \,x \, \) går mot \( \, \infty \; \),  är \( \, 0\)  :


\( \quad\qquad\qquad\qquad\, \displaystyle {\color{Red} {\lim_{x \to \infty}}}\,{10 \over x\,-\,2} {\color{Red} { \; = \; 0}} \)


Grafiskt:  Kurvan närmar sig \( \, x \)-axeln när \( \, x \, \) växer, dvs \( \, y\, \) blir allt mindre ju större \( \, x \, \) blir.

Men kurvan skär aldrig \( \, x \)-axeln. Funktionen går mot \( \, 0\, \) utan att nå \( \, 0 \).

Analytiskt:  Ekvationen \( \, \displaystyle {10 \over x\,-\,2} \, = \, 0 \, \) saknar lösning, därför att täljaren \( \, 10\, \) är en konstant som aldrig kan bli \( \, 0 \). Så kan inte heller hela uttrycket i vänsterled bli \( \, 0 \, \) oavsett \( \, x \). Nämnaren växer däremot obegränsat när \( \, x \, \) växer. Därför går hela uttrycket i vänsterled mot \( \, 0 \).

Man säger: \( \; \displaystyle {10 \over x\,-\,2} \; {\rm går\;mot} \, 0 \; {\rm när} \; x \; {\rm går\;mot} \, \infty \, \), kort: \( \;\; \displaystyle {10 \over x\,-\,2} \to 0 \quad {\rm när} \quad x \to \infty \;\; \), bättre uttryckt: \( \, \boxed{ \displaystyle \lim_{x \to \infty}\,{10 \over x\,-\,2} \, = \, 0} \, \).

Vad händer med \( \, y \, \) när \( \; x \to - \infty \; \)?

Något liknande visas när \( \, x \, \) går mot negativa värden, dvs när \( x \to \, {\color{Red} {- \infty}} \):   \( \,y\, \) mot \( \,0\, \) bara att \( \, y\, \) nu närmar sig \( \, 0 \, \) nedifrån, kort: \( \;\; y \to 0 \quad {\rm när} \quad x \to {\color{Red} {- \infty}} \; \).


"Paradoxen" att funktionen allt mer närmar sig \( \, 0 \, \) utan att någonsin bli \( \, 0 \), löses upp och kan därmed hanteras analytiskt med hjälp av limes som generellt beskriver fenomenet att närma sig ett värde allt mer utan att nå det någonsin.

Limesbegreppet är centralt inom Analys\(-\) den gren av matematiken som Newton och Leibniz på 1700-talet la grunden till, även kallad Differential- och Integralkalkyl, på engelska Calculus. Det är därför vi numera använder begreppet "analytiskt" istället för "algebraiskt".

I detta kapitel kommer vi att använda limes för att definiera derivatan analytiskt som ett gränsvärde. För att kunna göra det måste vi lära oss att beräkna gränsvärden.


Beräkning av gränsvärden

I princip kan limes av en funktion beräknas genom att sätta in i funktionsuttrycket det värde som \( \,x \, \) ska gå emot. Men ofta ger detta odefinierade uttryck.

Därför måste man först förenkla uttrycket, ev. flera gånger. Sedan sätts in det värde som \( \,x \, \) ska gå emot, i funktionsuttrycket.


Exempel 1

Bestäm \( \qquad \displaystyle \lim_{x \to 0}\, {x^2 + 7\,x \over x} \)

Lösning:

För \( \, x = 0 \, \) är uttrycket \( \, \displaystyle{x^2 + 7\,x \over x} \, \) inte definierat därför att nämnaren blir \( \, 0 \).

Därför måste vi förenkla uttrycket.

Vi faktoriserar uttryckets täljare för att kolla om man ev. kan förkorta.

Täljaren kan faktoriseras genom att bryta ut \( x \, \):

\[ \lim_{x \to 0}\, {x^2 + 7\,x \over x} \, = \, \lim_{x \to 0}\, {{\color{Red} x}\:(x + 7) \over {\color{Red} x}} \, = \, \lim_{x \to 0}\, (x + 7) \, = \, 0 + 7 \, = \, 7 \]


Exempel 2

Bestäm \( \qquad \displaystyle \lim_{x \to \infty}\, {4\,x\,+\,5 \over x} \)

Lösning:

Vi förenklar uttrycket i limes genom att separera summan i uttrycket:

\[ {4\,x\,+\,5 \over x} = {4\,{\color{Red} x} \over {\color{Red} x}} \,+\,{5 \over x} \,=\, 4 \,+\, {5 \over x} \]

\( \displaystyle{5 \over x} \) går mot \( 0 \): \( \qquad \displaystyle \lim_{x \to \infty}\, {5 \over x} \, = \, 0 \)

Därför kan vi bestämma limes för hela uttrycket:

\[ \lim_{x \to \infty}\, {4\,x\,+\,5 \over x} \, = \, \lim_{x \to \infty}\, \left(4 \,+\, {5 \over x}\right) \,= \, 4\,+\,0 \,= \, 4 \;\, \]


Exempel 3

Bestäm \( \qquad \displaystyle \lim_{x \to 2}\, {x^2\,-\,4 \over 5\,x - 10} \)

Lösning:

Insättningen av \( \, x = 2 \, \) i uttrycket ger det odefinierade uttrycket \( \, \displaystyle{0 \over 0} \).

Vi faktoriserar både täljaren och nämnaren för att kolla om man ev. kan förkorta.

Täljaren kan faktoriseras med hjälp av konjugatreglen och nämnaren genom att bryta ut:

\[ x^2\,-\,4 = (x\,+\,2)\cdot(x\,-\,2) \]
\[ 5\,x - 10 = 5\,(x\,-\,2) \]

Nu kan vi förkorta uttrycket och beräkna limes:

\[ \lim_{x \to 2}\, {x^2\,-\,4 \over 5\,x - 10} \, = \, \lim_{x \to 2}\, {(x + 2) \cdot {\color{Red} {(x-2)}} \over 5\,{\color{Red} {(x-2)}}} \, = \, \lim_{x \to 2} \, {x + 2 \over 5} \, = \, {2 + 2 \over 5} \, = \, {4 \over 5} \, = \, 0,8 \]


Exempel 4

Bestäm \( \qquad \displaystyle \lim_{x \to 3}\, {x^2 - x - 6 \over x - 3} \)

Lösning:

Insättningen av \( \, x = 3 \, \) i uttrycket ger det odefinierade uttrycket \( \, \displaystyle{0 \over 0} \).

För att kunna se om man ev. kan förkorta uttrycket faktoriserar vi täljaren:

\[ x^2 - x - 6 = 0 \, \]

\(p\)-\( q\)-formeln kan användas, men enligt Vieta gäller för lösningarna \( \, x_1\,\) och \( \, x_2 \, \) (går snabbare) :

\[ \begin{align} x_1 + x_2 & = -(-1) = 1 \\ x_1 \cdot x_2 & = - 6 \end{align}\]

Två tal vars produkt är \( \, -6 \, \) är t.ex. \( \, 3 \, \) och \( \, -2 \). Men även deras summa är \( \, 1 \). Därför:

\[ \begin{align} x_1 & = 3 \\ x_2 & = - 2 \end{align}\]

Täljarens faktorisering blir då:

\[ x^2 - x - 6 = (x - 3) \cdot (x + 2) \]

Nu kan vi förkorta uttrycket mot nämnaren och beräkna limes:

\[ \lim_{x \to 3}\, {x^2 - x - 6 \over x - 3} \, = \, \lim_{x \to 3}\, {{\color{Red} {(x-3)}} \cdot (x + 2) \over {\color{Red} {(x-3)}}} \, = \, \lim_{x \to 3}\, (x + 2) \, = \, 3 + 2 \, = \, 5 \]


Exempel 5

Bestäm \( \qquad \displaystyle \lim_{x \to \infty}\,\, {x^3\,-\,2 \over 2\,x^3\,+\,3\,x\,-\,4} \)

Lösning:

För att förenkla uttrycket i limes divideras uttryckets täljare och nämnare med den högsta \( \,x\)-potensen, nämligen med \( \,x^3 \):

\[ \lim_{x \to \infty}\,\, {x^3\,-\,2 \over 2\,x^3\,+\,3\,x\,-\,4} \,=\, \lim_{x \to \infty}\,\, {x^3/x^3\,-\,2/x^3 \over 2\,x^3/x^3\,+\,3\,x/x^3\,-\,4/x^3} \,=\, \lim_{x \to \infty}\,\, {1\,-\,{\color{Red} {2/x^3}} \over 2\,+\,{\color{Blue} {3/x^2}}\,-\,{\color{ForestGreen} {4/x^3}}} \]


För att förenkla sista uttrycket använder vi:

\[ \lim_{x \to \infty}\, {\color{Red} {2 \over x^3}} \, = \, \lim_{x \to \infty}\, {\color{Blue} {3 \over x^2}} \, = \, \lim_{x \to \infty} \, {\color{ForestGreen} {4 \over x^3}} \, = \, 0 \]

Insatt i det sista uttrycket blir det:

\[ \lim_{x \to \infty}\,\, {x^3\,-\,2 \over 2\,x^3\,+\,3\,x\,-\,4} \,=\quad \cdots \quad = \, \lim_{x \to \infty}\,\, {1\,-\,{\color{Red} {2/x^3}} \over 2\,+\,{\color{Blue} {3/x^2}}\,-\,{\color{ForestGreen} {4/x^3}}} \,=\, {1\,-\,{\color{Red} 0} \over 2\,+\,{\color{Blue} 0}\,-\,{\color{ForestGreen} 0}} \,=\, {1 \over 2} \]


Exempel 6

Funktionen \( \; f(x) = x^2 \; \) är given.   Bestäm gränsvärdet \( \quad \displaystyle \lim_{h \to 0}\,\,{f(2+h) - f(2) \over h} \; \).

Lösning:

\[ f(2+h) \, = \, (2+h)\,^2 \, = \, {\color{Red} {4 + 4\,h + h\,^2}} \]
\[ f(2) \, = \, 2\,^2 \, = \, {\color{Blue} 4} \]
\[ \lim_{h \to 0}\,\,{f(2+h) - f(2) \over h} \, = \, \lim_{h \to 0} {{\color{Red} {4 + 4\,h + h\,^2}}\,\,-\,\,{\color{Blue} 4} \over h} = \lim_{h \to 0} {4\,h + h^2 \over h} = \]
\[ = \lim_{h \to 0} {{\color{Red} h}\,(4 + h) \over {\color{Red} h}} = \lim_{h \to 0} \, (4 + h) = 4 \]


Exempel 7

Funktionen \( \; f(x) = x^2 \; \) är given.   Bestäm gränsvärdet \( \quad \displaystyle \lim_{h \to 0}\,\,{f(x+h) - f(x) \over h} \; \).

Lösning:

Eftersom uttrycket i limes involverar två variabler \( \, x \, \) och \( \, h \, \) kommer limes inte längre vara ett tal utan ett uttryck i \( \, x \).

\( \displaystyle \lim_{\color{Red} {h \to 0}} \, \) innebär att gränsvärdet ska bildas för \( \, {\color{Red} {h \to 0}} \). Därför borde \( \, x\, \) under gränsprocessen anses som en konstant.

\[ {\color{Red} {f(x+h)}} \, = \, (x+h)^2 \, = \, {\color{Red} {x^2 + 2\,x\,h + h^2}} \]
\[ {\color{Blue} {f(x)}} \, = \, {\color{Blue} {x\,^2}} \]
\[ \lim_{h \to 0}\,\,{{\color{Red} {f(x+h)}} - {\color{Blue} {f(x)}} \over h} \, = \, \lim_{h \to 0} {{\color{Red} {x^2 + 2\,x\,h + h^2}} \, - \, {\color{Blue} {x\,^2}} \over h} \, = \, \lim_{h \to 0} {2\,x\,h + h^2 \over h} = \]
\[ = \lim_{h \to 0} {{\color{Red} h}\,(2\,x + h) \over {\color{Red} h}} = \lim_{h \to 0} \, (2\,x + h) = \boxed{2\,x} \]

Observera att Exempel 6 ovan är ett specialfall av detta exempel för \( x = 2 \, \).

Jämför även med förra avsnittets Exempel 2 Kvadratisk funktion:

\( y \, = \, \boxed{2\,x} \, \) är derivatan av \( \, y \, = \, x^2 \, \), se derivatan som en ny funktion.


Internetlänkar

https://www.youtube.com/watch?v=_oPD-c8IAzs

https://www.youtube.com/watch?v=StP64lMXZjA

https://www.youtube.com/watch?v=fPOX0QX8AH0






Copyright © 2011-2017 Taifun Alishenas. All Rights Reserved.

Hämtad från "https://minidemo.mathonline.se/index.php?title=2.3_Gränsvärde&oldid=27780"