Skillnad mellan versioner av "1.1 Lösning 5a"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 3: | Rad 3: | ||
[[Image: Rotekv_Övn_4bR.jpg]] | [[Image: Rotekv_Övn_4bR.jpg]] | ||
| − | Den räta linjens lutning är 1. Grafen visar att man endast behöver | + | Den räta linjens lutning är 1. Grafen visar att man endast behöver höja denna lutning för att få en skärningspunkt mellan kurvan och linjen. En höjning av lutningen till t.ex. 3 skulle räcka för en skärningspunkt. Därför borde följande rotekvation ha en sann rot: |
<math> \sqrt{x^2 + 1} = 3\,x - 3 </math> | <math> \sqrt{x^2 + 1} = 3\,x - 3 </math> | ||
Versionen från 30 januari 2011 kl. 21.51
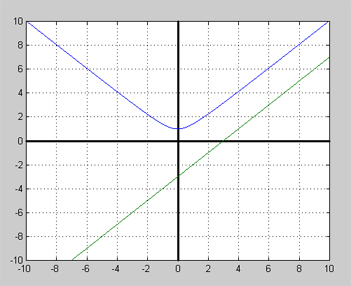
Lösningen av övning 4b visar att ekvationen \( \sqrt{x^2 + 1} = x - 3 \) saknar lösning. Därför skär graferna till \( y_1 = \sqrt{x^2 + 1} \) (blå kurva) och \( y_2 = x - 3\, \) (grön linje) inte varandra:
Den räta linjens lutning är 1. Grafen visar att man endast behöver höja denna lutning för att få en skärningspunkt mellan kurvan och linjen. En höjning av lutningen till t.ex. 3 skulle räcka för en skärningspunkt. Därför borde följande rotekvation ha en sann rot\[ \sqrt{x^2 + 1} = 3\,x - 3 \]