Skillnad mellan versioner av "3.5 Lösning 8a"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 19: | Rad 19: | ||
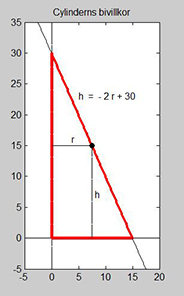
Skärningspunkten med <math>\,h</math>-axeln<span style="color:black">:</span> <math> \quad m \, = \, 30 </math>. | Skärningspunkten med <math>\,h</math>-axeln<span style="color:black">:</span> <math> \quad m \, = \, 30 </math>. | ||
| − | Den räta linjens ekvation och därmed problemets bivillkor blir | + | Den räta linjens ekvation och därmed problemets bivillkor blir<span style="color:black">:</span> |
::::::<math> h \, = \, - \, 2\,r \, + \, 30 </math> | ::::::<math> h \, = \, - \, 2\,r \, + \, 30 </math> | ||