Skillnad mellan versioner av "3.5 Lösning 6b"

Versionen från 2 februari 2015 kl. 11.58

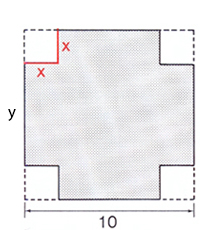
Från a) har vi problemets bivillkor:

\[ y \, = \, 10 \, - \, 2\,x \, \]

Därmed blir lådans volym \( V(x) \, = \, x \cdot y^2 \, \).

Eftersom det är den öppna lådans volym som ska maximeras är problemets målfunktion:

\[ \quad V(x) \, = \, x \cdot (10 \, - \, 2\,x)^2 \, \].

@@ Rad 1: / Rad 1: @@
-Vi inför beteckningen <math> \, y \, </math> för bassidan av den öppna lådan som ska byggas:
 [[Image: Ovn 356 Oppen lada_1_80_y.jpg]]
-Då kan problemets bivillkor formuleras så här:
+Från a) har vi problemets bivillkor:
 ::<math> y \, = \, 10 \, - \, 2\,x \, </math>
-eftersom kartongens sida är <math> \, 10 \; {\rm dm} \, </math> lång varav <math> \, 2\,x \, </math> skärs ut, så att <math> \, y \, </math> blir bassidan av den öppna lådan som ska byggas.
+Därmed blir lådans volym <math> V(x) \, = \, x \cdot y^2 \, </math>.
-Rektangelns andra sida  som är parallell till muren har längden:
-::<math> \, 9 \, - \, 2\,x \, </math>
-eftersom stängseln är <math> \, 9 \; {\rm m} \, </math> lång varav endast <math> \, 2\,x \, </math> går åt sidorna som är vinkelräta mot muren.
-Därmed blir rektangelns area <math> \, = \, x \cdot (9 \, - \, 2\,x) \, </math>
-Eftersom det är rektangelns area som ska maximeras är problemets målfunktion:
+Eftersom det är den öppna lådans volym som ska maximeras är problemets målfunktion:
-::<math> \, A(x) \, = \, x \cdot (9 \, - \, 2\,x) \, </math>
+::<math> \quad V(x) \, = \, x \cdot (10 \, - \, 2\,x)^2 \, </math>.