Skillnad mellan versioner av "3.4 Lösning 5"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 21: | Rad 21: | ||
# <math> f(x) \, </math> har i <math> \, x_1 = 0 \, </math> en terasspunkt pga <math> f\,'(0) = f\,''(0) = 0 </math> och <math> f\,'''(0) \neq 0 </math>. | # <math> f(x) \, </math> har i <math> \, x_1 = 0 \, </math> en terasspunkt pga <math> f\,'(0) = f\,''(0) = 0 </math> och <math> f\,'''(0) \neq 0 </math>. | ||
# <math> f(x) \, </math> har i <math> \, x_2 = 0,75 \, </math> en maximipunkt pga <math> f\,'(0,75) = 0 </math> och <math> f\,''(0,75) < 0 </math>. | # <math> f(x) \, </math> har i <math> \, x_2 = 0,75 \, </math> en maximipunkt pga <math> f\,'(0,75) = 0 </math> och <math> f\,''(0,75) < 0 </math>. | ||
| + | |||
| + | Att funktionen växer kring terasspunkten beror på att derivatan enligt grafen är positiv kring origo. | ||
Versionen från 23 januari 2015 kl. 10.33
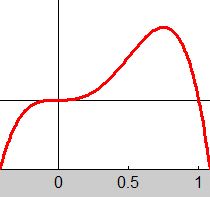
Derivatans graf visar att den har två nollställen:
- \[ x_1 = 0 \]
- \[ x_2 \approx 0,75 \]
Andraderivatans graf visar:
- \[ f\,''(0) = 0 \]
- \[ f\,''(0,75) < 0 \]
Tredje derivatans graf visar:
- \[ f\,'''(0) \neq 0 \]
Härav följer:
- \( f(x) \, \) har i \( \, x_1 = 0 \, \) en terasspunkt pga \( f\,'(0) = f\,''(0) = 0 \) och \( f\,'''(0) \neq 0 \).
- \( f(x) \, \) har i \( \, x_2 = 0,75 \, \) en maximipunkt pga \( f\,'(0,75) = 0 \) och \( f\,''(0,75) < 0 \).
Att funktionen växer kring terasspunkten beror på att derivatan enligt grafen är positiv kring origo.