Skillnad mellan versioner av "1.5 Övningar till Kontinuerliga och diskreta funktioner"
Taifun (Diskussion | bidrag) m (→Övning 5) |
Taifun (Diskussion | bidrag) m (→Övning 5) |
||
| Rad 86: | Rad 86: | ||
I teoridelen, [[1.5_Kontinuerliga_och_diskreta_funktioner#Exempel_3_Fibonaccis_problem|<strong><span style="color:blue">Exempel 3</span></strong>]], beräknades de 12 första fibonaccitalen med hjälp av [[1.5_Kontinuerliga_och_diskreta_funktioner#Fibonaccis_funktion|<strong><span style="color:blue">Fibonaccis funktion</span></strong>]]. | I teoridelen, [[1.5_Kontinuerliga_och_diskreta_funktioner#Exempel_3_Fibonaccis_problem|<strong><span style="color:blue">Exempel 3</span></strong>]], beräknades de 12 första fibonaccitalen med hjälp av [[1.5_Kontinuerliga_och_diskreta_funktioner#Fibonaccis_funktion|<strong><span style="color:blue">Fibonaccis funktion</span></strong>]]. | ||
| − | a) Använd samma funktion för att komplettera beräkningen med ytterligare 12 fibonaccital som följer efter de 12 första, dvs beräkna <math> F(13) - F(24)\, </math> för att slutligen kunna besvara frågan: Hur många kaninpar kommer att finnas | + | a) Använd samma funktion för att komplettera beräkningen med ytterligare 12 fibonaccital som följer efter de 12 första, dvs beräkna <math> F(13) - F(24)\, </math> för att slutligen kunna besvara frågan: Hur många kaninpar kommer att finnas om två år? |
b) Rita Fibonaccis diskreta funktion för de första 24 fibonaccitalen genom att komplettera [[1.5_Kontinuerliga_och_diskreta_funktioner#Grafen|<strong><span style="color:blue">grafen</span></strong>]] för de 12 första fibonaccitalen som visades i slutet av Exempel 3. | b) Rita Fibonaccis diskreta funktion för de första 24 fibonaccitalen genom att komplettera [[1.5_Kontinuerliga_och_diskreta_funktioner#Grafen|<strong><span style="color:blue">grafen</span></strong>]] för de 12 första fibonaccitalen som visades i slutet av Exempel 3. | ||
Versionen från 12 juli 2014 kl. 09.42
| <-- Förra avsnitt | Teori | Övningar | Fördjupning | Nästa avsnitt --> |
E-övningar: 1-5
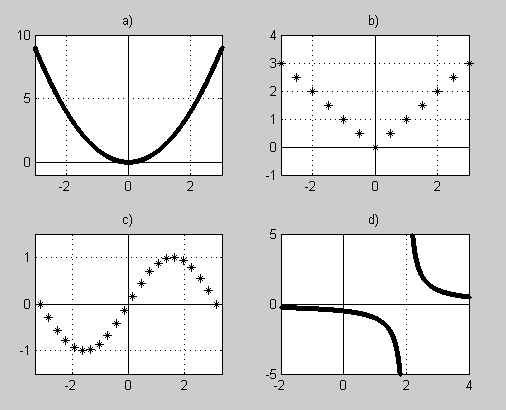
Övning 1
Bestäm för varje graf om den visar en diskret eller en kontinuerlig funktion.
Ange även om och i så fall för vilka \( x \, \) funktionerna har diskontinuiteter.
Motivera dina svar.
Övning 2
a) Rita grafen till den diskreta funktionen
- \[ y = x^2\, \]
vars definitionsmängd är alla heltal \( x\, \) mellan \( -5\, \) och \( 5\, \) dvs \( -5 \leq x \leq 5 \).
Undersök om din grafräknare kan rita diskreta funktioner. Om ja gör det, annars rita manuellt på rutat papper.
b) Rita med grafräknaren grafen till den kontinuerliga funktionen
- \[ y = x^2\, \]
vars definitionsmängd är alla reella tal \( x\, \) mellan \( -5\, \) och \( 5\, \) dvs \( -5 \leq x \leq 5 \).
Fundera själv vilka min- och max-värden du borde ange för räknarens display (WINDOW-knappen).
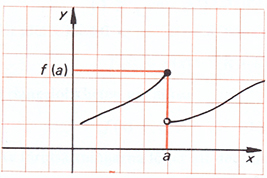
Övning 3
Anta att varje ruta i grafen nedan har längdenheten \( 1\, \).
a) Är funktionen \( f(x)\, \) diskret eller kontinuerlig?
b) Vilket värde kan du läsa av från grafen för funktionen \( f(x)\, \) för \( x = 4\, \)?
c) För vilka \( x\, \) är funktionen \( f(x)\, \) inte definierad i det ritade intervallet?
d) För vilka \( x\, \) är funktionen \( f(x)\, \) inte kontinuerlig i det ritade intervallet?
Motivera dina svar.
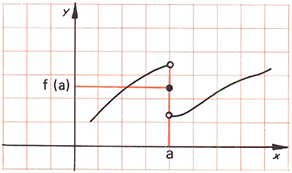
Övning 4
Anta att varje ruta i grafen nedan har längdenheten \( 1\, \).
a) Vilket värde kan du läsa av från grafen för funktionen \( f(x)\, \) för \( x = 4\, \)?
b) Är funktionen \( f(x)\, \) definierad för alla \( x\, \) i det ritade intervallet?
c) Är funktionen \( f(x)\, \) kontinuerlig för alla \( x\, \) i det ritade intervallet?
d) För vilka \( x\, \) är funktionen \( f(x)\, \) kontinuerlig och för vilka är den diskontinuerlig?.
Motivera dina svar.
Övning 5
I teoridelen, Exempel 3, beräknades de 12 första fibonaccitalen med hjälp av Fibonaccis funktion.
a) Använd samma funktion för att komplettera beräkningen med ytterligare 12 fibonaccital som följer efter de 12 första, dvs beräkna \( F(13) - F(24)\, \) för att slutligen kunna besvara frågan: Hur många kaninpar kommer att finnas om två år?
b) Rita Fibonaccis diskreta funktion för de första 24 fibonaccitalen genom att komplettera grafen för de 12 första fibonaccitalen som visades i slutet av Exempel 3.
 Hämtar...
Hämtar...