Skillnad mellan versioner av "1.5 Kontinuerliga och diskreta funktioner"

Från Mathonline
Hoppa till: navigering, sök
m (→‎Exempel 3 Fibonaccis funktion)
m
 
(549 mellanliggande versioner av samma användare visas inte)
Rad 1: Rad 1:
 +
__NOTOC__
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Selected tab|[[1.5 Kontinuerliga och diskreta funktioner|Teori]]}}
+
{{Not selected tab|[[1.4 Talet e och den naturliga logaritmen| <<&nbsp;&nbsp;Förra demoavsnitt]]}}
 +
{{Selected tab|[[1.5 Kontinuerliga och diskreta funktioner|Genomgång]]}}
 
{{Not selected tab|[[1.5 Övningar till Kontinuerliga och diskreta funktioner|Övningar]]}}
 
{{Not selected tab|[[1.5 Övningar till Kontinuerliga och diskreta funktioner|Övningar]]}}
−
{{Not selected tab|[[1.5 Repetitionsuppgifter till 1.1 - 1.4|Repetitionsuppgifter till 1.1 - 1.4]]}}
+
{{Not selected tab|[[1.5 Fördjupning till Kontinuerliga och diskreta funktioner|Fördjupning]]}}
−
{{Not selected tab|[[1.5 Internetlänkar till Kontinuerliga och diskreta funktioner|Internetlänkar]]}}
+
{{Not selected tab|[[1.6 Absolutbelopp|Nästa demoavsnitt&nbsp;&nbsp;>> ]]}}
 +
<!-- {{Not selected tab|[[2.1 Introduktion till derivata|Nästa demoavsnitt <math> \pmb{\to} </math>]]}} -->
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
  
 +
<big>
 +
I matematiken betyder <b><span style="color:red">diskret</span></b> åtskild, avgränsad eller separerad och är motsatsen till kontinuerlig.
  
−
[[Media: Lektion 8 Kontin. & diskreta funktioner Ruta.pdf|Lektion 8 Kontinuerliga & diskreta funktioner]]
+
Heltalen bildar en diskret mängd därför att de är avgränsade från sina "grannar" på tallinjen med ett helsteg. Det finns inget heltal mellan <math> \, 2 \, </math> och <math> \, 3 \, </math> och inte heller mellan de andra heltalen.
  
−
__TOC__
+
"Antal" är alltid heltal och därmed diskret. Därför är t.ex. "antal ägg" diskret: Det finns inga halva eller bråkdel ägg.
 +
</big>
  
−
== Exempel 1 Diskret prisfunktion efter antal ==
 
  
−
En torghandlare säljer ägg för 3 kr per styck.  
+
== <b><span style="color:#931136">Exempel 1 Diskret funktion</span></b> ==
 +
<div class="ovnA">
 +
<big>
 +
<table>
 +
<tr>
 +
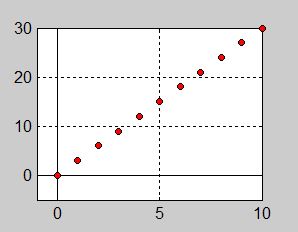
  <td>En torghandlare säljer ägg för <math> \, 3 </math> kr per styck.
  
−
a) Ställ upp en funktion som beskriver priset <math> y \, </math> kr för <math> x \, </math> st ägg.
+
<math> {\color{Red} 1} \; </math> ägg kostar <math> {\color{Red} 1} \cdot 3 \;{\rm kr,} </math>
  
−
b) Rita grafen till funktionen i a).
+
<math> {\color{Red} 2} \; </math> ägg kostar <math> {\color{Red} 2} \cdot 3 \;{\rm kr,} </math>
  
−
'''Lösning:'''
+
<math> {\color{Red} 3} \; </math> ägg kostar <math> {\color{Red} 3} \cdot 3 \;{\rm kr,} \qquad \cdots </math>
  
−
a) <math> {\color{White} x} {\color{Red} 1} \, </math> ägg kostar <math> {\color{Red} 1} \cdot 3 \;{\rm kr,} </math>
+
<math> {\color{Red} n} \; </math> ägg kostar <math> {\color{Red} n} \cdot 3 \;{\rm kr} </math> eller <math> 3\;{\color{Red} n} \;{\rm kr.} </math>
  
−
:<math> {\color{Red} 2} \, </math> ägg kostar <math> {\color{Red} 2} \cdot 3 \;{\rm kr,} </math>
+
Därför är prisfunktionen:
  
−
:<math> {\color{Red} 3} \, </math> ägg kostar <math> {\color{Red} 3} \cdot 3 \;{\rm kr,} </math>
+
<div class="smallBoxVariant"><math> y = 3\;{\color{Red} n} \, , \quad
 +
{\rm där } \quad {\color{Red} n}\,= {\rm {\color{Red} {heltal}}\,.} </math></div>
 +
</td>
 +
  <td> &nbsp;  &nbsp; &nbsp;  &nbsp; [[Image: Diskret_prisfunktion_agg.jpg]]</td>
 +
  <td> &nbsp;  &nbsp; &nbsp;  &nbsp; Grafen till prisfunktionen visar priset <math> y \, </math> i kr (vertikal axel)
  
−
:<math> {\color{White} x} \qquad \cdots </math>
+
&nbsp;  &nbsp; &nbsp;  &nbsp; som en funktion av <b><span style="color:red">antalet</span></b> <math> {\color{Red} n} \, </math> (horisontell axel).
  
−
:<math> {\color{Red} x} \, </math> ägg kostar <math> {\color{Red} x} \cdot 3 \;{\rm kr} </math> eller <math> 3\;{\color{Red} x} \;{\rm kr.} </math>
 
  
−
Därför är prisfunktionen:
+
&nbsp;  &nbsp; &nbsp;  &nbsp; Grafen till en diskret funktion ritas med <b><span style="color:red">separerade</span></b>
  
−
::<math> y = 3\;{\color{Red} x} </math>
+
&nbsp;  &nbsp; &nbsp;  &nbsp; <b><span style="color:red">punkter</span></b> och inte med en genomdragen linje.
  
−
b) Grafen till Funktionen <math> y = 3\;{\color{Red} x} </math> visar priset <math> y \, </math> som en funktion av antalet <math> x \, </math>:
 
  
−
[[Image: Diskret prisfunktion ägg 70.jpg]]
+
&nbsp;  &nbsp; &nbsp;  &nbsp; För att rita en diskret funktions graf måste man
  
−
Funktionen <math> y = 3\;{\color{Red} x} </math> med <math> {\color{Red} x} \, </math> <strong><span style="color:red"> = antal ägg </span></strong> är ett exempel på en <strong><span style="color:red">diskret</span></strong> funktion.  
+
&nbsp;  &nbsp; &nbsp;  &nbsp; lyfta pennan.
 +
  </td>
 +
</tr>
 +
</table>
 +
<math> \quad\; y \, </math> är priset i kr. <math> \quad\; \color{Red} n \, </math> är antalet ägg.
  
−
I matematiken betyder <strong><span style="color:red">diskret</span></strong> distinkt dvs avgränsat, separerat och är motsatsen till kontinuerlig. För att rita en diskret funktions graf måste man lyfta pennan minst en gång. Heltalen bildar en diskret mängd därför att de är avgränsade till sina "grannar" på tallinjen med ett helsteg. Det finns inget heltal mellan 2 och 3 osv. "Antal" är alltid heltal och därmed diskret. Samma gäller förstås för "antal ägg". Det finns inga halva eller bråkdel ägg.
+
<math> y = 3\;{\color{Red} n} </math> är en <div class="smallBox"><b><span style="color:red">diskret funktion</span></b></div> &nbsp;&nbsp; därför att dess <b><span style="color:red">definitionsmängd</span></b> är en <div class="smallBox"><b><span style="color:red">diskret mängd</span></b></div> &nbsp;&nbsp; nämligen alla <b><span style="color:red"> heltal </span></b> <math> {\color{Red} n} \geq 0\, </math>.  
 +
</big>
 +
</div>
  
−
Funktionen <math> y = 3\;{\color{Red} x} </math> är diskret därför att dess definitionsmängd: alla <math> {\color{Red} x} \geq 0\, </math> med <math> {\color{Red} x} \, </math> <strong><span style="color:red"> = antal ägg </span></strong> är en diskret mängd. Därför är dess graf ritad med separerade prickar och inte med en genomdragen linje.
 
  
 +
<big>
 +
I matematiken betyder <b><span style="color:red">kontinuerlig</span></b> sammanhängande och är motsatsen till diskret.
  
−
== Exempel 2 Kontinuerlig prisfunktion efter vikt ==
+
De rationella och reella talen är kontinuerliga mängder därför att mellan två sådana tal - hur nära varandra de än mår vara - finns alltid oändligt många andra tal.
  
−
En annan torghandlare säljer ris för 30 kr per kilo.  
+
En mängd vätska t.ex. är kontinuerlig: Det finns halva eller alla möjliga bråkdelar av mängden.
 +
</big>
  
−
a) Ställ upp en funktion som beskriver priset <math> y \, </math> kr för <math> x \, </math> kilo.
 
  
−
b) Rita grafen till funktionen i a).
+
== <b><span style="color:#931136">Exempel 2 Kontinuerlig funktion</span></b> ==
 +
<div class="ovnC">
 +
<big>
 +
<table>
 +
<tr>
 +
  <td>
 +
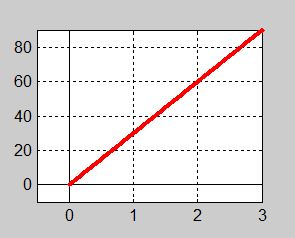
En annan torghandlare säljer färskpressad
  
−
'''Lösning:'''
+
granatäppeljuice för <math> \, 30 </math> kr per liter.
  
−
a) <math> {\color{White} x} {\color{Red} 1} \, </math> kg ris kostar <math> {\color{Red} 1} \cdot 30 \;{\rm kr,} </math>
+
Av samma anledning som i <b><span style="color:#931136">Exempel 1</span></b> är
  
−
:<math> {\color{Red} 2} \, </math> kg ris kostar <math> {\color{Red} 2} \cdot 30 \;{\rm kr,} </math>
+
prisfunktionen här:
  
−
:<math> {\color{Red} 3} \, </math> kg ris kostar <math> {\color{Red} 3} \cdot 30 \;{\rm kr,} </math>
+
<div class="smallBoxVariant"><math> y = 30\;{\color{Red} x} \, , \quad
 +
{\rm där } \quad {\color{Red} x}\,= {\rm {\color{Red} {reellt\;tal}}\,.} </math>
 +
</div>
 +
<math> \quad\; y \, </math> är priset i kr. <math> \quad\;\;\; \color{Red} x \, </math> är mängden i liter.
  
−
:<math> {\color{White} x} \qquad \cdots </math>
+
<math> y = 30\;{\color{Red} x} </math> är en <div class="smallBox"><b><span style="color:red">kontinuerlig funktion</span></b></div>
 +
</td>
 +
  <td> &nbsp;  &nbsp; &nbsp;  &nbsp; [[Image: Kontinuerlig_prisfunktion_ris.jpg]]</td>
 +
  <td> &nbsp;  &nbsp; &nbsp;  &nbsp; Grafen till Funktionen <math> y = 30\;{\color{Red} x} </math> visar priset <math> y \, </math>  
  
−
:<math> {\color{Red} x} \, </math> kg ris kostar <math> {\color{Red} x} \cdot 30 \;{\rm kr} </math> eller <math> 30\;{\color{Red} x} \;{\rm kr.} </math>
+
&nbsp;  &nbsp; &nbsp;  &nbsp; som en funktion av <b><span style="color:red">mängden</span></b> <math> {\color{Red} x} </math> (i liter).
  
−
Därför är prisfunktionen:
 
  
−
::<math> y = 30\;{\color{Red} x} </math>
+
&nbsp; &nbsp; &nbsp;  &nbsp; Grafen till en kontinuerlig funktion ritas med en
  
−
b) Grafen till Funktionen <math> y = 30\;{\color{Red} x} </math> visar priset <math> y \, </math> som en funktion av vikten <math> x \, </math>:
+
&nbsp;  &nbsp; &nbsp;  &nbsp; <b><span style="color:red">genomdragen linje</span></b> och inte med separerade punkter.
  
−
[[Image: Kontinuerlig prisfunktion ägg 70.jpg]]
 
  
−
Funktionen <math> y = 30\;{\color{Red} x} </math> med <math> {\color{Red} x} \, </math> <strong><span style="color:red"> = kg ris </span></strong> är ett exempel på en <strong><span style="color:red">kontinuerlig</span></strong> funktion.
+
&nbsp; &nbsp; &nbsp;  &nbsp; En kontinuerlig funktions graf kan man rita
  
−
I matematiken betyder <strong><span style="color:red">kontinuerlig</span></strong> sammanhängande och är motsatsen till diskret. En kontinuerlig funktions graf kan man rita utan att lyfta pennan. De rationella och reella talen är kontinuerliga mängder därför att mellan två sådana tal - hur nära varandra de än mår vara - finns alltid oändligt många andra tal.  
+
&nbsp;  &nbsp; &nbsp;  &nbsp; utan att lyfta pennan.
 +
  </td>
 +
</tr>
 +
</table>
 +
därför att dess <b><span style="color:red">definitionsmängd</span></b> är en <div class="smallBox"><b><span style="color:red">kontinuerlig mängd</span></b></div>&nbsp;&nbsp;&nbsp;&nbsp;nämligen alla <b><span style="color:red"> reella tal</span></b> <math> {\color{Red} x} \geq 0\, </math>.
 +
</big>
 +
</div>
  
−
Funktionen <math> y = 30\;{\color{Red} x} </math> är kontinuerlig därför att dess definitionsmängd: alla <math> {\color{Red} x} \geq 0\, </math> med <math> {\color{Red} x} \, </math> <strong><span style="color:red"> = kg ris </span></strong> är en kontinuerlig mängd. Därför är dess graf ritad med en genomdragen linje, utan att lyfta pennan.
+
<div class="tolv"> <!-- tolv2 -->
 +
Kontinuerliga funktioner används ofta som matematiska modeller för att beskriva verkligheten. Men i vissa fall föredrar man diskreta modeller som studeras i en speciell disciplin
  
−
'''Anmärkning 1:''' I exemplet ovan har man försummat att ett riskorn väger ca. 0,02 g. Eftersom man inte kan dela ett riskorn kan man - rent teoretiskt - hävda att funktionen i exemplet också är diskret. Priset växer nämligen med ett diskret steg på 0,02 g * 3 ören/g = 0,06 ören. Men i praktiken kan man kanske förlåta denna försummelse.
+
som heter [http://sv.wikipedia.org/wiki/Diskret_matematik <b><span style="color:blue">Diskret matematik</span></b>]. Talteori, mängdlära  och kombinatorik är typiska ämnen i Diskret matematik som behandlas i Matte 5.
 +
</div>
  
−
'''Anmärkning 2:''' I verkligheten finns det - exakt talat - inga kontinuerliga mängder, vilket visar betydelsen av diskreta funktioner. Kontinuitet är en matematisk abstraktion som endast förekommer i talmängder eller andra matematiska objekt. Kontinuerliga funktioner är matematiska modeller som man i regel använder för att beskriva verkligheten. Men i vissa fall föredrar man diskreta modeller. Sådana modeller studeras i en speciell disciplin av matematiken som heter [http://sv.wikipedia.org/wiki/Diskret_matematik <strong><span style="color:red">Diskret matematik</span></strong>].
 
  
 +
== <b><span style="color:#931136">[[Fibonaccis talföljd|<span style="color:blue">Exempel 3 Fibonaccis talföljd</span>]] </span></b> ==
  
−
== Exempel 3 Fibonaccis funktion ==
+
<br>
  
−
Ett exempel på problem som med fördel kan modelleras med diskreta funktioner är följande uppgift som den italienske matematikern [http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibBio.html <strong><span style="color:blue">Leonardo Pisano Fibonacci</span></strong>] år 1202 formulerade i sin bok [http://liberabaci.blogspot.se/ <strong><span style="color:blue">Liber abaci (Boken om räknekonsten)</span></strong>]. Den handlar om kaniners fortplantning:
 
  
−
[[Image: Fibonacci problem 80.jpg]]
 
  
−
Om vi följer uppgiftens lydelse och räknar fram de första månaderna får vi följande tabell:
 
−
::::::{| class="wikitable"
 
−
|-
 
−
! Antal månader || Antal kaninpar
 
−
|-
 
−
| align=center| <math> 1\, </math> ||align=center| <math> 1\, </math>
 
−
|-
 
−
| align=center| <math> 2\, </math> ||align=center| <math> 1\, </math>
 
−
|-
 
−
| align=center| <math> 3\, </math> ||align=center| <math> 2\, </math>
 
−
|-
 
−
| align=center| <math> 4\, </math> ||align=center| <math> 3\, </math>
 
−
|-
 
−
| align=center| <math> 5\, </math> ||align=center| <math> 5\, </math>
 
−
|-
 
−
| align=center| <math> 6\, </math> ||align=center| <math> 8\, </math>
 
−
|-
 
−
| align=center| <math> 7\, </math> ||align=center| <math> 13\, </math>
 
−
|-
 
−
| align=center| <math> 8\, </math> ||align=center| <math> 21\, </math>
 
−
|-
 
−
| align=center| <math> \cdots </math> ||align=center| <math> \cdots </math>
 
−
|}
 
−
Antal månader 1 2 3 4 5 6 7 8 …
 
−
Antal kaninpar 1 1 2 3 5 8 13 21 …
 
  
−
Det uppstår en talföljd i den andra raden av tabellen som kallas Fibonaccis talföljd eller kort fibonaccitalen. Så här uppstår de:
 
  
−
De två första månaderna finns det 1 kaninpar. De föder sitt första barnpar först efter 2 må¬nader dvs i månad nr 3, varför det finns 2 kaninpar i månad 3. I månad 4 föder det första paret sitt andra barnpar, varför det finns 3 par i månad 4. I månad 5 föder det första paret sitt tredje barnpar, men även deras första barnpar föder ett nytt par, ef¬ter-som det har gått 2 månader sedan deras födelse. Därför finns det 5 par i må¬nad 5. Osv. …
 
  
−
Praktiskt taget blir det allt svårare att hålla reda på antalet kaninpar när antalet månader växer. Man måste kanske rita någon sorts diagram och anteckna allt från månad till må¬nad. En utväg ur dilemmat vore att upptäcka ett mönster, en struktur, t.ex. ett samband mellan antal månader och kaninpar, en slags laglighet i bildandet av fibonaccitalen som kan beskrivas i form av en algoritm för att sedan kunna skrivas som program. Undersö¬ker man tabellen noga kan man se följande enkelt mönster: Summan av två på varan¬dra följande fibonaccital ger nästa fibonaccital. Kolla själv! Men hur kav vi beskriva detta mönster?
 
  
−
Vi inför beteckningarna: n  = Antalet månader
+
== <b><span style="color:#931136">Internetlänkar</span></b> ==
−
Fn = Antalet kaninpar i månaden n
+
 
 +
http://www.youtube.com/watch?v=SKRjz2aTqCY
 +
 
 +
http://www.youtube.com/watch?v=cvnG0YWPLjQ
 +
 
 +
http://www.sigma8.se/dokument/TabyFriskola_Amnesrapport_OK_2012.pdf
 +
 
 +
http://www03.edu.fi/svenska/oppimateriaalit/arkimatematiikkaa/fibona.html
 +
 
 +
http://paranormal.se/topic/det_gyllene_snittet.html
 +
 
 +
http://www.math.fau.edu/MathCircle_at_FAU/MC130713Problems.pdf
 +
 
 +
 
  
−
Mönstret som vi upptäckte ovan kan vi nu beskriva så här:
 
  
−
F1 = 1, F2 = 1
 
−
Fn = Fn-1 + Fn-2 för n = 3, 4, 5, …
 
  
−
Den första raden säger att de första två fibonacci¬talen är 1 och 1. Den andra raden säger att det n-te fibonacci¬talet är summan av de två föregående, vilket är bara en annan for¬mulering av samma mönster vi upptäckte i tabellen. Formeln ovan kallas Fibonaccis re¬kursionsformel. Men vad är det rekursiva i denna formel? I en vanlig, icke-rekursiv for¬mel står den sökta storheten vänster om likhetstecknet och alla givna storheter höger om likhetstecknet. Men här står den sökta storheten, fibonacci¬talen, på båda sidor likhets¬tecknet, fast för olika månader, för olika parametrar så att säga. För att beräkna ett fibo¬nacci¬tal måste man känna till de två föregående. Men eftersom vi har de två första F1 och F2, s.k. startvärden, kan vi beräkna alla andra successivt utgående från dessa start¬värden. Att det sökta står på båda sidor likhetstecknet är alltså det rekursiva, vilket, när vi kodar formeln, resulterar i en metod som anropar sig själv, fast med olika parametrar.
 
  
  
  
−
:
+
[[Matte:Copyrights|Copyright]] © 2021 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved.

Nuvarande version från 1 juli 2024 kl. 11.25

        <<  Förra demoavsnitt          Genomgång          Övningar          Fördjupning          Nästa demoavsnitt  >>      


I matematiken betyder diskret åtskild, avgränsad eller separerad och är motsatsen till kontinuerlig.

Heltalen bildar en diskret mängd därför att de är avgränsade från sina "grannar" på tallinjen med ett helsteg. Det finns inget heltal mellan \( \, 2 \, \) och \( \, 3 \, \) och inte heller mellan de andra heltalen.

"Antal" är alltid heltal och därmed diskret. Därför är t.ex. "antal ägg" diskret: Det finns inga halva eller bråkdel ägg.


Exempel 1 Diskret funktion

En torghandlare säljer ägg för \( \, 3 \) kr per styck.

\( {\color{Red} 1} \; \) ägg kostar \( {\color{Red} 1} \cdot 3 \;{\rm kr,} \)

\( {\color{Red} 2} \; \) ägg kostar \( {\color{Red} 2} \cdot 3 \;{\rm kr,} \)

\( {\color{Red} 3} \; \) ägg kostar \( {\color{Red} 3} \cdot 3 \;{\rm kr,} \qquad \cdots \)

\( {\color{Red} n} \; \) ägg kostar \( {\color{Red} n} \cdot 3 \;{\rm kr} \) eller \( 3\;{\color{Red} n} \;{\rm kr.} \)

Därför är prisfunktionen:

\( y = 3\;{\color{Red} n} \, , \quad {\rm där } \quad {\color{Red} n}\,= {\rm {\color{Red} {heltal}}\,.} \)
         Diskret prisfunktion agg.jpg         Grafen till prisfunktionen visar priset \( y \, \) i kr (vertikal axel)

        som en funktion av antalet \( {\color{Red} n} \, \) (horisontell axel).


        Grafen till en diskret funktion ritas med separerade

        punkter och inte med en genomdragen linje.


        För att rita en diskret funktions graf måste man

        lyfta pennan.

\( \quad\; y \, \) är priset i kr. \( \quad\; \color{Red} n \, \) är antalet ägg.

\( y = 3\;{\color{Red} n} \) är en
diskret funktion
   därför att dess definitionsmängd är en
diskret mängd
   nämligen alla heltal \( {\color{Red} n} \geq 0\, \).


I matematiken betyder kontinuerlig sammanhängande och är motsatsen till diskret.

De rationella och reella talen är kontinuerliga mängder därför att mellan två sådana tal - hur nära varandra de än mår vara - finns alltid oändligt många andra tal.

En mängd vätska t.ex. är kontinuerlig: Det finns halva eller alla möjliga bråkdelar av mängden.


Exempel 2 Kontinuerlig funktion

En annan torghandlare säljer färskpressad

granatäppeljuice för \( \, 30 \) kr per liter.

Av samma anledning som i Exempel 1 är

prisfunktionen här:

\( y = 30\;{\color{Red} x} \, , \quad {\rm där } \quad {\color{Red} x}\,= {\rm {\color{Red} {reellt\;tal}}\,.} \)

\( \quad\; y \, \) är priset i kr. \( \quad\;\;\; \color{Red} x \, \) är mängden i liter.

\( y = 30\;{\color{Red} x} \) är en
kontinuerlig funktion
         Kontinuerlig prisfunktion ris.jpg         Grafen till Funktionen \( y = 30\;{\color{Red} x} \) visar priset \( y \, \)

        som en funktion av mängden \( {\color{Red} x} \) (i liter).


        Grafen till en kontinuerlig funktion ritas med en

        genomdragen linje och inte med separerade punkter.


        En kontinuerlig funktions graf kan man rita

        utan att lyfta pennan.

därför att dess definitionsmängd är en
kontinuerlig mängd
    nämligen alla reella tal \( {\color{Red} x} \geq 0\, \).

Kontinuerliga funktioner används ofta som matematiska modeller för att beskriva verkligheten. Men i vissa fall föredrar man diskreta modeller som studeras i en speciell disciplin

som heter Diskret matematik. Talteori, mängdlära och kombinatorik är typiska ämnen i Diskret matematik som behandlas i Matte 5.


Exempel 3 Fibonaccis talföljd





Internetlänkar

http://www.youtube.com/watch?v=SKRjz2aTqCY

http://www.youtube.com/watch?v=cvnG0YWPLjQ

http://www.sigma8.se/dokument/TabyFriskola_Amnesrapport_OK_2012.pdf

http://www03.edu.fi/svenska/oppimateriaalit/arkimatematiikkaa/fibona.html

http://paranormal.se/topic/det_gyllene_snittet.html

http://www.math.fau.edu/MathCircle_at_FAU/MC130713Problems.pdf





Copyright © 2021 TechPages AB. All Rights Reserved.

Hämtad från "https://minidemo.mathonline.se/index.php?title=1.5_Kontinuerliga_och_diskreta_funktioner&oldid=29389"