Skillnad mellan versioner av "1.1 Lösning 4b"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (En mellanliggande version av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
Graferna till <math> y_1 = \sqrt{x^2 + 1} </math> och <math> \displaystyle y_2 = x - 3 </math> ritade i samma koordinatsystem: | Graferna till <math> y_1 = \sqrt{x^2 + 1} </math> och <math> \displaystyle y_2 = x - 3 </math> ritade i samma koordinatsystem: | ||
| − | [[Image: | + | [[Image: Rotekv_Övn_4bR.jpg]] |
| − | Bilden visar kurvan <math> y_1 = \sqrt{x^2 + 1} </math> (blå) och linjen <math> \displaystyle y_2 = x - 3 </math> (grön) inte skär varandra. Dvs de har ingen gemensam punkt där deras funktionsvärden överensstämmer. | + | Bilden visar att kurvan <math> y_1 = \sqrt{x^2 + 1} </math> (blå) och linjen <math> \displaystyle y_2 = x - 3 </math> (grön) inte skär varandra. Dvs de har ingen gemensam punkt där deras funktionsvärden överensstämmer. |
Detta bekräftar att ekvationen | Detta bekräftar att ekvationen | ||
Nuvarande version från 21 november 2010 kl. 14.05
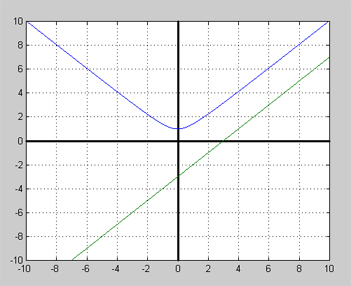
Graferna till y1=√x2+1 och y2=x−3 ritade i samma koordinatsystem:
Bilden visar att kurvan y1=√x2+1 (blå) och linjen y2=x−3 (grön) inte skär varandra. Dvs de har ingen gemensam punkt där deras funktionsvärden överensstämmer.
Detta bekräftar att ekvationen
√x2+1=x−3
saknar lösning vilket visades i lösningen till övning 4a.
