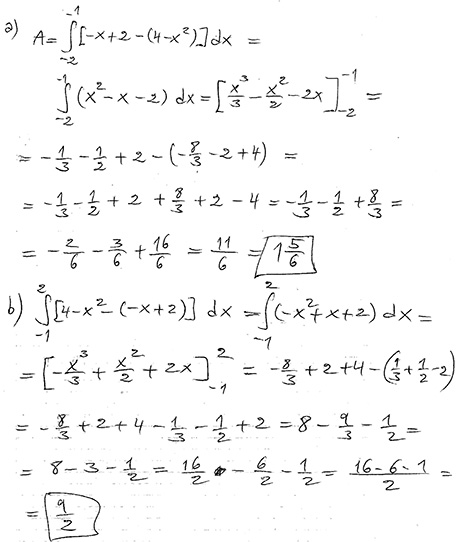Skillnad mellan versioner av "Kapitel 4 Integraler"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (En mellanliggande version av samma användare visas inte) | |||
| Rad 3: | Rad 3: | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
{{Not selected tab|[[Matte 3 Kapitel 3 Användning av derivata| << Förra kapitel]]}} | {{Not selected tab|[[Matte 3 Kapitel 3 Användning av derivata| << Förra kapitel]]}} | ||
| − | {{Selected tab|[[Kapitel 4 Integraler| | + | {{Selected tab|[[Kapitel 4 Integraler|Genomgångar]]}} |
{{Not selected tab|[[Media: Formelsamling NP Ma3 Integ.pdf|Formelsamling Integraler]]}} | {{Not selected tab|[[Media: Formelsamling NP Ma3 Integ.pdf|Formelsamling Integraler]]}} | ||
{{Not selected tab|[[Matte 3c Planering|Planering Matte 3c]]}} | {{Not selected tab|[[Matte 3c Planering|Planering Matte 3c]]}} | ||
| Rad 13: | Rad 13: | ||
F.o.m. detta kapitel finns kursens övningar inte på webben (pga tidsbrist). Därför: | F.o.m. detta kapitel finns kursens övningar inte på webben (pga tidsbrist). Därför: | ||
| − | Läs igenom genomgångarna här, men | + | Läs igenom genomgångarna här, men använd för övningarna boken <i>Matematik 5000</i>. |
== <b><span style="color:#931136">Utdrag ur planeringen:</span></b> == | == <b><span style="color:#931136">Utdrag ur planeringen:</span></b> == | ||
Nuvarande version från 14 februari 2018 kl. 12.24
| << Förra kapitel | Genomgångar | Formelsamling Integraler | Planering Matte 3c |
F.o.m. detta kapitel finns kursens övningar inte på webben (pga tidsbrist). Därför:
Läs igenom genomgångarna här, men använd för övningarna boken Matematik 5000.
Utdrag ur planeringen:
Lektion 29: 4.1 Primitiva funktioner \( \qquad\qquad\qquad\;\; \) Övningar: Boken, sid 175
Hittills: En funktion är given. Vi söker funktionens derivata. Nu vänder vi på steken och ställer upp det omvända problemet:
Nu:OBS! Byte av beteckning:
\( \; f\,(x) \, \) är inte längre den ursprungliga funktionen utan en känd derivata av en okänd funktion som vi kallar för \( \, F\,(x) \, \).
Exempel 1:
Givet: \( \quad\;\; f\,(x) \, = \, 2\,x \, = \, \) Derivatan av någon funktion
Sökt: \( \quad\;\;\, F(x) \quad \) så att \( \quad F\,'(x) = 2\,x \)
Lösning: \( \;\; F(x) = \boxed{\textstyle x\,^2 \, + C\,} \, , \;\; C={\rm const.} \)
Kontroll: \( \;\; F\,'(x) = 2\,x + 0 \, = \, 2\,x \, = \, f\,(x) \)
Att hitta en primitiv funktion kallas för integration.\( \qquad\;\;\, \) Primitiv funktion = "Anti"derivata
Exempel 2: Givet: \( \quad\;\; f\,(x) \, = \, x\,^3 + 5 \, = \, \) Derivatan av någon funktion Sökt: \( \quad\;\;\, F(x) \quad \) så att \( \quad F\,'(x) = x\,^3 + 5 \) Lösning: \( \;\; F(x) = \boxed{\textstyle \frac{1}{4} x\,^4 + 5 \, x + C\,} \, , \;\; C={\rm const.} \) Kontroll: \( \;\; F\,'(x) = \frac{4}{4} x\,^3 + 5 + 0 \, = \, x\,^3 + 5 \, = \, f\,(x) \) |
\( \quad \) | Allmän definition: Givet: \( \quad f\,(x) \) Sökt: \( \quad \) En funktion \( \;\; F\,(x) \;\; \) så att: \( \qquad\qquad\quad\; \boxed{F\,'\,(x) = f\,(x)} \) Funktionen \( \, F\,(x) \, \) kallas för primitiv funktion. |
- Integration är deriveringens inversa (omvända) operation. Därför:
- Integrationsregler för olika funktionstyper följer genom att vända om deriveringsreglerna. T.ex.:
Integrationsregeln för en potens: Om \( f(x) = x\,^n \qquad {\rm där} \qquad\, n = {\rm const.} \neq -1\) då \(\; F(x) = \boxed{\frac{x\,^{n+1}}{n+1} \, + \, C\;} \;, C = \) integrationskonstanten |
\( \quad \) |
Exempel: För \( \, f(x) \, = \, x^4 \; \) blir den primitiva funktionen:
|
- Bevis: \( \, F\,'(x) = \displaystyle \frac{(n+1) \, x\,^{n+1-1}}{n+1} \, + \, 0 \, = \, \frac{(n+1) \, x\,^{n}}{n+1} = x\,^n = f\,(x) \qquad \) Exempel: \( \;\; F\,'(x) \, = \, \displaystyle \frac{5}{5} \, x\,^4 \, + \, 0 \, = \, x\,^4 \, = \, f\,(x) \qquad \)
- Regeln ovan gäller inte bara för positiva \( \, n \, \) utan även för negativa (undantaget \( -1 \)) och rationella exponenter.
- Ytterligare regler om primitiva funktioner anges senare.
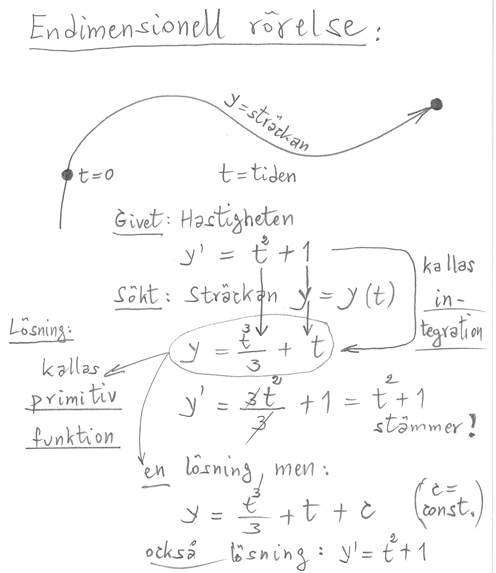
Fysikalisk tolkning:
| \( \quad \) |  |
\( \quad \) Hastighetsmätaren deriverar. \( \;\; \)
|
\( \quad \)  |
Integration är den inversa operationen till derivering. \( \quad \) Primitiv funktion = "Anti"derivata
Derivata Integral Fysikalisk tolkning: Hastighet Sträcka Geometrisk tolkning: Kurvans lutning Area under kurvan Matematisk tolkning: Limes av differenskvot Limes av oändlig summa
Integrationskonstanten \( \, C \, \):
Pga \( \, C={\rm const.} \, \) finns det alltid oändligt många primitiva funktioner till en given funktion.
För att få endast en primitiv funktion \( \, F(x) \, \) ställs vissa krav på \( \, F(x) \, \) som kallas för villkor,
i fysiken: begynnelsevillkor. Villkoren används för att bestämma integrationskonstanten \( \, C \, \). \( \; {\bf {\color{Red} {\downarrow}}} \)
Lektion 30: 4.2 Primitiva funktioner med villkor \( \qquad\qquad\qquad\;\; \) Övningar: Boken, sid 177
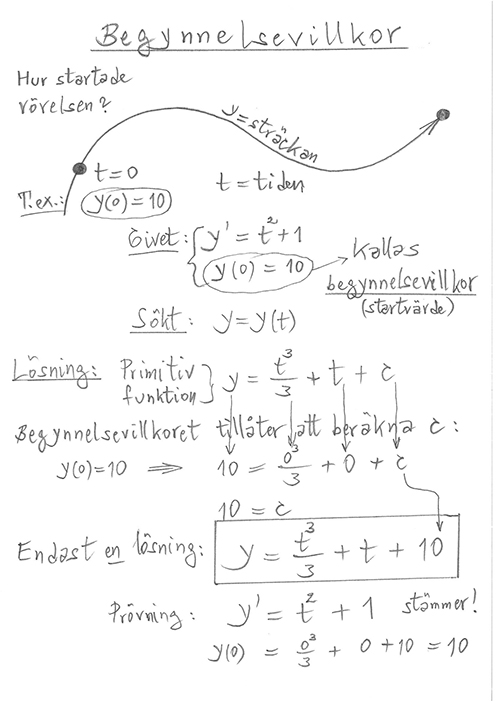
I fysikaliska tillämpningar är den typiska formen av villkor begynnelsevillkor. Frågan är:
Vad gällde i början, dvs vilket vägmärke passerades vid \( \, t = 0 \, \). Eller: Vad visade trippmätaren vid \( \, t = 0 \, \)?
Problemet ovan kallas även för en differentialekvation med begynnelsevillkor som kommer att behandlas i Matte 4 och 5.
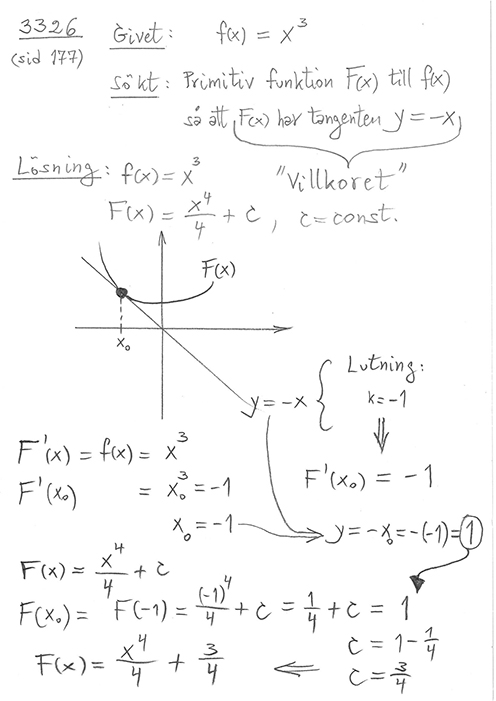
Geometriskt exempel på primitiv funktion med en annan typ av villkor:
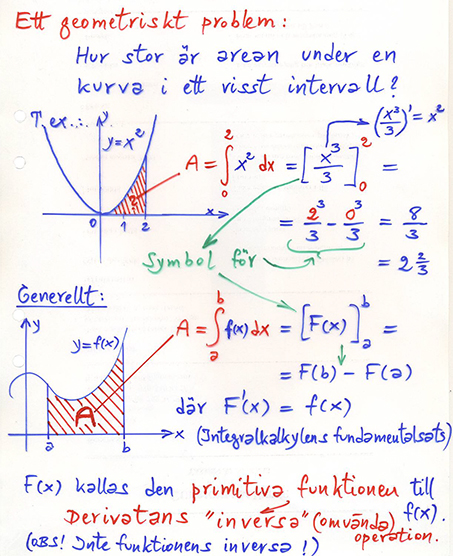
Lektion 31: 4.3 Integral som area under kurvan \( \qquad\qquad\qquad\;\; \) Övningar: Boken, sid 180
\( \, a \, \) och \( \, b \, \) kallas för integrationsgränser och ersätter integrationskonstanten \( \, C \, \).
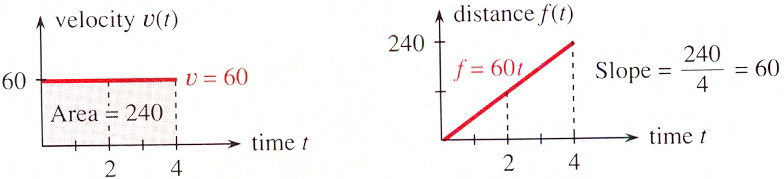
Fysikaliskt ex. på "Area under kurvan" : \( \quad \) Likformig rörelse med konstant hastighet 60 km/h
- \[ \text{Area} \; = \; \int\limits_0^4 {\color{Red} {60}} \; dt \; = \; \left[ \, {\color{Red} {60\,t}} \, \right]_0^4 \; = \; 60\cdot4 \, - \, 60\cdot0 \; = \; 240 \]
\( \qquad\; \)I exemplet: \( \quad \) Kör man med med \( \, 60 \, \) km/h i \( \, 4 \, \) timmar har man kört \( \, 60 \cdot 4 = 240 \, \) km.
\( \qquad\; \)Generellt:
Integralen över hastigheten = Arean under hastighetskurvan = Sträckan.
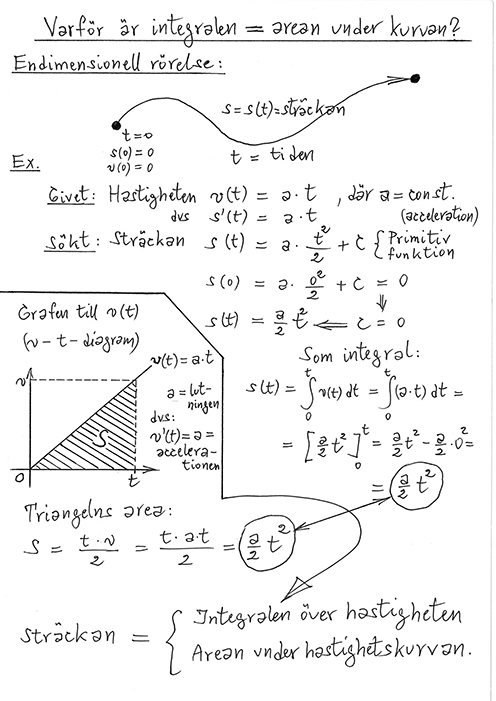
Rörelse med variabel hastighet (konstant acceleration):
Lektion 32: 4.4 Beräkning av integraler \( \qquad\qquad\qquad\;\; \) Övningar: Boken, sid 185
När en integral har integrationsgränser finns inga villkor med i uppgiften, eftersom de är inbakade i integrationsgränserna, se exemplen ovan.
En sådan integral kallas för bestämd integral. Dess resultat är ett tal.
En integral utan integrationsgränser kallas för obestämd integral.
En obestämd integrals resultat är inte ett tal, utan oändligt många primitiva funktioner.
För att entydigt bestämma endast en primitiv funktion måste ett villkor vara med.
Fattas villkoret måste alltid en integrationskonstant \( \, C \, \) adderas.
Integrationsregler för exponentialfunktioner
Om \( \; f(x) \, = \; e\,^{k\,x} \qquad {\rm där} \qquad\, k = {\rm const.} \) då är den primitiva funktionen \( \;\; F(x) \, = \, \boxed{\frac{e\,^{k\,x}}{k} \, + \, C\;} \; \) Om \( \; f(x) \, = \; a\,^{k\,x} \qquad {\rm där} \qquad\, a, k = {\rm const.} \) då är den primitiva funktionen \( \;\; F(x) \, = \, \boxed{\frac{a\,^{k\,x}}{k\,\ln a} \, + \, C\;} \; \)
|
\( \quad \) |
Exempel: Om \( \, f(x) \, = \, e\,^{4x} \; \) då är den primitiva funktionen:
Om \( \, f(x) \, = \, 2\,^{3x} \; \) då är den primitiva funktionen:
|
Lektion 33: 4.5 Användning av integraler \( \qquad\qquad\qquad\;\; \) Övningar: Boken, sid 188-90
Fysikaliskt exempel:
\( \quad \)En fallskärmshoppare faller fritt utan att öppna fallskärmen med hastigheten:
\( \qquad\qquad\qquad\qquad v(t) = 80\,(1 - 0,88\,^t) \)
där \( \, t = \, \) tiden i sek. Hur långt har hopparen fallit när \( \, v = 40 \, \) m/s ?
Fysikalisk tolkning: \( \; \)
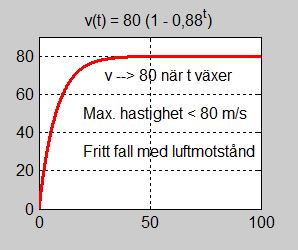
| \( \quad \) | Vi ritar grafen till \( \, v(t) \, \) och konstaterar att det finns en maximal hastighet
\( v_{max} = 80 \) m/s som hopparen inte kan överskrida. Algebraiskt: \( v_{max} \, = \, \displaystyle \lim_{t \to \infty}\,{(80\,(1 - 0,88\,^t))} \, = \, \lim_{t \to \infty}\,{(80 - 80\cdot0,88\,^t)} \, = \, 80 \, \), eftersom \( \qquad\;\; \displaystyle \lim_{t \to \infty}\,{(80\cdot0,88\,^t)} \, = \, 0 \quad \) pga \( \quad 0,88 \, < \, 1 \; \). När \( v \, \approx \, v_{max} = \, 80 \) m/s har vi likformig rörelse med konstant hastighet. Enligt Newtons fösta lag "Ett föremål är i vila eller rör sig med konstant hastighet, om och endast om summan av alla krafter \( \, = 0 \)" måste gälla: Luftmotstånd \( \, \approx \, \) Gravitation \( \quad \Rightarrow \quad \)Fritt fall med luftmotstånd
|
\( \;\;\; \) |  |
Uppgiften: Givet: \( \, s'(t) \, = \, v(t) \, = \, 80\,(1 - 0,88\,^t) \)
\( \qquad\qquad\qquad\quad\;\;\, \) Begynnelsevillkor: \( \, s(0) \, = \, 0 \)
\( \qquad\qquad\quad \) Sökt: \( \;\; s(t_1) \, \), där \( \; v(t_1) \, = \, 40 \, \) m/s
Lösningen:
Ekonomiskt exempel: "Marginal"kostnad som (given) derivata av kostnadsfunktionen (sökt integral).
Jfr. med "marginal"skatt \( \, = \, \) (sökt) derivata av skatten som en (given) funktion av lönen.
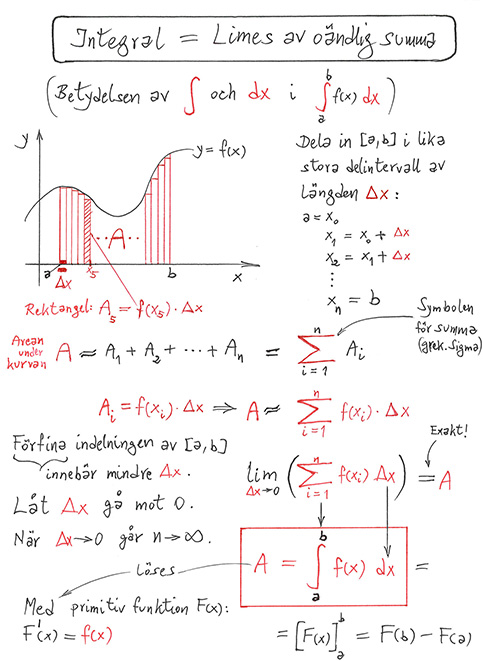
Appendix: Integral som limes av oändlig summa
Copyright © 2011-2018 Math Online Sweden AB. All Rights Reserved.